Posición aparente de un avión
De Laplace
(Nueva página: == Enunciado== Un observador escucha el ruido de un avión que se mueve con velocidad constante ''v'' (subsónica) a una altura ''h''. La trayectoria del avión pasa sobre la vertica...) |
(→Solución) |
||
| (Una edición intermedia no se muestra.) | |||
| Línea 4: | Línea 4: | ||
==Solución== | ==Solución== | ||
| + | [[Imagen:Posicion_avion_no_supersonico_esquema.gif|right]] | ||
| + | Escogemos como origen de tiempos el instante en el que el avión pasa por la vertical del observador, el eje | ||
| + | <math>X</math> paralelo a la dirección de movimiento del avión y el origen de coordenadas en la posición del | ||
| + | observador. Con esta elección, la posición del avión viene siempre dada por la expresión | ||
| + | <center> | ||
| + | <math> | ||
| + | x_a(t) = vt | ||
| + | </math> | ||
| + | </center> | ||
| + | donde <math>v</math> es la velocidad del avión. Supondremos que la velocidad es positiva y que el avión se | ||
| + | mueve hacia la derecha en la figura. | ||
| + | |||
| + | El observador mira en la dirección en que llega la onda sonora emitida por el avión. Pero como esta onda tarda | ||
| + | un cierto tiempo en recorrer la distancia entre el avión y él, cuando recibe la onda no mira hacia la | ||
| + | posición actual del avión, sino hacia la posición en que éste estaba cuando emitió la onda. | ||
| + | En el instante <math>t</math> la posición que el observador atribuye al avión es <math>x_o(t)</math>. La onda | ||
| + | emitida por el avión en ese instante tarda un tiempo <math>t_d</math> en llegar, que vale | ||
| + | <center> | ||
| + | <math> | ||
| + | t_d=\frac{d(t)}{c}=\frac{\sqrt{x_o^2(t)+h^2}}{c} | ||
| + | </math> | ||
| + | </center> | ||
| + | donde <math>c</math> es la velocidad de propagación del sonido. | ||
| + | En ese tiempo, el avión se ha seguido desplazando. Entonces, la diferencia entre la posición que el observador atribuye | ||
| + | al avión y su posición real es | ||
| + | <center> | ||
| + | <math> | ||
| + | x_o(t)-x_a(t)=vt_d=v\frac{\sqrt{x_o(t)^2+h^2}}{c} | ||
| + | </math> | ||
| + | </center> | ||
| + | Esta es una ecuación de segundo grado para <math>x_o(t)</math>. Reordenando resulta | ||
| + | <center> | ||
| + | <math> | ||
| + | (c^2-v^2)x_o^2-2c^2x_ax_o+c^2x_a^2-v^2h^2=0 | ||
| + | </math> | ||
| + | </center> | ||
| + | La solución es | ||
| + | <center> | ||
| + | <math> | ||
| + | x_o(t) = \frac{\displaystyle x_a(t)\pm\frac{v}{c}\sqrt{x_a^2(t)+h^2(1-v^2/c^2)}}{1-v^2/c^2} | ||
| + | </math> | ||
| + | </center> | ||
| + | Escogemos el signo negativo para la raíz, pues el avión parece estar más alejado de su posición real. El otro signo corresponde | ||
| + | al caso en el que el avión se mueve hacia la izquierda y <math>v</math> es negativa. Como <math>x_a(t)=vt</math>, queda | ||
| + | <center> | ||
| + | <math> | ||
| + | x_o(t) = \frac{\displaystyle vt-\frac{v}{c}\sqrt{v^2t^2+h^2(1-v^2/c^2)}}{1-v^2/c^2} | ||
| + | </math> | ||
| + | </center> | ||
| + | [[Imagen:Posicion_avion_no_supersonico_xa_xo.gif|right]] | ||
| + | A título de verificación, consideremos la siguiente situación. Cuando el avión pasa justo sobre el observador (<math>x_a=0</math>), la onda | ||
| + | que emite tarda un tiempo <math>t_0=h/c</math> en llegar al observador. Es decir, debería ocurrir que <math>x_o(t_0)=0</math>. | ||
| + | Sustiuyendo en la expresión anterior puede verificarse que es así. | ||
| + | |||
| + | La figura muestra la diferencia entre la posición real del avión y la percibida por el observador en función del tiempo. La | ||
| + | gráfica está dibujada con los valores <math>c=343</math> m/s, <math>v=100</math> m/s, <math>h=3</math> km. | ||
| + | |||
| + | Para calcular la velocidad que el observador atribuye al avión, debemos derivar <math>x_o(t)</math> respecto al tiempo | ||
| + | <center> | ||
| + | <math> | ||
| + | v_o(t)=\frac{\mathrm{d}x_o}{\mathrm{d}t}=\frac{v}{1-v^2/c^2}\left(1-\frac{v}{c}\frac{vt}{\sqrt{v^2t^2+h^2(1-v^2/c^2)}}\right) | ||
| + | </math> | ||
| + | </center> | ||
| + | El avión alejado y acercándose corresponde a <math>t\to-\infty</math>. En esta caso la velocidad tiende a | ||
| + | <center> | ||
| + | <math> | ||
| + | v_o(t\to-\infty)=\frac{v}{1-v^2/c^2}\left(1+\frac{v}{c}\right)=\frac{v}{1-v/c} | ||
| + | </math> | ||
| + | </center> | ||
| + | Cuando el avión está lejos y alejándos se tiene <math>t\to+\infty</math>. En este caso se tiene | ||
| + | <center> | ||
| + | <math> | ||
| + | v_o(t\to+\infty)=\frac{v}{1-v^2/c^2}\left(1-\frac{v}{c}\right)=\frac{v}{1+v/c} | ||
| + | </math> | ||
| + | </center> | ||
| + | Vemos que la velocidad aparente del avión es mayor que la real cuando se acerca y menor cuando se aleja, pues | ||
| + | <math>v<c</math> siempre. | ||
| + | [[Imagen:Posicion_avion_no_supersonico_vo_v.gif|right]] | ||
| + | La figura de la derecha representa el cociente de la velocidad medida por el observador y la velocidad real del avión. | ||
| + | Se han usado los mismos valores que en la gráfica anterior. Pueden observarse los dos límites cuando el avión está | ||
| + | lejos, acercándose y alejándose. Las dos velocidades coinciden cuando <math>v_o(t_0)=v</math>. El valor de <math>t_0</math> es | ||
| + | <center> | ||
| + | <math> | ||
| + | t_0=h/c | ||
| + | </math> | ||
| + | </center> | ||
| + | Este instante corresponde también al mínimo que se observa en la gráfica <math>x_a(t)-x_o(t)</math>, pues la derivada de | ||
| + | esta función es precisamente la diferencia de velocidades. Este tiempo corresponde a la situación que hemos considerado para | ||
| + | verificar el resultado anteriormente. | ||
| + | [[Categoría:Problemas de ondas sonoras]] | ||
última version al 13:12 4 may 2009
1 Enunciado
Un observador escucha el ruido de un avión que se mueve con velocidad constante v (subsónica) a una altura h. La trayectoria del avión pasa sobre la vertical del observador. Este torpe observador siempre mira en la dirección de la que viene el ruido. Para esta persona ¿cómo varía aparentemente la posición del avión con el tiempo? ¿Con qué velocidad se mueve aparentemente cuando se encuentra muy alejado acercándose? ¿Y cuando está muy lejos alejándose del observador?
2 Solución
Escogemos como origen de tiempos el instante en el que el avión pasa por la vertical del observador, el eje X paralelo a la dirección de movimiento del avión y el origen de coordenadas en la posición del observador. Con esta elección, la posición del avión viene siempre dada por la expresión
xa(t) = vt
donde v es la velocidad del avión. Supondremos que la velocidad es positiva y que el avión se mueve hacia la derecha en la figura.
El observador mira en la dirección en que llega la onda sonora emitida por el avión. Pero como esta onda tarda un cierto tiempo en recorrer la distancia entre el avión y él, cuando recibe la onda no mira hacia la posición actual del avión, sino hacia la posición en que éste estaba cuando emitió la onda. En el instante t la posición que el observador atribuye al avión es xo(t). La onda emitida por el avión en ese instante tarda un tiempo td en llegar, que vale
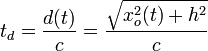
donde c es la velocidad de propagación del sonido. En ese tiempo, el avión se ha seguido desplazando. Entonces, la diferencia entre la posición que el observador atribuye al avión y su posición real es
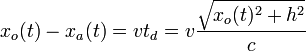
Esta es una ecuación de segundo grado para xo(t). Reordenando resulta
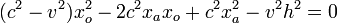
La solución es
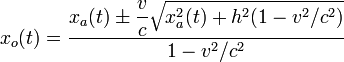
Escogemos el signo negativo para la raíz, pues el avión parece estar más alejado de su posición real. El otro signo corresponde al caso en el que el avión se mueve hacia la izquierda y v es negativa. Como xa(t) = vt, queda
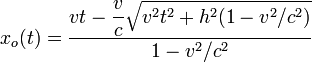
A título de verificación, consideremos la siguiente situación. Cuando el avión pasa justo sobre el observador (xa = 0), la onda que emite tarda un tiempo t0 = h / c en llegar al observador. Es decir, debería ocurrir que xo(t0) = 0. Sustiuyendo en la expresión anterior puede verificarse que es así.
La figura muestra la diferencia entre la posición real del avión y la percibida por el observador en función del tiempo. La gráfica está dibujada con los valores c = 343 m/s, v = 100 m/s, h = 3 km.
Para calcular la velocidad que el observador atribuye al avión, debemos derivar xo(t) respecto al tiempo
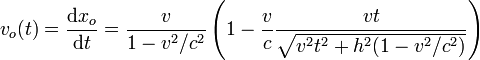
El avión alejado y acercándose corresponde a 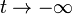 . En esta caso la velocidad tiende a
. En esta caso la velocidad tiende a
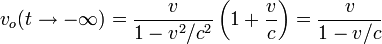
Cuando el avión está lejos y alejándos se tiene 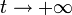 . En este caso se tiene
. En este caso se tiene
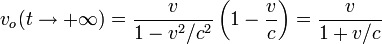
Vemos que la velocidad aparente del avión es mayor que la real cuando se acerca y menor cuando se aleja, pues v < c siempre.
La figura de la derecha representa el cociente de la velocidad medida por el observador y la velocidad real del avión. Se han usado los mismos valores que en la gráfica anterior. Pueden observarse los dos límites cuando el avión está lejos, acercándose y alejándose. Las dos velocidades coinciden cuando vo(t0) = v. El valor de t0 es
t0 = h / c
Este instante corresponde también al mínimo que se observa en la gráfica xa(t) − xo(t), pues la derivada de esta función es precisamente la diferencia de velocidades. Este tiempo corresponde a la situación que hemos considerado para verificar el resultado anteriormente.








