Superficies equiescalares
De Laplace
(Nueva página: ==Campos en tres dimensiones== Sin embargo, cuando se trata de una función de las tres coordenadas, la cosa se complica. Ya no disponemos de la tercera dimensión para hacer una grá...) |
(→Enlaces) |
||
| (25 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Campos en tres dimensiones== | ==Campos en tres dimensiones== | ||
| - | + | La [[Visualización de campos escalares en dos dimensiones|visualización de campos dependientes de dos coordenadas]] es relativamente sencilla | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | La forma más fructífera de representar los campos escalares funciones | + | Sin embargo, cuando se trata de una función de las tres coordenadas, la cosa se complica. Ya no disponemos de la tercera dimensión para hacer una gráfica de elevación, y cualquier representación bidimensional se referirá a una sección del espacio. |
| - | de | + | |
| - | + | ==Definición== | |
| - | equiescalares | + | La forma más fructífera de representar los campos escalares funciones de las tres coordenadas es con ayuda de las ''superficies equiescalares'' o ''equipotenciales'', definida cada una de ellas como el conjunto de los puntos en que el campo escalar tiene un cierto valor fijado: |
| - | como el conjunto de los puntos en que el campo escalar tiene un cierto | + | |
| - | valor fijado | + | <center><math>\phi(x,y,z) = k\,</math></center> |
| - | + | ||
| - | \phi(x,y,z) = k | + | Una propiedad importante de las superficies equipotenciales es que no se cortan entre sí, dado que el campo posee un solo valor en cada punto. |
| - | \ | + | |
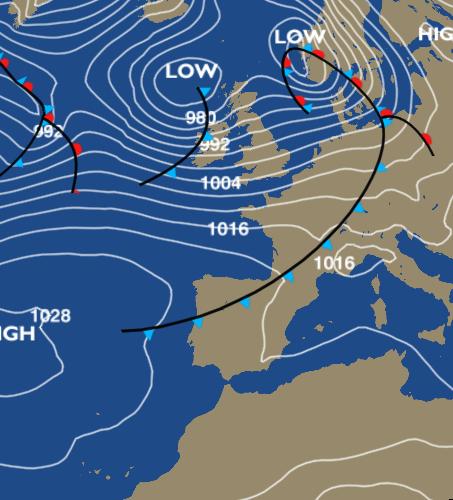
| - | Una propiedad importante de las superficies equipotenciales es que no | + | [[Imagen:isobaras.jpg|right]]Un ejemplo habitual es el de las ''isobaras'' de un mapa del tiempo. |
| - | se cortan entre sí, dado que el campo posee un solo valor en cada | + | Sin embargo, este mapa es sólo una representación de las líneas correspondientes a la presión a nivel del mar, <math>p = p(x,y)\,</math>. Una verdadera representación de las isobaras debería incluir superficies en un volumen tridimensional. Estas superficies, en el caso de la presión, se envolverían unas a otras como capas de una cebolla. |
| - | punto. | + | |
| + | Para casos más generales, las superficies equipotenciales pueden tener formas muy complejas. Por ejemplo, en el caso del campo escalar | ||
| + | |||
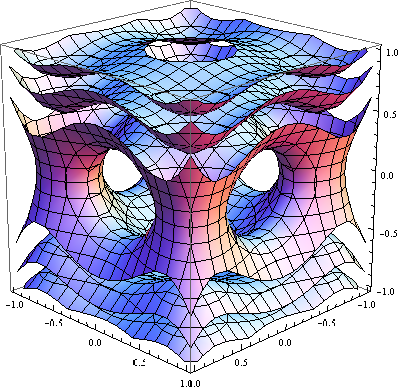
| + | <center><math>\phi = -x^4+x^2-y^4+y^2+z^2</math></center> | ||
| + | |||
| + | resultan superficies como estas: | ||
| + | |||
| + | [[Imagen:equiescalares.png|left]] | ||
| + | |||
| + | Normalmente, en muy pocos casos puede uno ''imaginar'' la forma de las superficies equipotenciales. Eso no impide usarlas como herramientas por sus propiedades geométricas. Lo veremos en su aplicación al [[potencial eléctrico]] y su [[gradiente]], el [[campo electrostático]]. | ||
| + | |||
| + | ==Enlaces== | ||
| + | * '''Siguiente:''' [[Ejemplos de superficies equiescalares]] | ||
| + | * '''Anterior:''' [[Visualización de campos escalares en dos dimensiones]] | ||
| + | |||
| + | [[Categoría:Campos escalares y vectoriales|30]] | ||
última version al 17:14 2 dic 2007
1 Campos en tres dimensiones
La visualización de campos dependientes de dos coordenadas es relativamente sencilla
Sin embargo, cuando se trata de una función de las tres coordenadas, la cosa se complica. Ya no disponemos de la tercera dimensión para hacer una gráfica de elevación, y cualquier representación bidimensional se referirá a una sección del espacio.
2 Definición
La forma más fructífera de representar los campos escalares funciones de las tres coordenadas es con ayuda de las superficies equiescalares o equipotenciales, definida cada una de ellas como el conjunto de los puntos en que el campo escalar tiene un cierto valor fijado:
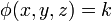
Una propiedad importante de las superficies equipotenciales es que no se cortan entre sí, dado que el campo posee un solo valor en cada punto.
Sin embargo, este mapa es sólo una representación de las líneas correspondientes a la presión a nivel del mar,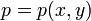 
. Una verdadera representación de las isobaras debería incluir superficies en un volumen tridimensional. Estas superficies, en el caso de la presión, se envolverían unas a otras como capas de una cebolla.
Para casos más generales, las superficies equipotenciales pueden tener formas muy complejas. Por ejemplo, en el caso del campo escalar
resultan superficies como estas:
Normalmente, en muy pocos casos puede uno imaginar la forma de las superficies equipotenciales. Eso no impide usarlas como herramientas por sus propiedades geométricas. Lo veremos en su aplicación al potencial eléctrico y su gradiente, el campo electrostático.
