Problemas de máquinas térmicas (GIOI)
De Laplace
(→Refrigerador alimentado por máquina térmica) |
|||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 27: | Línea 27: | ||
<center>[[Archivo:Esquema-ciclo-otto.png]]</center> | <center>[[Archivo:Esquema-ciclo-otto.png]]</center> | ||
| - | + | # ¿Cuál es el rendimiento teórico del motor? | |
| - | + | # ¿Cuáles son las presiones, volúmenes y temperaturas e los estados A, B, C y D del ciclo? | |
| - | + | # ¿Cuánto vale el calor y el trabajo en cada uno de los 4 procesos? ¿Son de entrada o de salida? | |
| - | + | # ¿Cuánto vale el trabajo neto de salida en el ciclo? | |
| - | + | # Considerando el trabajo que se realiza por segundo, ¿cuánto vale la potencia de este motor? ¿Cuánto vale esta potencia en CV (1 CV=0.7457 kW)? | |
[[Caso práctico de ciclo Otto ideal (GIOI)|'''Solución''']] | [[Caso práctico de ciclo Otto ideal (GIOI)|'''Solución''']] | ||
| Línea 39: | Línea 39: | ||
<center>[[Archivo:Ejemplo-ciclo-Carnot.png|300px]]</center> | <center>[[Archivo:Ejemplo-ciclo-Carnot.png|300px]]</center> | ||
| - | + | # Calcule la presión, volumen y temperatura de los estados A, B, C y D. | |
| - | + | # Calcule el calor que entra o sale en cada uno de los cuatro pasos. | |
| - | + | # Halle el trabajo neto de salida a lo largo de un ciclo. | |
| - | + | # Calcule el rendimiento de este ciclo. | |
| + | [[Caso práctico de ciclo de Carnot (GIOI)|'''Solución''']] | ||
| + | |||
| + | =={{nivel|3}} Refrigerador de Carnot== | ||
| + | Se tiene un refrigerador que funciona con un ciclo de Carnot inverso (es decir, recorrido en sentido contrario) entre las temperaturas <math>T_C</math> y <math>T_F</math>. ¿Cuánto vale su COP<sub>R</sub> en función de estas dos temperaturas? ¿Y si fuera una bomba de calor, cuál sería su COP<sub>BC</sub>? | ||
| + | |||
| + | [[Refrigerador de Carnot (GIOI)|'''Solución''']] | ||
| + | |||
| + | =={{nivel|4}} Refrigerador por ciclo Brayton== | ||
| + | Se construye un refrigerador que funciona mediante un ciclo Brayton inverso de gas ideal (γ = 1.4). Este refrigerador debe mantener fría una cámara a 270 K estando el exterior a 300 K. Inicialmente el gas ocupa 0.45 L y se encuentra a la temperatura de la cámara frigorífica y a una presión <math>p_A=50 \,\mathrm{kPa}</math>. El compresor eleva su presión a <math>p_B=100\,\mathrm{ kPa}</math> mediante una compresión adiabática. Entonces se deja que el gas se enfríe a presión constante hasta que llegue a la temperatura exterior. Una vez alcanzada esta temperatura, se expande de nuevo de forma adiabática hasta que llega a la presión inicial. Se deja entonces que se caliente a presión constante hasta que llega a la temperatura de la cámara, cerrando el ciclo. | ||
| + | |||
| + | <center>[[Archivo:Refrigerador_brayton.png|300px]]</center> | ||
| + | # Calcule la presión, volumen y temperatura de los cuatros estados A, B, C y D. | ||
| + | # Halle el calor que entra o sale en cada uno de los pasos. | ||
| + | # Calcule el trabajo neto que entra en cada ciclo. | ||
| + | # Halle el COPR de este refrigerador. | ||
| + | |||
| + | [[Refrigerador por ciclo Brayton (GIOI)|'''Solución''']] | ||
| + | |||
| + | ==Refrigerador alimentado por máquina térmica== | ||
| + | Para alimentar un refrigerador que tiene un cierto COP<sub>R</sub> en una casa en el campo se usa un grupo electrógeno que es una máquina térmica con rendimiento η. | ||
| + | # {{nivel|2}} Si definimos el rendimiento del conjunto como la proporción entre el calor que extrae del interior de la cámara frigorífica y el calor que consume la máquina térmica, ¿cuánto vale este rendimiento en función de las dos cantidades anteriores? | ||
| + | # {{nivel|2}} Si el calor que extrae por segundo es <math>\dot{Q}_\mathrm{in}^R</math>, ¿cuánto calor de desecho produce por segundo? | ||
| + | # {{nivel|3}} Supongamos que esta máquina térmica sigue un ciclo Otto ideal con relación de compresión <math>r=8</math>, mientras que el refrigerador sigue un ciclo Brayton inverso con <math>r_p=2</math>, ¿cuánto vale el rendimiento del conjunto? | ||
| + | # {{nivel|2}} Si para este caso el calor absorbido por segundo es 1kW, ¿cuánto calor de desecho produce por segundo? | ||
| + | # {{nivel|2}} Si para este caso el grupo electrógeno funciona con gasolina, que produce calor a un ritmo de 45 MJ/kg (poder calorífico) y la densidad de la gasolina es de 0.73 kg/L, ¿cuántos litros de gasolina consume en un día? | ||
| + | |||
| + | [[Refrigerador alimentado por máquina térmica (GIOI)|'''Solución''']] | ||
última version al 09:38 17 may 2021
1 
Rendimiento de una máquina térmica
Una máquina térmica opera a 300 rpm de manera que en cada ciclo absorbe 4000 J de una caldera y expulsa 2400 J al ambiente. Si para funcionar la máquina requiere 200 J de potencia eléctrica de entrada, ¿cuánto vale el trabajo de salida? ¿Cuánto vale el rendimiento de la máquina? Si consideramos los flujos de calor y de trabajo, ¿cuánto vale el flujo de trabajo neto de salida (trabajo neto de salida por segundo)?
2 Rendimiento de un refrigerador y de una bomba de calor
Un aparato de aire acondicionado extrae 4 kW de calor de una habitación, que es el calor que entra por las ventanas y paredes cuando la temperatura interior es de 23 °C y la exterior es de 38 °C, consumiendo una potencia de 1 kW eléctrico. ¿Cuánto vale el COPR del refrigerador? Supongamos que este aparato de aire acondicionado tiene inverter, de forma que también funciona como bomba de calor. ¿Cuánto vale el COPBC de esta bomba? Si la temperatura exterior es de 8 °C de forma que el flujo de calor es el opuesto al del verano, ¿Qué consumo eléctrico tiene la bomba?
3 
Dos máquinas térmicas puestas en serie
Una central eléctrica de ciclo combinado está formada por dos máquinas térmicas puestas en serie, de manera que el calor de desecho de la primera se emplea para alimentar la segunda. Si el rendimiento de la primera vale η1 y el de la segunda vale η2, ¿cuánto vale el rendimiento del conjunto? Suponga que, en un caso concreto la primera máquina toma 600 MW de calor de una caldera y tiene un rendimiento de un 40%, mientras que la segunda tiene un rendimiento de 1/3. ¿Cuál es la potencia eléctrica que produce cada una de las máquinas y cuál es la del conjunto?
4 Dos refrigeradores en serie
Para conseguir refrigerar a muy bajas temperaturas se colocan dos refrigeradores en serie. El primero, que tiene un COPR1 extrae el calor de la sustancia desde la temperatura TF hasta una temperatura intermedia TM. El segundo, que tiene un COPR2 toma el calor desde TM y lo expulsa al ambiente a TC. ¿Cuánto vale el COPR del conjunto? Supongamos el caso particular COPR1 = 4 y COPR2 = 3. Si el segundo refrigerador consume 1 kW de potencia eléctrica, ¿cuánto consume el conjunto? ¿Cuánto calor extrae de la sustancia y cuánto expulsa al ambiente?
5 
Caso práctico de ciclo Otto ideal
Un motor de gasolina se puede modelar mediante un ciclo Otto ideal (γ = 1.4). Supongamos que el motor posee turbocompresor de manera que la mezcla entra a 200 kPa y 320 K. La cilindrada del motor es de 1400 cm³ y la relación de compresión es de 8. En la combustión la temperatura del gas alcanza los 1500 K. Supongamos que el motor opera a 3000 rpm (que teniendo en cuenta que se trata de un motor de 4 tiempos equivale a 1500 ciclos/min).
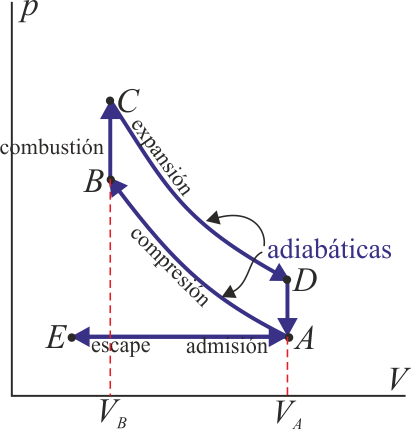
- ¿Cuál es el rendimiento teórico del motor?
- ¿Cuáles son las presiones, volúmenes y temperaturas e los estados A, B, C y D del ciclo?
- ¿Cuánto vale el calor y el trabajo en cada uno de los 4 procesos? ¿Son de entrada o de salida?
- ¿Cuánto vale el trabajo neto de salida en el ciclo?
- Considerando el trabajo que se realiza por segundo, ¿cuánto vale la potencia de este motor? ¿Cuánto vale esta potencia en CV (1 CV=0.7457 kW)?
6 Caso práctico de ciclo de Carnot
Se tiene un ciclo de Carnot ideal de un gas ideal (γ = 1.4) en el cual la temperatura del foco caliente vale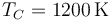 
y la del foco frío es 
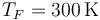. Antes de la compresión adiabática el volumen es 
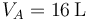y su presión es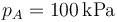 
- Calcule la presión, volumen y temperatura de los estados A, B, C y D.
- Calcule el calor que entra o sale en cada uno de los cuatro pasos.
- Halle el trabajo neto de salida a lo largo de un ciclo.
- Calcule el rendimiento de este ciclo.
7 Refrigerador de Carnot
Se tiene un refrigerador que funciona con un ciclo de Carnot inverso (es decir, recorrido en sentido contrario) entre las temperaturas TC y TF. ¿Cuánto vale su COPR en función de estas dos temperaturas? ¿Y si fuera una bomba de calor, cuál sería su COPBC?
8 
Refrigerador por ciclo Brayton
Se construye un refrigerador que funciona mediante un ciclo Brayton inverso de gas ideal (γ = 1.4). Este refrigerador debe mantener fría una cámara a 270 K estando el exterior a 300 K. Inicialmente el gas ocupa 0.45 L y se encuentra a la temperatura de la cámara frigorífica y a una presión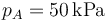 
. El compresor eleva su presión a 
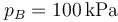mediante una compresión adiabática. Entonces se deja que el gas se enfríe a presión constante hasta que llegue a la temperatura exterior. Una vez alcanzada esta temperatura, se expande de nuevo de forma adiabática hasta que llega a la presión inicial. Se deja entonces que se caliente a presión constante hasta que llega a la temperatura de la cámara, cerrando el ciclo.
- Calcule la presión, volumen y temperatura de los cuatros estados A, B, C y D.
- Halle el calor que entra o sale en cada uno de los pasos.
- Calcule el trabajo neto que entra en cada ciclo.
- Halle el COPR de este refrigerador.
9 Refrigerador alimentado por máquina térmica
Para alimentar un refrigerador que tiene un cierto COPR en una casa en el campo se usa un grupo electrógeno que es una máquina térmica con rendimiento η.
- Si definimos el rendimiento del conjunto como la proporción entre el calor que extrae del interior de la cámara frigorífica y el calor que consume la máquina térmica, ¿cuánto vale este rendimiento en función de las dos cantidades anteriores?
- Si el calor que extrae por segundo es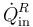
, ¿cuánto calor de desecho produce por segundo?
- Supongamos que esta máquina térmica sigue un ciclo Otto ideal con relación de compresión r = 8, mientras que el refrigerador sigue un ciclo Brayton inverso con rp = 2, ¿cuánto vale el rendimiento del conjunto?
- Si para este caso el calor absorbido por segundo es 1kW, ¿cuánto calor de desecho produce por segundo?
- Si para este caso el grupo electrógeno funciona con gasolina, que produce calor a un ritmo de 45 MJ/kg (poder calorífico) y la densidad de la gasolina es de 0.73 kg/L, ¿cuántos litros de gasolina consume en un día?
