Cinco resistencias iguales
De Laplace
| (14 ediciones intermedias no se muestran.) | |||
| Línea 23: | Línea 23: | ||
Esto hace que entre C y D no haya diferencia de potencial y por tanto, por la rama central no circule corriente. | Esto hace que entre C y D no haya diferencia de potencial y por tanto, por la rama central no circule corriente. | ||
| + | |||
| + | Esto puede verse quizá de forma más evidente mediante este esquema equivalente al del enunciado | ||
| + | |||
| + | <center>[[Archivo:5-resistencias-04.png|437px]]</center> | ||
| + | |||
El sistema se reduce entonces a dos ramas en paralelo, ya que la resistencia central es como si no estuviera. La rama superior, pasando por D, tiene resistencia 2R, y la rama inferior, pasando por C, tiene también resistencia 2R, siendo <math>R = 12\,\Omega</math>. | El sistema se reduce entonces a dos ramas en paralelo, ya que la resistencia central es como si no estuviera. La rama superior, pasando por D, tiene resistencia 2R, y la rama inferior, pasando por C, tiene también resistencia 2R, siendo <math>R = 12\,\Omega</math>. | ||
| Línea 47: | Línea 52: | ||
Para ir de A (entrada de la corriente) a C (salida de la corriente) hay dos caminos en paralelo. Uno va directo y tiene resistencia R. El otro va pasando por D y está formado por dos elementos en serie: una resistencia R y una asociación en paralelo de una resistencia R y una resistencia 2R. El esquema se puede reescribir de esta forma: | Para ir de A (entrada de la corriente) a C (salida de la corriente) hay dos caminos en paralelo. Uno va directo y tiene resistencia R. El otro va pasando por D y está formado por dos elementos en serie: una resistencia R y una asociación en paralelo de una resistencia R y una resistencia 2R. El esquema se puede reescribir de esta forma: | ||
| - | <center>[[Archivo:5-resistencias-02.png| | + | <center>[[Archivo:5-resistencias-02.png|515px]]</center> |
La resistencia equivalente de la rama superior es | La resistencia equivalente de la rama superior es | ||
| Línea 59: | Línea 64: | ||
siendo la corriente que entra por A | siendo la corriente que entra por A | ||
| - | <center><math>I_A=\frac{V_A-V_C}{R_\mathrm{eq}}=\frac{24\,\mathrm{mV}}{7.5\,Omega}= | + | <center><math>I_A=\frac{V_A-V_C}{R_\mathrm{eq}}=\frac{24\,\mathrm{mV}}{7.5\,\Omega}=3.2\,\mathrm{mA}</math></center> |
y, para los otros dos terminales | y, para los otros dos terminales | ||
| - | <center><math>I_C=-1. | + | <center><math>I_C=-3.2\,\mathrm{mA}\qquad\qquad I_B=0\,\mathrm{mA}</math></center> |
| + | |||
| + | ==Tercer caso== | ||
| + | Al poner los terminales B y C a tierra, estamos cortocircuitando la resistencia que entre estos dos nodos, ya que al estar al mismo potencial ya no circula corriente por ella. | ||
| + | |||
| + | Ahora el sistema se reduce a | ||
| + | |||
| + | <center>[[Archivo:5-resistencias-03.png|515px]]</center> | ||
| + | |||
| + | (obsérvese que aunque B y C están en puntos distintos, entre ellos no hay resistencia alguna, por lo que están al mismo potencial) | ||
| + | |||
| + | La resistencia equivalente de la rama superior es ahora | ||
| + | |||
| + | <center><math>R_2 = R + \frac{R\cdot R}{R+R} = R+ \frac{1}{2}R=\frac{3}{2}R=18\,\Omega</math></center> | ||
| + | |||
| + | y la del conjunto | ||
| + | |||
| + | <center><math>R_\mathrm{eq}=\frac{(3R/2)R}{(3R/2)+R}=\frac{3}{5}R=7.2\,\Omega</math></center> | ||
| + | |||
| + | siendo la corriente que entra por A | ||
| + | |||
| + | <center><math>I_A=\frac{V_A-V_C}{R_\mathrm{eq}}=\frac{24\,\mathrm{mV}}{7.2\,\Omega}=3.33\,\mathrm{mA}</math></center> | ||
| + | |||
| + | La intensidad de corriente que sale por B y la que sale por C son diferentes, ya que están conectados de distinta forma a A. Según hemos dicho, desde A salen dos ramas en paralelo: una con resistencia R y una con resistencia <math>R_2</math>. La corriente se reparte entre ambas en la forma | ||
| + | |||
| + | <center><math>I_1=\frac{R_2}{R+R_2}I=\frac{3R/2}{3R/2+R}I=\frac{3}{5}I=2.00\,\mathrm{mA}</math></center> | ||
| + | |||
| + | y | ||
| + | |||
| + | <center><math>I_2=\frac{R}{R+R_2}I=\frac{R}{3R/2+R}I=\frac{2}{5}I=1.33\,\mathrm{mA}</math></center> | ||
| + | |||
| + | A su vez, esta corriente se divide en dos iguales, una por cada rama en paralelo. | ||
| + | |||
| + | <center><math>I_{2a}=I_{2b}=\frac{I_2}{2}=0.67\,\mathrm{mA}</math></center> | ||
| + | |||
| + | La corriente que sale por B es una de estas dos mitades | ||
| + | |||
| + | <center><math>I_B = -0.67\,\mathrm{mA}</math></center> | ||
| + | |||
| + | mientras que por C sale la otra mitad más la que va directamente desde A a C | ||
| + | |||
| + | <center><math>I_C = -\left(I_1+\frac{I_2}{2}\right)=-2.67\,\mathrm{mA}</math></center> | ||
| + | |||
| + | ==Solución general== | ||
| + | ===Empleando la 1ª let de Kirchhoff y la ley de Ohm=== | ||
| + | Para el caso de que los tres voltajes, pero también para los caso anteriores, es más interesante hallar una solución general. Tenemos cinco resistencias y por cada una circulará una cierta corriente, cumpliéndose en cada una la ley de Ohm. | ||
| + | |||
| + | <center>[[Archivo:5-resistencias-05.png|437px]]</center> | ||
| + | |||
| + | Según el esquema de la figura, aplicando aquí la 1ª ley de Kirchhoff para cada uno de los cuatro nodos queda | ||
| + | |||
| + | <center><math>I_A-I_1-I_3=0\qquad\qquad I_2+I_4+I_B=0\qquad\qquad I_1+I_5+I_C-I_4=0\qquad\qquad I_1-I_2-I_5=0</math></center> | ||
| + | |||
| + | siendo <math>I_A</math> la intensidad que entra por A, y análogamente para <math>I_B</math> e <math>I_C</math>. Por D no entra corriente. | ||
| + | |||
| + | El criterio es que se suman todas las corrientes que llegan a un nodo, precediéndolas de un signo - si salen de él. Esto no presupone que el resultado de cada una de estas intensidades vaya a ser un número positivo. Por ejemplo, necesariamente en B alguna de las tres intensidades debe resultar negativa. | ||
| + | |||
| + | Cada una de estas intensidades se relaciona con la diferencia de potencial entre sus extremos mediante la ley de Ohm: | ||
| + | |||
| + | <center><math>I_1=\frac{V_A-V_D}{R}\qquad\qquad I_2=\frac{V_D-V_B}{R}\qquad\qquad I_3=\frac{V_A-V_C}{R}</math></center> | ||
| + | | ||
| + | <center><math>I_4=\frac{V_C-V_B}{R}\qquad\qquad I_5=\frac{V_D-V_C}{R}</math></center> | ||
| + | |||
| + | Con este sistema ya es suficiente para analizar cada caso, pero podemos dar una solución general para <math>I_A</math>, <math>I_B</math> e <math>I_C</math> en función de <math>V_A</math>, <math>V_B</math> y <math>V_C</math>. | ||
| + | |||
| + | Sustituimos la ley de Ohm en la ley de Kirchhoff para el nodo D y obtenemos el voltaje de este nodo | ||
| + | |||
| + | <center><math>\frac{V_A-V_D}{R}-\frac{V_D-V_B}{R}-\frac{V_D-V_C}{R}=0\qquad\Rightarrow\qquad V_D=\frac{V_A+V_B+V_C}{3}</math></center> | ||
| + | |||
| + | y llevamos este resultado al resto de nodos. Sustituimos en la ecuación para el nodo A | ||
| + | |||
| + | <center><math>I_A = I_1+I_3=\frac{V_A-V_D}{R}+\frac{V_A-V_C}{R}=\frac{5V_A-V_B-4V_C}{3R}</math></center> | ||
| + | |||
| + | Sustituimos en la del nodo B | ||
| + | |||
| + | <center><math>I_B = -I_2-I_4=\frac{-V_A+5V_B-4V_C}{3R}</math></center> | ||
| + | |||
| + | y en la del C | ||
| + | |||
| + | <center><math>I_C=-I_3-I_5+I_4=\frac{-4V_A-4V_B+8V_C}{3R}</math></center> | ||
| + | |||
| + | Este resultado se puede escribir en la forma matricial | ||
| + | |||
| + | <center><math>\left(\begin{matrix}I_A\\I_B\\I_C\end{matrix}\right)=\frac{1}{3R}\left(\begin{matrix}5&-1&-4\\-1&5&-4\\-4&-4&8\end{matrix}\right)\cdot\left(\begin{matrix}V_A\\V_B\\V_C\end{matrix}\right)</math></center> | ||
| + | |||
| + | ===Empleando las dos leyes de Kirchhoff=== | ||
| + | Alternativamente, podemos llegar a estas ecuaciones aplicando la dos leyes de Kirchhoff. En ese caso debemos incluir las fuentes como parte del sistema, resultando un conjunto de cuatro mallas: | ||
| + | |||
| + | <center>[[Archivo:5-resistencias-05.png|500px]]</center> | ||
| + | |||
| + | La ley de Kirchhoff de los nodos ya la hemos expuesto | ||
| + | |||
| + | <center><math>I_A-I_1-I_3=0\qquad\qquad I_2+I_4+I_B=0\qquad\qquad I_1+I_5+I_C-I_4=0\qquad\qquad I_1-I_2-I_5=0</math></center> | ||
| + | |||
| + | y para las mallas resultan las cuatro ecuaciones | ||
| + | |||
| + | <center><math>I_3R-I_5R-I_1R=0\qquad\qquad I_4R-I_2R+I_5R=0\qquad\qquad -V_C-I_3R+V_A=0\qquad\qquad -V_B-I_4R+V_C=0</math></center> | ||
| + | |||
| + | De la 3ª y la 4ª es inmediato que | ||
| + | |||
| + | <center><math>I_3=\frac{V_A-V_C}{R}\qquad\qquad I_4=\frac{V_C-V_B}{R}</math></center> | ||
| + | |||
| + | Con las otras dos y con la 1ª ley para el nodo D llegamos a que | ||
| + | |||
| + | <center><math>I_1=\frac{2V_A-V_B-V_C}{3R}\qquad \qquad I_2=\frac{-V_A+2V_B-V_C}{3R}\qquad\qquad I_5=\frac{V_A+V_B-2V_C}{3R}</math></center> | ||
| + | |||
| + | y con las leyes de Kirchhoff para los nodos A, B y C reobtenemos la solución matricial ya conocida. | ||
| + | |||
| + | |||
| + | |||
| + | Veamos de nuevo cada uno de los casos que hemos resuelto ya | ||
| + | |||
| + | ===Primer caso=== | ||
| + | En la primera situación tenemos | ||
| + | |||
| + | <center><math>V_A=V_0\qquad\qquad V_B=0\qquad\qquad I_C = 0</math></center> | ||
| + | |||
| + | No conocemos <math>I_A</math>, <math>I_B</math> y <math>V_C</math>. Esto nos da el sistema de ecuaciones | ||
| + | |||
| + | <center><math>I_A=\frac{5V_0-4V_C}{3R}\qquad\qquad I_B = \frac{-V_0-4V_C}{3R}\qquad\qquad 0 = \frac{-4V_0+8V_C}{3R}</math></center> | ||
| + | |||
| + | De la última resulta | ||
| + | |||
| + | <center><math>V_C = \frac{V_0}{2}=12\,\mathrm{mV}</math></center> | ||
| + | |||
| + | y sustituyendo en las otras dos | ||
| + | |||
| + | <center><math>I_A=\frac{5V_0-4(V_0/2)}{3R}=\frac{V_0}{R}=2\,\mathrm{mA}</math></center> | ||
| + | |||
| + | y | ||
| + | |||
| + | <center><math>I_B=\frac{-V_0-4(V_0/2)}{3R}=-\frac{V_0}{R}=-2\,\mathrm{mA}</math></center> | ||
| + | |||
| + | ===Segundo caso=== | ||
| + | En la segunda situación tenemos | ||
| + | |||
| + | <center><math>V_A=V_0\qquad\qquad I_B=0\qquad\qquad V_C = 0</math></center> | ||
| + | |||
| + | No conocemos <math>I_A</math>, <math>V_B</math> e <math>I_C</math>. Esto nos da el sistema de ecuaciones | ||
| + | |||
| + | <center><math>I_A=\frac{5V_0-V_B}{3R}\qquad\qquad 0 = \frac{-V_0+5V_B}{3R}\qquad\qquad I_C = \frac{-4V_0-4V_B}{3R}</math></center> | ||
| + | |||
| + | De la segunda resulta | ||
| + | |||
| + | <center><math>V_B= \frac{V_0}{5}=4.8\,\mathrm{mV}</math></center> | ||
| + | |||
| + | y sustituyendo en las otras dos | ||
| + | |||
| + | <center><math>I_A=\frac{5V_0-(V_0/5)}{3R}=\frac{8V_0}{5R}=3.2\,\mathrm{mA}</math></center> | ||
| + | |||
| + | y | ||
| + | |||
| + | <center><math>I_C=\frac{-4V_0-4(V_0/5)}{3R}=-\frac{8V_0}{5R}=-3.2\,\mathrm{mA}</math></center> | ||
| + | |||
| + | ===Tercer caso=== | ||
| + | El tercer caso es ahora más sencillo que los dos anteriores, ya que nos dan los tres voltajes | ||
| + | |||
| + | <center><math>V_A=V_0\qquad\qquad V_B=0\qquad\qquad V_C = 0</math></center> | ||
| + | |||
| + | con lo que basta con sustituir | ||
| + | |||
| + | <center><math>\left(\begin{matrix}I_A\\I_B\\I_C\end{matrix}\right)=\frac{1}{3R}\left(\begin{matrix}5&-1&-4\\-1&5&-4\\-4&-4&8\end{matrix}\right)\cdot\left(\begin{matrix}V_0\\0\\0\end{matrix}\right)=\frac{V_0}{3R}\left(\begin{matrix}5\\-1\\-4\end{matrix}\right)=\left(\begin{matrix}3.33\\-0.67\\-2.67\end{matrix}\right)</math></center> | ||
| + | |||
| + | ==Cuarto caso== | ||
| + | Una vez que tenemos la solución general, es inmediata su aplicación al cuarto caso | ||
| + | |||
| + | <center><math>\left(\begin{matrix}I_A\\I_B\\I_C\end{matrix}\right)=\frac{1}{36}\left(\begin{matrix}5&-1&-4\\-1&5&-4\\-4&-4&8\end{matrix}\right)\cdot\left(\begin{matrix}24\\6\\0\end{matrix}\right)\mathrm{mA}=\left(\begin{matrix}3.17\\0.17\\-3.33\end{matrix}\right)\mathrm{mA}</math></center> | ||
| + | |||
| + | ==Quinto caso== | ||
| + | De la misma manera se aplica al 5º | ||
| + | |||
| + | <center><math>\left(\begin{matrix}I_A\\I_B\\I_C\end{matrix}\right)=\frac{1}{36}\left(\begin{matrix}5&-1&-4\\-1&5&-4\\-4&-4&8\end{matrix}\right)\cdot\left(\begin{matrix}24\\-24\\0\end{matrix}\right)\mathrm{mA}=\left(\begin{matrix}4\\-4\\0\end{matrix}\right)\mathrm{mA}</math></center> | ||
| + | |||
| + | En este caso no entra ni sale corriente por el nodo C porque es análogo al primero de los casos que consideramos, con el nodo C en el voltaje medio entre A y B. | ||
| + | |||
| + | ==Sexto caso== | ||
| + | Por último tenemos | ||
| + | |||
| + | <center><math>\left(\begin{matrix}I_A\\I_B\\I_C\end{matrix}\right)=\frac{1}{36}\left(\begin{matrix}5&-1&-4\\-1&5&-4\\-4&-4&8\end{matrix}\right)\cdot\left(\begin{matrix}24\\0\\-24\end{matrix}\right)\mathrm{mA}=\left(\begin{matrix}6\\2\\-8\end{matrix}\right)\mathrm{mA}</math></center> | ||
última version al 22:53 16 abr 2020
Contenido |
1 Enunciado
Dado el sistema de resistencias de la figura, calcule la intensidad de corriente que entra por el extremo A en los siguientes casos:

-
 En A se conecta una fuente de 24mV, C se deja abierto y B se conecta a tierra.
En A se conecta una fuente de 24mV, C se deja abierto y B se conecta a tierra.
-
 En A se conecta una fuente de 24mV, B se deja abierto y C se conecta a tierra.
En A se conecta una fuente de 24mV, B se deja abierto y C se conecta a tierra.
-
 En A se conecta una fuente de 24mV, B y C se conectan a tierra.
En A se conecta una fuente de 24mV, B y C se conectan a tierra.
-
 En A se conecta una fuente de 24mV, en C una de 6mV y B se conecta a tierra.
En A se conecta una fuente de 24mV, en C una de 6mV y B se conecta a tierra.
-
 En A se conecta una fuente de 24mV, en B una de −24mV y C se conecta a tierra.
En A se conecta una fuente de 24mV, en B una de −24mV y C se conecta a tierra.
-
 En A se conecta una fuente de 24mV, en C una de −24mV y B se conecta a tierra.
En A se conecta una fuente de 24mV, en C una de −24mV y B se conecta a tierra.
2 Introducción
Este problema se puede resolver de forma general, dando como resultado una expresión matricial para las corrientes que entran por A, B y C en función de los voltajes de estos nodos. Más adelante se describe esta solución general, aplicable a todos los apartados del problema.
Aparte de este caso general, muchos casos particulares pueden simplificarse aplicando asociaciones en serie y en paralelo de resistencias.
3 Primer caso
En el primer caso, el nodo C está abierto, es decir, no tiene fuente conectada, por lo que por C no entra ni sale corriente.
En este caso, al ser todas las resistencias iguales y tener simetría, el voltaje en el nodo C será la media entre el del A y el B.
Lo mismo ocurre con el nodo D, que sería el superior.
Esto hace que entre C y D no haya diferencia de potencial y por tanto, por la rama central no circule corriente.
Esto puede verse quizá de forma más evidente mediante este esquema equivalente al del enunciado

El sistema se reduce entonces a dos ramas en paralelo, ya que la resistencia central es como si no estuviera. La rama superior, pasando por D, tiene resistencia 2R, y la rama inferior, pasando por C, tiene también resistencia 2R, siendo 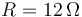 .
.
La resistencia equivalente del conjunto es

y por tanto la intensidad que entra por A (y sale por B) vale
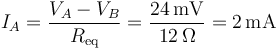
y, para los otros dos terminales
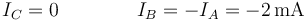
4 Segundo caso
En el segundo caso tenemos
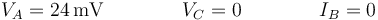
Este caso también se puede reducir a asociaciones en serie y en paralelo, aunque ya no hay simetría.
Para ir de A (entrada de la corriente) a C (salida de la corriente) hay dos caminos en paralelo. Uno va directo y tiene resistencia R. El otro va pasando por D y está formado por dos elementos en serie: una resistencia R y una asociación en paralelo de una resistencia R y una resistencia 2R. El esquema se puede reescribir de esta forma:

La resistencia equivalente de la rama superior es
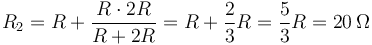
de manera que la resistencia equivalente del conjunto es
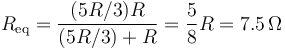
siendo la corriente que entra por A
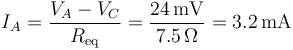
y, para los otros dos terminales

5 Tercer caso
Al poner los terminales B y C a tierra, estamos cortocircuitando la resistencia que entre estos dos nodos, ya que al estar al mismo potencial ya no circula corriente por ella.
Ahora el sistema se reduce a

(obsérvese que aunque B y C están en puntos distintos, entre ellos no hay resistencia alguna, por lo que están al mismo potencial)
La resistencia equivalente de la rama superior es ahora
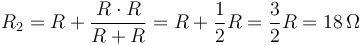
y la del conjunto
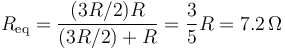
siendo la corriente que entra por A
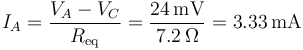
La intensidad de corriente que sale por B y la que sale por C son diferentes, ya que están conectados de distinta forma a A. Según hemos dicho, desde A salen dos ramas en paralelo: una con resistencia R y una con resistencia R2. La corriente se reparte entre ambas en la forma

y

A su vez, esta corriente se divide en dos iguales, una por cada rama en paralelo.
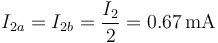
La corriente que sale por B es una de estas dos mitades
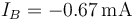
mientras que por C sale la otra mitad más la que va directamente desde A a C
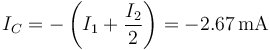
6 Solución general
6.1 Empleando la 1ª let de Kirchhoff y la ley de Ohm
Para el caso de que los tres voltajes, pero también para los caso anteriores, es más interesante hallar una solución general. Tenemos cinco resistencias y por cada una circulará una cierta corriente, cumpliéndose en cada una la ley de Ohm.
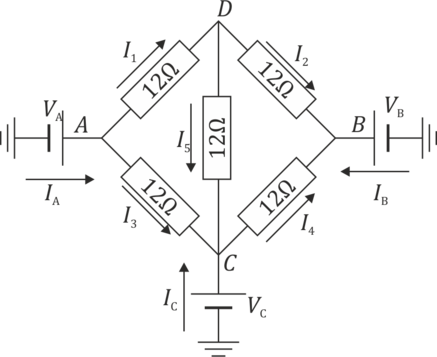
Según el esquema de la figura, aplicando aquí la 1ª ley de Kirchhoff para cada uno de los cuatro nodos queda

siendo IA la intensidad que entra por A, y análogamente para IB e IC. Por D no entra corriente.
El criterio es que se suman todas las corrientes que llegan a un nodo, precediéndolas de un signo - si salen de él. Esto no presupone que el resultado de cada una de estas intensidades vaya a ser un número positivo. Por ejemplo, necesariamente en B alguna de las tres intensidades debe resultar negativa.
Cada una de estas intensidades se relaciona con la diferencia de potencial entre sus extremos mediante la ley de Ohm:
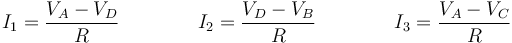

Con este sistema ya es suficiente para analizar cada caso, pero podemos dar una solución general para IA, IB e IC en función de VA, VB y VC.
Sustituimos la ley de Ohm en la ley de Kirchhoff para el nodo D y obtenemos el voltaje de este nodo

y llevamos este resultado al resto de nodos. Sustituimos en la ecuación para el nodo A
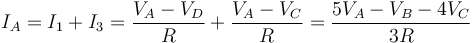
Sustituimos en la del nodo B
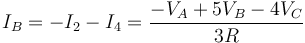
y en la del C
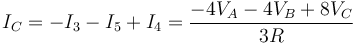
Este resultado se puede escribir en la forma matricial
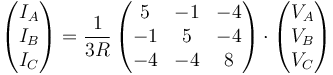
6.2 Empleando las dos leyes de Kirchhoff
Alternativamente, podemos llegar a estas ecuaciones aplicando la dos leyes de Kirchhoff. En ese caso debemos incluir las fuentes como parte del sistema, resultando un conjunto de cuatro mallas:

La ley de Kirchhoff de los nodos ya la hemos expuesto

y para las mallas resultan las cuatro ecuaciones

De la 3ª y la 4ª es inmediato que

Con las otras dos y con la 1ª ley para el nodo D llegamos a que
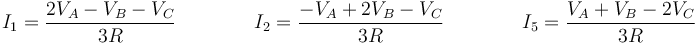
y con las leyes de Kirchhoff para los nodos A, B y C reobtenemos la solución matricial ya conocida.
Veamos de nuevo cada uno de los casos que hemos resuelto ya
6.3 Primer caso
En la primera situación tenemos

No conocemos IA, IB y VC. Esto nos da el sistema de ecuaciones
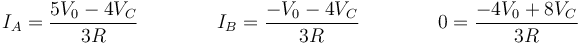
De la última resulta

y sustituyendo en las otras dos
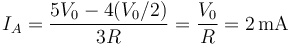
y
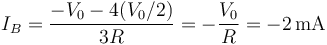
6.4 Segundo caso
En la segunda situación tenemos
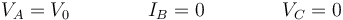
No conocemos IA, VB e IC. Esto nos da el sistema de ecuaciones
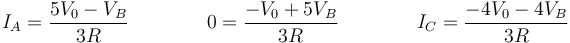
De la segunda resulta
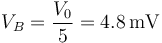
y sustituyendo en las otras dos

y
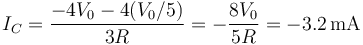
6.5 Tercer caso
El tercer caso es ahora más sencillo que los dos anteriores, ya que nos dan los tres voltajes
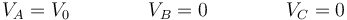
con lo que basta con sustituir
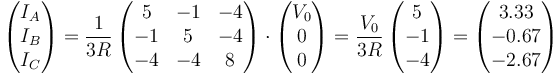
7 Cuarto caso
Una vez que tenemos la solución general, es inmediata su aplicación al cuarto caso
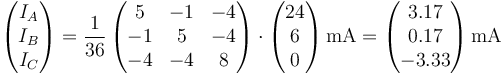
8 Quinto caso
De la misma manera se aplica al 5º
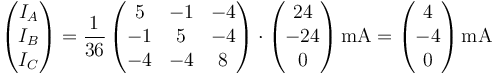
En este caso no entra ni sale corriente por el nodo C porque es análogo al primero de los casos que consideramos, con el nodo C en el voltaje medio entre A y B.
9 Sexto caso
Por último tenemos






