Potencial de esfera con hueco (GIOI)
De Laplace
(Página creada con '==Enunciado== {{nivel|3}} Para la esfera horadada del problema 1.19, calcule la diferencia de potencial entre los dos puntos diametralmente opuestos de la superficie exterior si…') |
(→Enunciado) |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | {{nivel|3}} Para la esfera horadada del problema | + | {{nivel|3}} Para la esfera horadada del problema “[[Campo_de_una_esfera_con_hueco_(GIOI)|Campo de una esfera con hueco]]”, calcule la diferencia de potencial entre los dos puntos diametralmente opuestos de la superficie exterior situados en la recta que pasa por los dos centros. |
| + | |||
| + | ==Solución== | ||
| + | Para el potencial también puede aplicarse el principio de superposición, como para el campo, con lo que la esfera hueca la vemos como suma de dos esferas macizas. | ||
| + | |||
| + | El potencial en el exterior de una esfera maciza uniformemente cargada equivale al de una carga puntual situada en su centro | ||
| + | |||
| + | <center><math>V=\frac{1}{4\pi\varepsilon_0}\,\frac{Q}{d}</math></center> | ||
| + | |||
| + | En este caso, que tenemos dos esferas, el potencial total será | ||
| + | |||
| + | <center><math>V=\frac{1}{4\pi\varepsilon_0}\,\left(\frac{Q_1}{d_1}+\frac{Q_2}{d_2}\right)</math></center> | ||
| + | |||
| + | El punto A se encuentra a una distancia de 10 cm del centro de la esfera grande y a 5 cm de la pequeña. El potencial en este punto vale | ||
| + | |||
| + | <center><math>V_A = 9\times 10^9\left(\frac{16\times 10^{-9}}{0.10}+\frac{-2\times 10^{-9}}{0.05}\right)\,\mathrm{V}=1080\,\mathrm{V}</math></center> | ||
| + | |||
| + | mientras que el punto B se encuentra también a 10 cm del centro la grande pero a 15 cm del centro de la pequeña, siendo su potencial | ||
| + | |||
| + | <center><math>V_B = 9\times 10^9\left(\frac{16\times 10^{-9}}{0.10}+\frac{-2\times 10^{-9}}{0.15}\right)\,\mathrm{V}=1320\,\mathrm{V}</math></center> | ||
| + | |||
| + | La diferencia de potencial entre los dos puntos vale | ||
| + | |||
| + | <center><math>\Delta V = V_B - V_A = 240\,\mathrm{V}</math></center> | ||
| + | |||
| + | Podemos observar que, puesto que A y B se encuentran a la misma distancia del centro de la esfera grande, lo único que cuenta para la d.d.p. es la distancia al centro de la esfera pequeña. | ||
| + | |||
| + | [[Categoría:Problemas de electrostática en el vacío (GIOI)]] | ||
última version al 13:32 8 mar 2020
1 Enunciado
![]() Para la esfera horadada del problema “Campo de una esfera con hueco”, calcule la diferencia de potencial entre los dos puntos diametralmente opuestos de la superficie exterior situados en la recta que pasa por los dos centros.
Para la esfera horadada del problema “Campo de una esfera con hueco”, calcule la diferencia de potencial entre los dos puntos diametralmente opuestos de la superficie exterior situados en la recta que pasa por los dos centros.
2 Solución
Para el potencial también puede aplicarse el principio de superposición, como para el campo, con lo que la esfera hueca la vemos como suma de dos esferas macizas.
El potencial en el exterior de una esfera maciza uniformemente cargada equivale al de una carga puntual situada en su centro
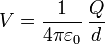
En este caso, que tenemos dos esferas, el potencial total será

El punto A se encuentra a una distancia de 10 cm del centro de la esfera grande y a 5 cm de la pequeña. El potencial en este punto vale
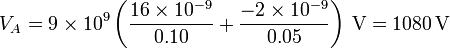
mientras que el punto B se encuentra también a 10 cm del centro la grande pero a 15 cm del centro de la pequeña, siendo su potencial
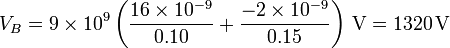
La diferencia de potencial entre los dos puntos vale
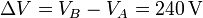
Podemos observar que, puesto que A y B se encuentran a la misma distancia del centro de la esfera grande, lo único que cuenta para la d.d.p. es la distancia al centro de la esfera pequeña.





