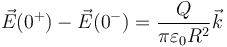Campo de un disco homogéneo (GIOI)
De Laplace
(Página creada con '==Solución== Una vez que tenemos el campo de un anillo podemos hallar el de un disco considerándolo como compuesto de anillos concéntricos. Cada uno de estos anillos tiene un…') |
(→Solución) |
||
| Línea 1: | Línea 1: | ||
| + | ==Enunciado== | ||
| + | {{nivel|3}} A partir del resultado del problema “[[Campo de un anillo homogéneo (GIOI)|Campo de un anillo homogéneo]]” calcule el campo en los puntos del eje de un disco circular de radio ''R'', en el cual existe una carga ''Q'' distribuida uniformemente. | ||
| + | |||
==Solución== | ==Solución== | ||
| - | Una vez que tenemos el campo de un anillo podemos hallar el de un disco considerándolo como compuesto de anillos concéntricos. Cada uno de estos anillos tiene una carga | + | Una vez que tenemos el [[Campo_de_un_anillo_homogéneo_(GIOI)|campo de un anillo]] |
| + | |||
| + | <center><math>\vec{E}(z\vec{k})=\frac{Qz}{4\pi\varepsilon_0(R^2+z^2)^{3/2}}\vec{k}</math></center> | ||
| + | |||
| + | podemos hallar el de un disco considerándolo como compuesto de anillos concéntricos. Cada uno de estos anillos tiene una carga | ||
<center><math>\mathrm{d}q = \sigma_s\,\mathrm{d}S = \frac{Q}{\pi R^2}(2\pi r')\,\mathrm{d}r'=\frac{2Q}{R^2}r'\,\mathrm{d}r'</math></center> | <center><math>\mathrm{d}q = \sigma_s\,\mathrm{d}S = \frac{Q}{\pi R^2}(2\pi r')\,\mathrm{d}r'=\frac{2Q}{R^2}r'\,\mathrm{d}r'</math></center> | ||
última version al 13:42 14 feb 2020
1 Enunciado
A partir del resultado del problema “Campo de un anillo homogéneo” calcule el campo en los puntos del eje de un disco circular de radio R, en el cual existe una carga Q distribuida uniformemente.
2 Solución
Una vez que tenemos el campo de un anillo
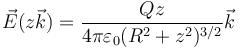
podemos hallar el de un disco considerándolo como compuesto de anillos concéntricos. Cada uno de estos anillos tiene una carga
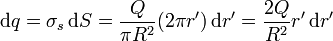
siendo r' el radio de cada anillo y dr' su espesor.
El campo que produce cada uno de estos anillos es, según el apartado anterior
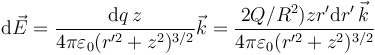
El campo total será la suma del de todos los anillos, cuyo radio varía desde 0 hasta R, el radio del disco
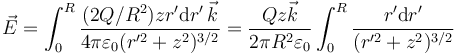
Esta integral se resuelve con el cambio de variable u = r'2 + z2 y el resultado es
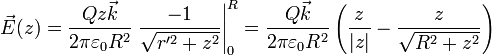
A la hora de sustituir los límites de integración hay que tener cuidado con los signos, ya que la raíz cuadrada es siempre positiva (máxime, tratándose de una distancia), por lo que
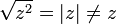
Este campo es, como en el caso del anillo, en la dirección del eje, con sentido hacia afuera (positivo para z > 0 y negativo para z < 0), pero no se anula en el centro. En el caso del anillo tenemos que se produce una discontinuidad de salto. Tenemos que
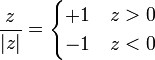
por lo que si nos acercamos a z=0 por encima del disco obtenemos el campo
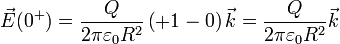
y por debajo de él
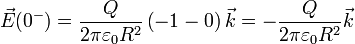
Tiene la misma magnitud en los dos límites, pero sentido opuesto. El salto en el campo vale
