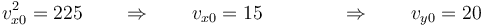Entrar Página Discusión Historial Go to the site toolbox

Tiro parabólico sobre árbol

De Laplace

(Diferencias entre revisiones)
 
(Una edición intermedia no se muestra.)
Línea 1: Línea 1:
==Enunciado==
==Enunciado==
Con un cañón se desea lanzar un proyectil que alcance a un blanco situado a una distancia horizontal <math>D=60\,\mathrm{m}</math>. La bala del cañón se mueve sometida a la acción de la gravedad (tómese <math>g=10\,\mathrm{m}/\mathrm{s}^2</math>). Entre el cañón y el blanco hay una hilera de cipreses de altura <math>h=15\,\mathrm{m}</math>, situado a una distancia <math>b=45\,\mathrm{m}</math> del cañón.
Con un cañón se desea lanzar un proyectil que alcance a un blanco situado a una distancia horizontal <math>D=60\,\mathrm{m}</math>. La bala del cañón se mueve sometida a la acción de la gravedad (tómese <math>g=10\,\mathrm{m}/\mathrm{s}^2</math>). Entre el cañón y el blanco hay una hilera de cipreses de altura <math>h=15\,\mathrm{m}</math>, situado a una distancia <math>b=45\,\mathrm{m}</math> del cañón.
-
<center>[[Archivo:parabolico-arboles-01.png]]</center>
+
<center>[[Archivo:parabolico-arboles-01.png|800px]]</center>
# Calcule la velocidad inicial <math>\vec{v}_0=v_x0 \vec{\imath}+v_y0 \vec{\jmath}</math> con la que debe lanzarse el proyectil si se quiere que impacte en el blanco y que la rapidez inicial sea mínima. ¿Cuánto valen la rapidez inicial y el ángulo de disparo?
# Calcule la velocidad inicial <math>\vec{v}_0=v_x0 \vec{\imath}+v_y0 \vec{\jmath}</math> con la que debe lanzarse el proyectil si se quiere que impacte en el blanco y que la rapidez inicial sea mínima. ¿Cuánto valen la rapidez inicial y el ángulo de disparo?
# Para la velocidad inicial anterior, halle la altura máxima que alcanza el proyectil.
# Para la velocidad inicial anterior, halle la altura máxima que alcanza el proyectil.
Línea 77: Línea 77:
<center><math>v_{x0}^2 = 225\qquad\Rightarrow \qquad v_{x0}=15\qquad\qquad \Rightarrow\qquad v_{y0}=20</math></center>
<center><math>v_{x0}^2 = 225\qquad\Rightarrow \qquad v_{x0}=15\qquad\qquad \Rightarrow\qquad v_{y0}=20</math></center>
-
<center>[[Archivo:parabolico-arboles-02.png]]</center>
+
<center>[[Archivo:parabolico-arboles-02.png|800px]]</center>

última version al 21:55 9 nov 2019

Contenido

1 Enunciado

Con un cañón se desea lanzar un proyectil que alcance a un blanco situado a una distancia horizontal 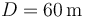D=60\,\mathrm{m}. La bala del cañón se mueve sometida a la acción de la gravedad (tómese 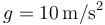g=10\,\mathrm{m}/\mathrm{s}^2). Entre el cañón y el blanco hay una hilera de cipreses de altura 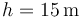h=15\,\mathrm{m}, situado a una distancia b=45\,\mathrm{m} del cañón.

  1. Calcule la velocidad inicial 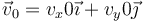\vec{v}_0=v_x0 \vec{\imath}+v_y0 \vec{\jmath} con la que debe lanzarse el proyectil si se quiere que impacte en el blanco y que la rapidez inicial sea mínima. ¿Cuánto valen la rapidez inicial y el ángulo de disparo?
  2. Para la velocidad inicial anterior, halle la altura máxima que alcanza el proyectil.
  3. Para el punto de altura máxima anterior, calcule la posición del centro de curvatura de la trayectoria.
  4. Si, una vez fijado el ángulo de tiro, el cañón tiene una incertidumbre de un 1% en la rapidez inicial, ¿cuál es la incertidumbre en la distancia de alcance?

2 Velocidad de disparo

\textbf{Todo lo que sigue en las unidades fundamentales del SI: distancias en m, tiempos en s}

En ausencia de rozamiento, el movimiento de un proyectil es un movimiento con aceleración constante. Separando por componentes y tomando como origen de coordenadas el punto de disparo:

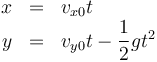
\begin{array}{rcl} x&=&v_{x0} t\\ y&=&v_{y0} t -\dfrac{1}{2}gt^2 \end{array}

Como debe impactar en el blanco en algún instante T

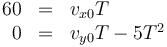
\begin{array}{rcl} 60 &=&v_{x0} T\\ 0&=&v_{y0} T -5T^2 \end{array}

Despejando T y sustituyendo llegamos a la relación

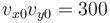
v_{x0}v_{y0}=300\,

Si escribimos

v_{x0}=v_0 \cos(\alpha)\qquad\qquad v_{y0}=v_0\,\mathrm{sen}(\alpha)

esta relación se convierte en

v_0^2 \mathrm{sen}(2\alpha)=600\qquad\Rightarrow \qquad v_0=\sqrt{\frac{600}{\mathrm{sen}(2\alpha)}}

2.1 Solución incorrecta

Para que sea mínima la velocidad, el valor del seno debe ser máximo, lo cual nos diría que el valor mínimo se alcanza para

2\alpha=90^\circ \qquad\Rightarrow \qquad \alpha=45^\circ\qquad\Rightarrow \qquad v_0=\sqrt{600}=10\sqrt{6}

siendo las componentes de la velocidad inicial

v_{x0}=v_{y0}=\frac{10\sqrt{6}}{\sqrt{2}}=10\sqrt{3}

Sin embargo, este resultado no tiene en cuenta la presencia de los árboles. Si calculamos la altura a la que pasa cuando x = 45

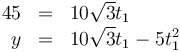
\begin{array}{rcl} 45 &=&10\sqrt{3} t_1\\ y&=&10\sqrt{3} t_1 -5t_1^2 \end{array}

lo que nos da

y=\frac{45}{4}=11.25

que al ser inferior a 15m implica que el proyectil impacta con el blanco.

2.2 Solución correcta

Puesto que la solución a 45° es demasiado baja, hay que ir elevando el proyectil hasta que pase por encima de los árboles. La solución mínima será aquella que pase rasante por la copa. Es decir, aquella que a x = 45 tenga y =15 m

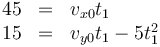
\begin{array}{rcl} 45 &=&v_{x0} t_1\\ 15 &=&v_{y0} t_1 -5t_1^2 \end{array}

Despejando el tiempo y sustituyendo queda

15 = \frac{45v_{y0}}{v_{x0}} - 5 \frac{45^2}{v_{x0}^2} \qquad\Rightarrow\qquad v_{x0}^2 = 3v_{x0}v_{y0}-675

Como antes teníamos que

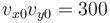
v_{x0}v_{y0}=300\,

Nos queda

v_{x0}^2 = 225\qquad\Rightarrow \qquad v_{x0}=15\qquad\qquad \Rightarrow\qquad v_{y0}=20
Obtenido de "http://tesla.us.es/wiki/index.php/Tiro_parab%C3%B3lico_sobre_%C3%A1rbol"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 21:55, 9 nov 2019. - Esta página ha sido visitada 617 veces. - Aviso legal - Acerca de Laplace