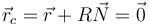Entrar Página Discusión Historial Go to the site toolbox

Movimiento circular en el plano OXY

De Laplace

(Diferencias entre revisiones)
(Página creada con '==Enunciado== Una partícula se mueve según la ecuación horaria <center><math>\vec{r}=A \cos⁡(\omega{}t) \vec{\imath}+A\,\mathrm{sen⁡}(\omega{}t)\vec{\jmath}</math></cente…')
(→Velocidad y rapidez)
 
(Una edición intermedia no se muestra.)
Línea 9: Línea 9:
##El triedro de Frenet <math>\{\vec{T},\vec{N},\vec{B}\}</math>
##El triedro de Frenet <math>\{\vec{T},\vec{N},\vec{B}\}</math>
##El radio y el centro de curvatura
##El radio y el centro de curvatura
 +
==Trayectoria==
 +
Circunferencia en el plano OXY y centrada en el origen.
 +
 +
Cumple
 +
 +
<center><math>x^2+y^2=A^2 \qquad\qquad z=0</math></center>
 +
==Velocidad y rapidez==
 +
===Velocidad===
 +
 +
<center><math>\vec{v}=-A\omega\,\mathrm{sen}(\omega t)\vec{\imath}+A\omega\cos(\omega t)\vec{\jmath}</math></center>
 +
 +
===Rapidez===
 +
 +
<center><math>\left|\vec{v}\right|=A\omega</math></center>
 +
 +
==Aceleración==
 +
 +
<center><math>\vec{a}=-A\omega^2 \cos⁡(\omega{}t) \vec{\imath}-A\omega^2\,\mathrm{sen⁡}(\omega{}t)\vec{\jmath}</math></center>
 +
 +
==Componentes intrínsecas==
 +
===Aceleración tangencial===
 +
 +
<center><math>a_t=0\qquad\qquad \vec{a}_t=\vec{0}</math></center>
 +
 +
==Aceleración normal===
 +
 +
<center><math>\vec{a}_n=\vec{a}=-A\omega^2 \cos⁡(\omega{}t)\vec{\imath}-A\omega^2\,\mathrm{sen⁡}(\omega{}t)\vec{\jmath}\qquad\qquad a_n=\left|\vec{a}_n\right|=A\omega^2</math></center>
 +
 +
==Triedro de Frenet==
 +
===Vector tangente===
 +
<center><math>\vec{T}=\frac{\vec{v}}{|\vec{v}|}=-\mathrm{sen}(\omega t)\vec{\imath}+\cos(\omega t)\vec{\jmath}</math></center>
 +
 +
===Vector normal===
 +
<center><math>\vec{N}=\frac{\vec{a}_n}{|\vec{a}_n|}=-\cos⁡(\omega{}t) \vec{\imath}-\mathrm{sen⁡}(\omega{}t)\vec{\jmath}</math></center>
 +
 +
===Vector binormal===
 +
<center><math>\vec{B}=\vec{T}\times\vec{N}=\vec{k}</math></center>
 +
 +
==Radio y centro de curvatura==
 +
===Radio de curvatura===
 +
 +
<center><math>R=\frac{|\vec{v}|^2}{|\vec{a}_n|}=A</math></center>
 +
 +
===Centro de curvatura===
 +
<center><math>\vec{r}_c=\vec{r}+R\vec{N}=\vec{0}</math></center>

última version al 12:20 19 oct 2019

Contenido

1 Enunciado

Una partícula se mueve según la ecuación horaria

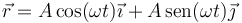
\vec{r}=A \cos⁡(\omega{}t) \vec{\imath}+A\,\mathrm{sen⁡}(\omega{}t)\vec{\jmath}
  1. Determine la trayectoria que sigue la partícula.
  2. Para cada instante t, halle:
    1. La velocidad y la rapidez.
    2. La aceleración.
    3. Las componentes intrínsecas de la aceleración, tanto en forma vectorial como escalar.
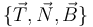
    4. El triedro de Frenet \{\vec{T},\vec{N},\vec{B}\}
    5. El radio y el centro de curvatura

2 Trayectoria

Circunferencia en el plano OXY y centrada en el origen.

Cumple

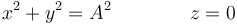
x^2+y^2=A^2 \qquad\qquad z=0

3 Velocidad y rapidez

3.1 Velocidad

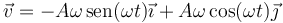
\vec{v}=-A\omega\,\mathrm{sen}(\omega t)\vec{\imath}+A\omega\cos(\omega t)\vec{\jmath}

3.2 Rapidez

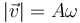
\left|\vec{v}\right|=A\omega

4 Aceleración

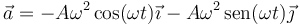
\vec{a}=-A\omega^2 \cos⁡(\omega{}t) \vec{\imath}-A\omega^2\,\mathrm{sen⁡}(\omega{}t)\vec{\jmath}

5 Componentes intrínsecas

5.1 Aceleración tangencial

a_t=0\qquad\qquad \vec{a}_t=\vec{0}

6 Aceleración normal=

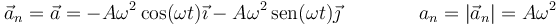
\vec{a}_n=\vec{a}=-A\omega^2 \cos⁡(\omega{}t)\vec{\imath}-A\omega^2\,\mathrm{sen⁡}(\omega{}t)\vec{\jmath}\qquad\qquad a_n=\left|\vec{a}_n\right|=A\omega^2

7 Triedro de Frenet

7.1 Vector tangente

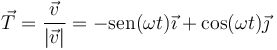
\vec{T}=\frac{\vec{v}}{|\vec{v}|}=-\mathrm{sen}(\omega t)\vec{\imath}+\cos(\omega t)\vec{\jmath}

7.2 Vector normal

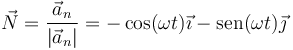
\vec{N}=\frac{\vec{a}_n}{|\vec{a}_n|}=-\cos⁡(\omega{}t) \vec{\imath}-\mathrm{sen⁡}(\omega{}t)\vec{\jmath}

7.3 Vector binormal

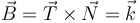
\vec{B}=\vec{T}\times\vec{N}=\vec{k}

8 Radio y centro de curvatura

8.1 Radio de curvatura

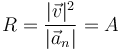
R=\frac{|\vec{v}|^2}{|\vec{a}_n|}=A

8.2 Centro de curvatura

\vec{r}_c=\vec{r}+R\vec{N}=\vec{0}
Obtenido de "http://tesla.us.es/wiki/index.php/Movimiento_circular_en_el_plano_OXY"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 12:20, 19 oct 2019. - Esta página ha sido visitada 1.366 veces. - Aviso legal - Acerca de Laplace