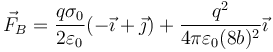Dos planos cargados ortogonales (GIE)
De Laplace
| (2 ediciones intermedias no se muestran.) | |||
| Línea 8: | Línea 8: | ||
<center>[[Archivo:dos-planos-ortogonales-01.png|400px]]</center> | <center>[[Archivo:dos-planos-ortogonales-01.png|400px]]</center> | ||
==Campo eléctrico== | ==Campo eléctrico== | ||
| - | El campo eléctrico debido a un plano cargado uniformemente vale | + | El campo eléctrico debido a un [[Campo_el%C3%A9ctrico_de_un_plano_y_de_dos_planos#Un_solo_plano|plano cargado uniformemente]] vale |
| - | <center><math>\vec{E}=\begin{cases}\dfrac{\sigma_0}{\varepsilon_0}\vec{k} & (z>0) \\ & \\ -\dfrac{\sigma_0}{\varepsilon_0}\vec{k} & (z<0) \end{cases}</math></center> | + | <center><math>\vec{E}=\begin{cases}\dfrac{\sigma_0}{2\varepsilon_0}\vec{k} & (z>0) \\ & \\ -\dfrac{\sigma_0}{2\varepsilon_0}\vec{k} & (z<0) \end{cases}</math></center> |
| - | siendo <math>\vec{k}</math> el vector perpendicular al plano, y z>0 o z < 0 se refiere a si estamos a un lado o al otro. El campo va a hacia afuera si la densidad de carga es positiva y hacia el plano si es negativa. Esta expresión se generaliza a cualquier otro plano. | + | siendo <math>\vec{k}</math> el vector perpendicular al plano, y z>0 o z < 0 se refiere a si estamos a un lado o al otro. |
| + | |||
| + | En cada semiespacio el campo es independiente de la posición. | ||
| + | |||
| + | El campo va a hacia afuera si la densidad de carga es positiva y hacia el plano si es negativa. Esta expresión se generaliza a cualquier otro plano. | ||
En nuestro caso tenemos dos planos de carga. El primero (“1”) sobre OXZ y el segundo (“2”) sobre OYZ. | En nuestro caso tenemos dos planos de carga. El primero (“1”) sobre OXZ y el segundo (“2”) sobre OYZ. | ||
| Línea 18: | Línea 22: | ||
El primero tiene por vector perpendicular a <math>\vec{\jmath}</math>, por lo que el campo que produce es | El primero tiene por vector perpendicular a <math>\vec{\jmath}</math>, por lo que el campo que produce es | ||
| - | <center><math>\vec{E}_1=\begin{cases}\dfrac{\sigma_0}{\varepsilon_0}\vec{\jmath} & (y>0) \\ & \\ -\dfrac{\sigma_0}{\varepsilon_0}\vec{\jmath} & (y<0) \end{cases}</math></center> | + | <center><math>\vec{E}_1=\begin{cases}\dfrac{\sigma_0}{2\varepsilon_0}\vec{\jmath} & (y>0) \\ & \\ -\dfrac{\sigma_0}{2\varepsilon_0}\vec{\jmath} & (y<0) \end{cases}</math></center> |
Para el segundo plano el vector <math>\vec{\imath}</math> y el campo que produce vale | Para el segundo plano el vector <math>\vec{\imath}</math> y el campo que produce vale | ||
| - | <center><math>\vec{E}_2=\begin{cases}\dfrac{\sigma_0}{\varepsilon_0}\vec{\imath} & (x>0) \\ & \\ -\dfrac{\sigma_0}{\varepsilon_0}\vec{\imath} & (x<0) \end{cases}</math></center> | + | <center><math>\vec{E}_2=\begin{cases}\dfrac{\sigma_0}{2\varepsilon_0}\vec{\imath} & (x>0) \\ & \\ -\dfrac{\sigma_0}{2\varepsilon_0}\vec{\imath} & (x<0) \end{cases}</math></center> |
Para el campo total sumamos estos dos. La suma hay que hacerla cuadrante a cuadrante. El resultado es | Para el campo total sumamos estos dos. La suma hay que hacerla cuadrante a cuadrante. El resultado es | ||
| - | <center><math>\vec{E}=\vec{E}_1+\vec{E}_2=\begin{cases}\dfrac{\sigma_0}{\varepsilon_0}(\vec{\imath}+\vec{\jmath}) & (x>0, y>0) \\ & \\ \dfrac{\sigma_0}{\varepsilon_0}(-\vec{\imath}+\vec{\jmath}) & (x<0, y>0) \\ & \\\dfrac{\sigma_0}{\varepsilon_0}(-\vec{\imath}-\vec{\jmath}) & (x<0, y<0) \\ & \\\dfrac{\sigma_0}{\varepsilon_0}(\vec{\imath}-\vec{\jmath}) & (x>0, y<0) \\ & \\\end{cases}</math></center> | + | <center><math>\vec{E}=\vec{E}_1+\vec{E}_2=\begin{cases}\dfrac{\sigma_0}{2\varepsilon_0}(\vec{\imath}+\vec{\jmath}) & (x>0, y>0) \\ & \\ \dfrac{\sigma_0}{2\varepsilon_0}(-\vec{\imath}+\vec{\jmath}) & (x<0, y>0) \\ & \\\dfrac{\sigma_0}{2\varepsilon_0}(-\vec{\imath}-\vec{\jmath}) & (x<0, y<0) \\ & \\\dfrac{\sigma_0}{2\varepsilon_0}(\vec{\imath}-\vec{\jmath}) & (x>0, y<0) \\ & \\\end{cases}</math></center> |
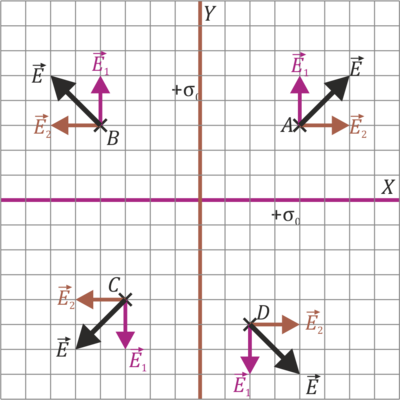
El campo es uniforme en cada cuadrante, formando en cada uno 45° con los ejes. | El campo es uniforme en cada cuadrante, formando en cada uno 45° con los ejes. | ||
| + | <center>[[Archivo:dos-planos-ortogonales-02.png|400px]]</center> | ||
==Líneas de campo== | ==Líneas de campo== | ||
Al ser constante el campo en cada cuadrante, las líneas de campo son rectas (semirrectas, para ser precisos) que parten de los planos y van al infinito formando en todo momento un ángulo de 45° con los ejes. | Al ser constante el campo en cada cuadrante, las líneas de campo son rectas (semirrectas, para ser precisos) que parten de los planos y van al infinito formando en todo momento un ángulo de 45° con los ejes. | ||
| + | |||
| + | <center>[[Archivo:dos-planos-ortogonales-03.png|400px]]</center> | ||
==Potencial eléctrico== | ==Potencial eléctrico== | ||
Las líneas equipotenciales son ortogonales al campo (y a las líneas de campo). Por tanto son líneas que forman también un ángulo de 45° con los ejes. Forman cuadrados con centro el origen. | Las líneas equipotenciales son ortogonales al campo (y a las líneas de campo). Por tanto son líneas que forman también un ángulo de 45° con los ejes. Forman cuadrados con centro el origen. | ||
| + | |||
| + | <center>[[Archivo:dos-planos-ortogonales-04.png|400px]]</center> | ||
| + | |||
==Trabajo== | ==Trabajo== | ||
| - | De las líneas equipotenciales del apartado anterior, hay una que pasa por los cuatro puntos. Por tanto, todos los puntos están al mismo potencial y el trabajo para ir de uno a otro es nulo. | + | De las líneas equipotenciales del apartado anterior, hay una que pasa por los cuatro puntos (marcada en un color diferente en la figura). Por tanto, todos los puntos están al mismo potencial y el trabajo para ir de uno a otro es nulo. |
| - | <center><math>W_{A\to B}=W_{A\to C}=W_{A\to D}=0\,</math></center> | + | <center><math>W_{A\to B}=q(V_B-V_A)=0\qquad\qquad W_{A\to C}=W_{A\to D}=0\,</math></center> |
==Fuerza sobre cargas== | ==Fuerza sobre cargas== | ||
La fuerza sobre la carga negativa es la suma de la que producen los planos más la que produce la carga negativa. Esta última la da la ley de Coulomb | La fuerza sobre la carga negativa es la suma de la que producen los planos más la que produce la carga negativa. Esta última la da la ley de Coulomb | ||
| - | <center><math>\vec{F}_A=-\frac{q\sigma_0}{\varepsilon_0}(\vec{\imath}+\vec{\jmath})-\frac{q^2}{4\pi\varepsilon_0(8b)^2}\vec{\imath}</math></center> | + | <center><math>\vec{F}_A=-\frac{q\sigma_0}{2\varepsilon_0}(\vec{\imath}+\vec{\jmath})-\frac{q^2}{4\pi\varepsilon_0(8b)^2}\vec{\imath}</math></center> |
y de manera análoga para la cara positiva | y de manera análoga para la cara positiva | ||
| - | <center><math>\vec{F}_B=\frac{q\sigma_0}{\varepsilon_0}(-\vec{\imath}+\vec{\jmath})+\frac{q^2}{4\pi\varepsilon_0(8b)^2}\vec{\imath}</math></center> | + | <center><math>\vec{F}_B=\frac{q\sigma_0}{2\varepsilon_0}(-\vec{\imath}+\vec{\jmath})+\frac{q^2}{4\pi\varepsilon_0(8b)^2}\vec{\imath}</math></center> |
última version al 22:55 12 sep 2018
Contenido |
1 Enunciado
Un sistema de cargas está formado por dos planos cargados, ambos con la misma densidad de carga + σ0, situados ortogonalmente. Uno de ellos coincide con el plano OXZ y el otro con el OYZ.
- Halle el campo eléctrico en los puntos A(4b,3b,0), B(−4b,3b,0), C(−3b,−4b,0) y D(2b,−5b,0). Puede usarse, si se conoce, la expresión del campo creado por un solo plano.
- Indique gráficamente cómo son las líneas de campo en cada uno de los cuatro cuadrantes.
- Indique gráficamente cómo son las superficies equipotenciales en este sistema
- Calcule el trabajo necesario para mover una carga q0 desde A hasta B; para mover la misma carga desde A a C, y para moverla desde A a D.
- Suponga que se sitúa una carga − q0 en el punto A y otra + q0 en la posición simétrica B ¿Cuánto vale la fuerza eléctrica sobre cada una de estas dos cargas?

2 Campo eléctrico
El campo eléctrico debido a un plano cargado uniformemente vale
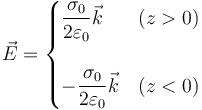
siendo  el vector perpendicular al plano, y z>0 o z < 0 se refiere a si estamos a un lado o al otro.
el vector perpendicular al plano, y z>0 o z < 0 se refiere a si estamos a un lado o al otro.
En cada semiespacio el campo es independiente de la posición.
El campo va a hacia afuera si la densidad de carga es positiva y hacia el plano si es negativa. Esta expresión se generaliza a cualquier otro plano.
En nuestro caso tenemos dos planos de carga. El primero (“1”) sobre OXZ y el segundo (“2”) sobre OYZ.
El primero tiene por vector perpendicular a  , por lo que el campo que produce es
, por lo que el campo que produce es
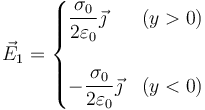
Para el segundo plano el vector  y el campo que produce vale
y el campo que produce vale
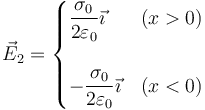
Para el campo total sumamos estos dos. La suma hay que hacerla cuadrante a cuadrante. El resultado es

El campo es uniforme en cada cuadrante, formando en cada uno 45° con los ejes.
3 Líneas de campo
Al ser constante el campo en cada cuadrante, las líneas de campo son rectas (semirrectas, para ser precisos) que parten de los planos y van al infinito formando en todo momento un ángulo de 45° con los ejes.

4 Potencial eléctrico
Las líneas equipotenciales son ortogonales al campo (y a las líneas de campo). Por tanto son líneas que forman también un ángulo de 45° con los ejes. Forman cuadrados con centro el origen.

5 Trabajo
De las líneas equipotenciales del apartado anterior, hay una que pasa por los cuatro puntos (marcada en un color diferente en la figura). Por tanto, todos los puntos están al mismo potencial y el trabajo para ir de uno a otro es nulo.

6 Fuerza sobre cargas
La fuerza sobre la carga negativa es la suma de la que producen los planos más la que produce la carga negativa. Esta última la da la ley de Coulomb

y de manera análoga para la cara positiva