Cilindro que cambia de baño térmico (GIE)
De Laplace
(Página creada con '==Enunciado== Se tiene un tubo hermético, de 16 cm² de sección, cerrado por un émbolo móvil. Las paredes y el émbolo están forrados con un aislante térmico imperfecto,…') |
|||
| (Una edición intermedia no se muestra.) | |||
| Línea 10: | Línea 10: | ||
# La variación de energía interna y de entalpía en cada paso | # La variación de energía interna y de entalpía en cada paso | ||
# La variación de entropía del gas y del ambiente en cada proceso. | # La variación de entropía del gas y del ambiente en cada proceso. | ||
| - | '''Dato:''' Constante universal de los gases ideales R=8.314 J | + | '''Dato:''' Constante universal de los gases ideales R=8.314 J/K·mol |
| + | ==Variables de estado== | ||
| + | En el estado inicial, como se indica, tenemos la presión, temperatura y volumen | ||
| + | |||
| + | <center><math>p_A=100\,\mathrm{kPa}\qquad\qquad T_A=300\,\mathrm{K}\qquad\qquad V_A=0.160\,\mathrm{L}</math></center> | ||
| + | |||
| + | El primer proceso, con el pistón libre, es una expansión a presión constante | ||
| + | |||
| + | <center><math>p_B=p_A=100\,\mathrm{kPa}</math></center> | ||
| + | |||
| + | El nuevo volumen es | ||
| + | |||
| + | <center><math>v_B=0.200\,\mathrm{L}</math></center> | ||
| + | |||
| + | y la temperatura, por la ley de Charles (o la de los gases ideales) | ||
| + | |||
| + | <center><math>\frac{100\times 0.200}{T_B}=\frac{100\times 0.160}{300}\qquad\Rightarrow\qquad T_B=375\,\mathrm{K}</math></center> | ||
| + | |||
| + | El segundo proceso, con el pistón fijado es a volumen constante | ||
| + | |||
| + | <center><math>V_C=V_B= 0.200\,\mathrm{L}</math></center> | ||
| + | |||
| + | La temperatura vuelve a ser la inicial | ||
| + | |||
| + | <center><math>T_C=T_A=300\,\mathrm{K}</math></center> | ||
| + | |||
| + | y la presión sale de la ley de los gases ideales | ||
| + | |||
| + | <center><math>\frac{p_C\times 0.200}{300}=\frac{100\times 0.200}{375}\qquad\Rightarrow\qquad p_C=80\,\mathrm{kPa}</math></center> | ||
| + | |||
| + | ==Trabajo, calor, energía y entalpía== | ||
| + | ===Primer paso=== | ||
| + | El primer paso es una expansión cuasiestática a presión constante. El trabajo realizado es | ||
| + | |||
| + | <center><math>W_{A\to B}=-p_A(V_B-V_A)=-100\,\mathrm{kPa}(0.200-0.160)\mathrm{L}=-4\,\mathrm{J}</math></center> | ||
| + | |||
| + | El aumento de energía interna vale | ||
| + | |||
| + | <center><math>\Delta U=nc_v(T_B-T_A)=\frac{p_BV_B-p_AV_A}{\gamma-1}=10\,\mathrm{J}</math></center> | ||
| + | |||
| + | y el de la entalpía | ||
| + | |||
| + | <center><math>\Delta H=nc_p(T_B-T_A)=\frac{\gamma (p_BV_B-p_AV_A)}{\gamma-1}=14\,\mathrm{J}</math></center> | ||
| + | |||
| + | En un proceso cuasiestático a presión constante, el calor es igual al aumento de entalpía | ||
| + | |||
| + | <center><math>Q_{A\to B}=\Delta H = 14\,\mathrm{J}</math></center> | ||
| + | |||
| + | También sale del primer principio | ||
| + | |||
| + | <center><math>Q_{A\to B} = \Delta U-W_{A\to B} = 10\,\mathrm{J}-(-4\,\mathrm{J})=14\,\mathrm{J}</math></center> | ||
| + | |||
| + | ===Segundo paso=== | ||
| + | El segundo paso es un enfriamiento a volumen constante. Por ello, el trabajo es nulo | ||
| + | |||
| + | <center><math>W_{B\to C}=0\,</math></center> | ||
| + | |||
| + | y la variación de energía interna es la opuesta a la de antes | ||
| + | |||
| + | <center><math>\Delta U=nc_v(T_C-T_B)=\frac{p_CV_C-p_BV_B}{\gamma-1}=-10\,\mathrm{J}</math></center> | ||
| + | |||
| + | y lo mismo ocurre con la entalpía | ||
| + | |||
| + | <center><math>\Delta H=nc_p(T_C-T_B)=\frac{\gamma (p_CV_C-p_BV_B)}{\gamma-1}=-14\,\mathrm{J}</math></center> | ||
| + | |||
| + | En un proceso a volumen constante, el calor coincide con la variación de la energía interna | ||
| + | |||
| + | <center><math>Q=\Delta U = -10\,\mathrm{J}</math></center> | ||
| + | |||
| + | ===Tercer paso=== | ||
| + | El tercer paso ''no'' es cuasiestático. La presión interior no permanece constante, ni el volumen, ni tampoco la temperatura (aunque la inicial sea igual a la final). | ||
| + | |||
| + | Sí es constante la presión exterior, por lo que el trabajo se puede calcular como | ||
| + | |||
| + | <center><math>W_{C\to A}=-p_\mathrm{ext}(V_A-V_C)= -100\,\mathrm{kPa}(0.160-0.200)=+3\,\mathrm{J}</math></center> | ||
| + | |||
| + | Como la temperatura es la misma al final que al principio del paso, la energía interna no cambia | ||
| + | |||
| + | <center><math>\Delta U = nc_v(T_A-T_C)=0\,</math></center> | ||
| + | |||
| + | y lo mismo ocurre con la entalpía | ||
| + | |||
| + | <center><math>\Delta H = nc_p(T_A-T_C)=0\,</math></center> | ||
| + | |||
| + | El calor sale del primer principio de la termodinámica | ||
| + | |||
| + | <center><math>Q_{C\to A} = \Delta U-W_{C\to A} = 0\,\mathrm{J}-4\,\mathrm{J}=-4\,\mathrm{J}</math></center> | ||
| + | |||
| + | ===Diagrama del ciclo=== | ||
| + | Los dos primeros pasos son cuasiestáticos y se representan, respectivamente, por un tramo horizontal y uno vertical. El tercero no es cuasiestático y por tanto no puede representarse. | ||
| + | ==Entropía== | ||
| + | En todos los pasos podemos calcular la variación de entropía del sistema como | ||
| + | |||
| + | <center><math>\Delta S_\mathrm{sis}=nc_p\ln\left(\frac{v_f}{V_i}\right)+nc_v\ln\left(\frac{p_f}{p_i}\right)=\frac{\gamma p_AV_A}{(\gamma-1)T_A}\ln\left(\frac{v_f}{V_i}\right)+\frac{ p_AV_A}{(\gamma-1)T_A}\ln\left(\frac{p_f}{p_i}\right)</math></center> | ||
| + | |||
| + | mientras que el ambiente es uno u otro baño térmico, para cada uno de los cuales se cumple | ||
| + | |||
| + | <center><math>\Delta S = \frac{Q_\mathrm{amb}}{T}</math></center> | ||
| + | |||
| + | con <math>Q_\mathrm{amb}</math> el calor que entra en el ambiente (esto es, el que sale del sistema; esto es, el que entra en el sistema cambiado de signo). | ||
| + | |||
| + | Esto da | ||
| + | ===Primer paso=== | ||
| + | Para el sistema | ||
| + | |||
| + | <center><math>\Delta S_\mathrm{sis} = \frac{1.4\times 100\times0.160}{1.4-1}\ln\left(\frac{0.200}{0.160}\right)=+41.7\,\frac{\mathrm{mJ}}{\mathrm{K}}</math></center> | ||
| + | |||
| + | para el ambiente | ||
| + | |||
| + | <center><math>\Delta S_\mathrm{amb} = \frac{-14\,\mathrm{J}}{375\,\mathrm{K}}=-37.3\frac{\mathrm{mJ}}{\mathrm{K}}</math></center> | ||
| + | |||
| + | y para el universo | ||
| + | |||
| + | <center><math>\Delta S_u=\Delta S_\mathrm{sis}+\Delta S_\mathrm{amb}=+4.32\frac{\mathrm{mJ}}{\mathrm{K}}</math></center> | ||
| + | |||
| + | ===Segundo paso=== | ||
| + | Para el sistema | ||
| + | |||
| + | <center><math>\Delta S_\mathrm{sis} = \frac{100\times 0.160}{1.4-1}\ln\left(\frac{80}{100}\right)=-29.8\,\frac{\mathrm{mJ}}{\mathrm{K}}</math></center> | ||
| + | |||
| + | para el ambiente | ||
| + | |||
| + | <center><math>\Delta S_\mathrm{amb} = \frac{+10\,\mathrm{J}}{300\,\mathrm{K}}=+33.3\frac{\mathrm{mJ}}{\mathrm{K}}</math></center> | ||
| + | |||
| + | y para el universo | ||
| + | |||
| + | <center><math>\Delta S_u=\Delta S_\mathrm{sis}+\Delta S_\mathrm{amb}=+3.58\frac{\mathrm{mJ}}{\mathrm{K}}</math></center> | ||
| + | |||
| + | ===Tercer paso=== | ||
| + | Para el sistema | ||
| + | |||
| + | <center><math>\Delta S_\mathrm{sis} = \frac{1.4\times 100\times0.160}{1.4-1}\ln\left(\frac{0.160}{0.200}\right)+\frac{100\times 0.160}{1.4-1}\ln\left(\frac{100}{80}\right)=-11.9\,\frac{\mathrm{mJ}}{\mathrm{K}}</math></center> | ||
| + | |||
| + | Es la suma de los dos anteriores cambiada de signo, como corresponde a un proceso cíclico. La variación total de entropía del sistema es nula. | ||
| + | |||
| + | Para el ambiente | ||
| + | |||
| + | <center><math>\Delta S_\mathrm{amb} = \frac{+4\,\mathrm{J}}{300\,\mathrm{K}}=+13.3\frac{\mathrm{mJ}}{\mathrm{K}}</math></center> | ||
| + | |||
| + | y para el universo | ||
| + | |||
| + | <center><math>\Delta S_u=\Delta S_\mathrm{sis}+\Delta S_\mathrm{amb}=+1.43\frac{\mathrm{mJ}}{\mathrm{K}}</math></center> | ||
| + | |||
| + | ===En el ciclo completo=== | ||
| + | Para el sistema | ||
| + | |||
| + | <center><math>\Delta S_\mathrm{sis}=\Delta S^{A\to B}_\mathrm{sis}+\Delta S^{B\to C}_\mathrm{sis}+\Delta S^{C\to A}_\mathrm{sis}=+41.7-29.8-11.9=0\,\frac{\mathrm{mJ}}{\mathrm{K}}</math></center> | ||
| + | |||
| + | Para el ambiente | ||
| + | |||
| + | <center><math>\Delta S_\mathrm{amb}=\Delta S^{A\to B}_\mathrm{amb}+\Delta S^{B\to C}_\mathrm{amb}+\Delta S^{C\to A}_\mathrm{amb}=-37.3+33.3-13.3=+9.33\,\frac{\mathrm{mJ}}{\mathrm{K}}</math></center> | ||
| + | |||
| + | y para el universo | ||
| + | |||
| + | <center><math>\Delta S_u=\Delta S_\mathrm{sis}+\Delta S_\mathrm{amb}=+9.33\,\frac{\mathrm{mJ}}{\mathrm{K}}</math></center> | ||
| + | |||
| + | Vemos que, por tratarse de un ciclo irreversible, al final del ciclo la entropía del sistema no ha cambiado, pero la del ambiente (y por tanto la del universo) ha aumentado. | ||
última version al 00:11 12 sep 2018
Contenido |
1 Enunciado
Se tiene un tubo hermético, de 16 cm² de sección, cerrado por un émbolo móvil. Las paredes y el émbolo están forrados con un aislante térmico imperfecto, que permite el calentamiento o enfriamiento gradual del interior. En el interior del tubo hay aire seco (γ=1.4). El tubo se halla en posición vertical, con el émbolo en su parte superior. Inicialmente el émbolo se encuentra a 10.0 cm de la base, estando el aire interior a 100kPa y 300K, que también es la presión exterior y la temperatura del baño térmico en que está sumergido.
- Se lleva el cilindro a un baño térmico de mayor temperatura y la misma presión, provocando que suba el pistón pasando, cuando se alcanza el nuevo equilibrio térmico, a estar a una altura de 12.5 cm respecto al fondo.
- En esa posición se colocan topes en el pistón, inmovilizándolo. Se procede entonces a llevar de nuevo al émbolo al baño térmico inicial a 300K y se deja que alcance de nuevo el equilibrio térmico.
- En este estado, se libera bruscamente el émbolo, que retorna rápidamente a su posición inicial
Halle
- La presión, temperatura y volumen del gas interior al final de cada paso. Represente esquemáticamente el ciclo en un diagrama pV.
- El trabajo realizado sobre el gas en cada paso, así como el calor que entra o sale del gas en cada paso.
- La variación de energía interna y de entalpía en cada paso
- La variación de entropía del gas y del ambiente en cada proceso.
Dato: Constante universal de los gases ideales R=8.314 J/K·mol
2 Variables de estado
En el estado inicial, como se indica, tenemos la presión, temperatura y volumen

El primer proceso, con el pistón libre, es una expansión a presión constante
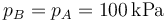
El nuevo volumen es

y la temperatura, por la ley de Charles (o la de los gases ideales)

El segundo proceso, con el pistón fijado es a volumen constante

La temperatura vuelve a ser la inicial
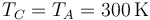
y la presión sale de la ley de los gases ideales
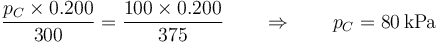
3 Trabajo, calor, energía y entalpía
3.1 Primer paso
El primer paso es una expansión cuasiestática a presión constante. El trabajo realizado es

El aumento de energía interna vale

y el de la entalpía
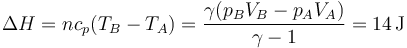
En un proceso cuasiestático a presión constante, el calor es igual al aumento de entalpía
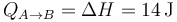
También sale del primer principio

3.2 Segundo paso
El segundo paso es un enfriamiento a volumen constante. Por ello, el trabajo es nulo
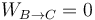
y la variación de energía interna es la opuesta a la de antes
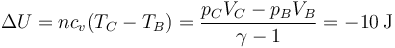
y lo mismo ocurre con la entalpía

En un proceso a volumen constante, el calor coincide con la variación de la energía interna

3.3 Tercer paso
El tercer paso no es cuasiestático. La presión interior no permanece constante, ni el volumen, ni tampoco la temperatura (aunque la inicial sea igual a la final).
Sí es constante la presión exterior, por lo que el trabajo se puede calcular como
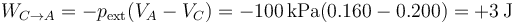
Como la temperatura es la misma al final que al principio del paso, la energía interna no cambia

y lo mismo ocurre con la entalpía

El calor sale del primer principio de la termodinámica

3.4 Diagrama del ciclo
Los dos primeros pasos son cuasiestáticos y se representan, respectivamente, por un tramo horizontal y uno vertical. El tercero no es cuasiestático y por tanto no puede representarse.
4 Entropía
En todos los pasos podemos calcular la variación de entropía del sistema como

mientras que el ambiente es uno u otro baño térmico, para cada uno de los cuales se cumple

con Qamb el calor que entra en el ambiente (esto es, el que sale del sistema; esto es, el que entra en el sistema cambiado de signo).
Esto da
4.1 Primer paso
Para el sistema

para el ambiente
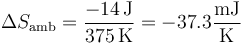
y para el universo

4.2 Segundo paso
Para el sistema

para el ambiente

y para el universo
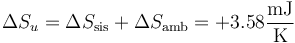
4.3 Tercer paso
Para el sistema

Es la suma de los dos anteriores cambiada de signo, como corresponde a un proceso cíclico. La variación total de entropía del sistema es nula.
Para el ambiente
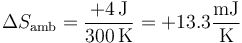
y para el universo

4.4 En el ciclo completo
Para el sistema

Para el ambiente
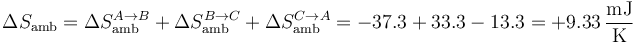
y para el universo
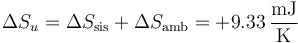
Vemos que, por tratarse de un ciclo irreversible, al final del ciclo la entropía del sistema no ha cambiado, pero la del ambiente (y por tanto la del universo) ha aumentado.





