Entrar Página Discusión Historial Go to the site toolbox

Movimiento con velocidad en dos instantes (GIE)

De Laplace

(Diferencias entre revisiones)
 
Línea 8: Línea 8:
## El radio y el centro de curvatura del movimiento.
## El radio y el centro de curvatura del movimiento.
==Aceleración==
==Aceleración==
 +
En lo que sigue, todas las posiciones están en m, tiempos en s, velocidades en m/s y aceleraciones en m/s².
 +
Por ser de aceleración constante
Por ser de aceleración constante
Línea 14: Línea 16:
Sustituyendo <math>t=2\,\mathrm{s}</math>
Sustituyendo <math>t=2\,\mathrm{s}</math>
-
<center><math>\vec{a}=\frac{\vec{v}_2-\vec{v}_0}{2}=\frac{\left(-0.80\vec{\imath}-0.80\vec{\jmath}+3.20\vec{k}\right)-\left(0.20\vec{\imath}-0.40\vec{\jmath}+0.40\vec{k}\right)}{2}=\left(-0.50\vec{\imath}-0.20\vec{\jmath}+1.40\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
+
<center><math>\vec{a}=\frac{\vec{v}_2-\vec{v}_0}{2}=\frac{\left(-0.80\vec{\imath}-0.80\vec{\jmath}+3.20\vec{k}\right)\mathrm{m}/\mathrm{s}-\left(0.20\vec{\imath}-0.40\vec{\jmath}+0.40\vec{k}\right)\mathrm{m}/\mathrm{s}}{2\,\mathrm{s}}=\left(-0.50\vec{\imath}-0.20\vec{\jmath}+1.40\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}^2}</math></center>
==Posición en t = 2&thinsp;s==
==Posición en t = 2&thinsp;s==
Por ser de aceleración constante
Por ser de aceleración constante

última version al 10:13 8 sep 2018

Contenido

1 Enunciado

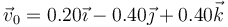Una partícula describe un movimiento con aceleración constante, tal que en t=0\,\mathrm{s} se halla en el origen de coordenadas moviéndose con velocidad \vec{v}_0=0.20\vec{\imath}-0.40\vec{\jmath}+0.40\vec{k} (m/s). En t=2\,\mathrm{s} su velocidad es 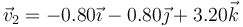\vec{v}_2=-0.80\vec{\imath}-0.80\vec{\jmath}+3.20\vec{k} (m/s). Halle

  1. La aceleración de la partícula.
  2. La posición de la partícula en t=2\,\mathrm{s}
  3. Para el instante t=0\,\mathrm{s}, calcule
    1. Las componentes intrínsecas de la aceleración (escalares y vectoriales).
    2. Los tres vectores del triedro de Frenet.
    3. El radio y el centro de curvatura del movimiento.

2 Aceleración

En lo que sigue, todas las posiciones están en m, tiempos en s, velocidades en m/s y aceleraciones en m/s².

Por ser de aceleración constante

\vec{v}(t)=\vec{v}_0+\vec{a}t

Sustituyendo t=2\,\mathrm{s}

\vec{a}=\frac{\vec{v}_2-\vec{v}_0}{2}=\frac{\left(-0.80\vec{\imath}-0.80\vec{\jmath}+3.20\vec{k}\right)\mathrm{m}/\mathrm{s}-\left(0.20\vec{\imath}-0.40\vec{\jmath}+0.40\vec{k}\right)\mathrm{m}/\mathrm{s}}{2\,\mathrm{s}}=\left(-0.50\vec{\imath}-0.20\vec{\jmath}+1.40\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}^2}

3 Posición en t = 2 s

Por ser de aceleración constante

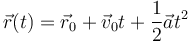
\vec{r}(t)=\vec{r}_0+\vec{v}_0t+\frac{1}{2}\vec{a}t^2

Sustituyendo t=2\,\mathrm{s}

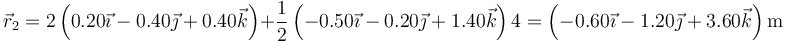
\vec{r}_2=2\left(0.20\vec{\imath}-0.40\vec{\jmath}+0.40\vec{k}\right)+\frac{1}{2}\left(-0.50\vec{\imath}-0.20\vec{\jmath}+1.40\vec{k}\right)·4=\left(-0.60\vec{\imath}-1.20\vec{\jmath}+3.60\vec{k}\right)\mathrm{m}

4 Magnitudes en t=2 s

4.1 Aceleración tangencial

El vector tangente es el unitario en la dirección y sentido de la velocidad

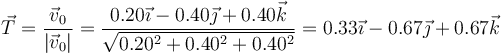
\vec{T}=\frac{\vec{v}_0}{|\vec{v}_0|}=\frac{0.20\vec{\imath}-0.40\vec{\jmath}+0.40\vec{k}}{\sqrt{0.20^2+0.40^2+0.40^2}}=0.33\vec{\imath}-0.67\vec{\jmath}+0.67\vec{k}

y la componente tangencial de la aceleración es

a_t=\vec{a}\cdot\vec{T}=0.90\,\frac{\mathrm{m}}{\mathrm{s}^2}

El vector aceleración tangencial vale

\vec{a}_t=a_t\vec{T}=\left(0.30\vec{\imath}-0.60\vec{\jmath}+0.60\vec{k}\right)\,\frac{\mathrm{m}}{\mathrm{s}^2}

4.2 Aceleración normal

Restamos de la aceleración completa

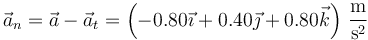
\vec{a}_n=\vec{a}-\vec{a}_t=\left(-0.80\vec{\imath}+0.40\vec{\jmath}+0.80\vec{k}\right)\,\frac{\mathrm{m}}{\mathrm{s}^2}

y en módulo

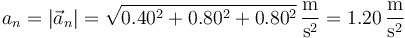
a_n=|\vec{a}_n|=\sqrt{0.40^2+0.80^2+0.80^2}\,\frac{\mathrm{m}}{\mathrm{s}^2}=1.20\,\frac{\mathrm{m}}{\mathrm{s}^2}

4.3 Triedro de Frenet

El vector tangente ya lo tenemos

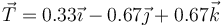
\vec{T}=0.33\vec{\imath}-0.67\vec{\jmath}+0.67\vec{k}

El normal es el unitario en la dirección y sentido de la aceleración normal

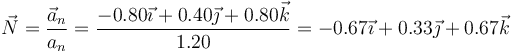
\vec{N}=\frac{\vec{a}_n}{a_n}=\frac{-0.80\vec{\imath}+0.40\vec{\jmath}+0.80\vec{k}}{1.20}=-0.67\vec{\imath}+0.33\vec{\jmath}+0.67\vec{k}

y el binormal es el producto de estos dos

\vec{B}=\left|\begin{matrix}\vec{\imath}&\vec{\jmath}&\vec{k}\\ 0.33 & -0.67 & 0.67 \\ -0.67 & 0.33 & 0.67\end{matrix}\right|=-0.67\vec{\imath}-0.67\vec{\jmath}-0.33\vec{k}

4.4 Radio y centro de curvatura

A partir de la aceleración normal

R=\frac{|\vec{v}|^2}{a_n}=\frac{0.60^2}{1.20}=0.30\,\mathrm{m}

siendo el centro de curvatura

\vec{r}_c=\vec{r}_0+R\vec{N}=\left(-0.20\vec{\imath}+0.10\vec{\jmath}+0.20\vec{k}\right)\mathrm{m}
Obtenido de "http://tesla.us.es/wiki/index.php/Movimiento_con_velocidad_en_dos_instantes_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 10:13, 8 sep 2018. - Esta página ha sido visitada 1.110 veces. - Aviso legal - Acerca de Laplace