Solución de onda estacionaria
De Laplace
(→Solución) |
|||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 3: | Línea 3: | ||
Una perturbación de una cuerda es de la forma | Una perturbación de una cuerda es de la forma | ||
| - | <center><math>y =0. | + | <center><math>y =0.200\cos(126t)\,\mathrm{sen}\,(0.314x)</math></center> |
con ''x'' e ''y'' medidos en centímetros y ''t'' en segundos. Demuestre que esta función verifica la ecuación de ondas. ¿Qué velocidad le | con ''x'' e ''y'' medidos en centímetros y ''t'' en segundos. Demuestre que esta función verifica la ecuación de ondas. ¿Qué velocidad le | ||
| Línea 9: | Línea 9: | ||
==Solución== | ==Solución== | ||
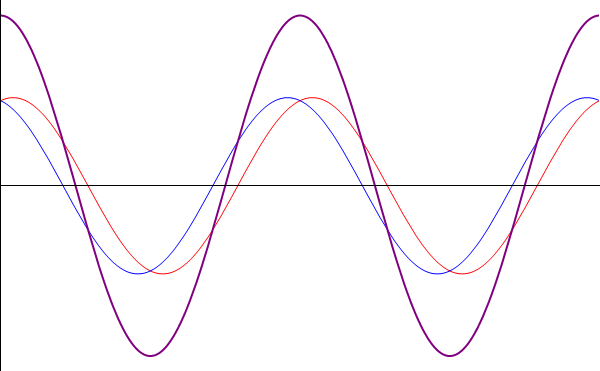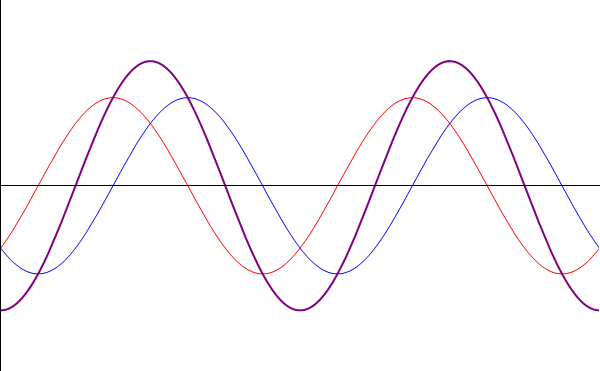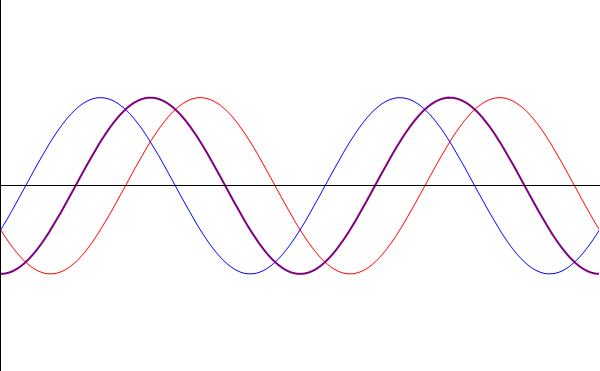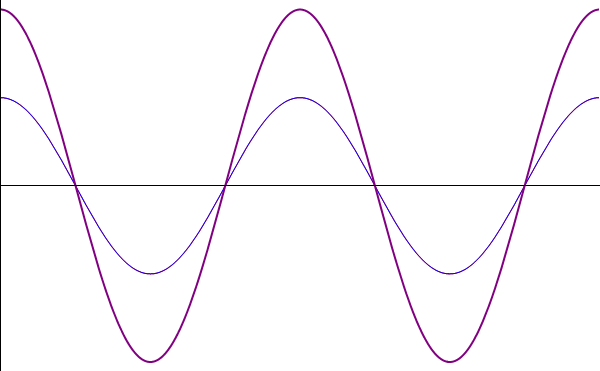
| - | [[Imagen:Estacio1.gif|left]] Hay que señalar que la forma de esta solución no es una señal que viaje ni hacia la derecha ni hacia la izquierda. | + | [[Imagen:Estacio1.gif|left]] Hay que señalar que la forma de esta solución no es una señal que viaje ni hacia la derecha ni hacia la izquierda. Es lo que se denomina una ''onda estacionaria''. |
Comenzamos escribiendo esta solución en la forma más general | Comenzamos escribiendo esta solución en la forma más general | ||
| - | <center><math>y =A\cos(\omega t)\,\mathrm{sen}\,(k x)</math>{{qquad}}<math>A=0. | + | <center><math>y =A\cos(\omega t)\,\mathrm{sen}\,(k x)</math>{{qquad}}<math>A=0.200\,\mathrm{cm}</math>{{qquad}}<math>\omega=126\,\mathrm{s}^{-1}</math>{{qquad}}<math>k=0.314\,\mathrm{cm}^{-1}</math></center> |
Se trata de demostrar que esta solución cumple una ecuación de la forma | Se trata de demostrar que esta solución cumple una ecuación de la forma | ||
| Línea 33: | Línea 33: | ||
<center><math>\frac{\partial^2 y}{\partial x^2}-\frac{1}{v^2}\,\frac{\partial^2 y}{\partial t^2} = -k^2y+\frac{\omega^2}{v^2}y=-\left(k^2-\frac{\omega^2}{v^2}\right)y</math></center> | <center><math>\frac{\partial^2 y}{\partial x^2}-\frac{1}{v^2}\,\frac{\partial^2 y}{\partial t^2} = -k^2y+\frac{\omega^2}{v^2}y=-\left(k^2-\frac{\omega^2}{v^2}\right)y</math></center> | ||
| - | Esta expresión se anula en todo instante y para todos los puntos si | + | Esta expresión se anula en todo instante y para todos los puntos si la velocidad de las ondas es |
<center><math>k^2-\frac{\omega^2}{v^2}</math>{{tose}} <math>v = \frac{\omega}{k}</math></center> | <center><math>k^2-\frac{\omega^2}{v^2}</math>{{tose}} <math>v = \frac{\omega}{k}</math></center> | ||
| + | |||
| + | En nuestro caso | ||
| + | |||
| + | <center><math>v = \frac{\omega}{k} = \frac{126}{0.314}\,\frac{\mathrm{cm}}{\mathrm{s}}\simeq 4\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | Otra forma de resolver este problema es descomponiendo esta onda estacionaria en suma de ondas viajeras. Tenemos en general que | ||
| + | |||
| + | <center><math>\mathrm{sen}\,(a)\cos(b) = \frac{1}{2}\,\mathrm{sen}\,(a+b)+\frac{1}{2}\mathrm{sen}\,(a-b)</math></center> | ||
| + | |||
| + | así que la señal del enunciado puede escribirse como | ||
| + | |||
| + | <center><math>A\cos(\omega t)\,\mathrm{sen}\,(kx) = \frac{A}{2}\,\mathrm{sen}\,(kx+\omega t)+\frac{A}{2}\,\mathrm{sen}\,(kx-\omega t)</math></center> | ||
| + | |||
| + | y a su vez podemos escribir esta combinación como | ||
| + | |||
| + | <center><math>\frac{A}{2}\,\mathrm{sen}\,\left(k\left(x+v t\right)\right)+\frac{A}{2}\,\mathrm{sen}\,(k(x-v t))=g(x+vt)+f(x-vt)</math>{{qquad}}<math>v=\frac{\omega}{k}</math></center> | ||
| + | |||
| + | esto es, que la señal equivale a la suma de dos ondas viajeras, una de las cuales va hacia la derecha y la otra hacia la izquierda, ambas con la misma velocidad <math>v = \omega/k</math>. | ||
| + | |||
| + | <center>[[Imagen:Estacio2.gif]]</center> | ||
| + | |||
[[Categoría:Problemas de movimiento ondulatorio]] | [[Categoría:Problemas de movimiento ondulatorio]] | ||
última version al 11:25 18 dic 2014
1 Enunciado
Una perturbación de una cuerda es de la forma
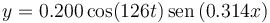
con x e y medidos en centímetros y t en segundos. Demuestre que esta función verifica la ecuación de ondas. ¿Qué velocidad le corresponde?
2 Solución
Hay que señalar que la forma de esta solución no es una señal que viaje ni hacia la derecha ni hacia la izquierda. Es lo que se denomina una onda estacionaria.Comenzamos escribiendo esta solución en la forma más general
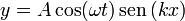
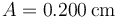
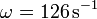
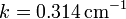
Se trata de demostrar que esta solución cumple una ecuación de la forma
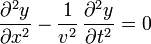
con v una constante que debemos calcular.
Hallamos las dos derivadas parciales segundas. Respecto al tiempo
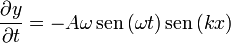
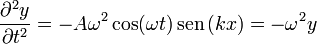
Respecto a la posición
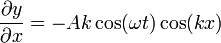
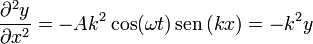
Sustituyendo en la ecuación de onda
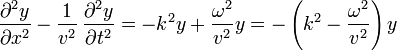
Esta expresión se anula en todo instante y para todos los puntos si la velocidad de las ondas es
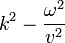

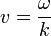
En nuestro caso
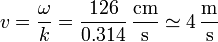
Otra forma de resolver este problema es descomponiendo esta onda estacionaria en suma de ondas viajeras. Tenemos en general que
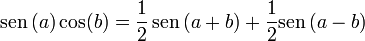
así que la señal del enunciado puede escribirse como
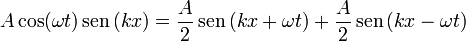
y a su vez podemos escribir esta combinación como
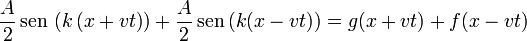
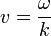
esto es, que la señal equivale a la suma de dos ondas viajeras, una de las cuales va hacia la derecha y la otra hacia la izquierda, ambas con la misma velocidad v = ω / k.