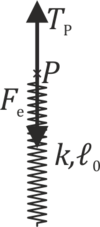Masa suspendida de un polipasto
De Laplace
| (7 ediciones intermedias no se muestran.) | |||
| Línea 24: | Línea 24: | ||
Supondremos inicialmente que las poleas no tienen masa ni momento de inercia, aunque la solución no es mucho más complicada suponiendo estos valores no nulos. | Supondremos inicialmente que las poleas no tienen masa ni momento de inercia, aunque la solución no es mucho más complicada suponiendo estos valores no nulos. | ||
| + | |||
| + | [[Archivo:polipasto-03.png|100px|right]] | ||
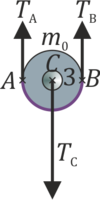
Sobre la polea 3 actúan la tensión del hilo en el punto A (a su izquierda), la del hilo en el punto opuesto B (que no tenemos por qué suponer que es igual a la tensión en A), su peso (por ahora despreciable) y la tensión de la varilla que une el centro C de la polea al bloque. | Sobre la polea 3 actúan la tensión del hilo en el punto A (a su izquierda), la del hilo en el punto opuesto B (que no tenemos por qué suponer que es igual a la tensión en A), su peso (por ahora despreciable) y la tensión de la varilla que une el centro C de la polea al bloque. | ||
| Línea 38: | Línea 40: | ||
<center><math>T_A=T_B=\frac{T_C}{2}</math></center> | <center><math>T_A=T_B=\frac{T_C}{2}</math></center> | ||
| + | |||
| + | [[Archivo:polipasto-04.png|100px|right]] | ||
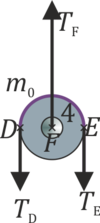
Para la polea 4 tenemos la tensión en el punto D a su izquierda y en el punto E a su derecha, así como la de la barra en el punto central F. Por ser el hilo inextensible, el módulo de la tensión en D es el mismo que en B. Por tanto | Para la polea 4 tenemos la tensión en el punto D a su izquierda y en el punto E a su derecha, así como la de la barra en el punto central F. Por ser el hilo inextensible, el módulo de la tensión en D es el mismo que en B. Por tanto | ||
<center><math>T_B=T_D=T_E=\frac{T_F}{2}</math></center> | <center><math>T_B=T_D=T_E=\frac{T_F}{2}</math></center> | ||
| + | |||
| + | [[Archivo:polipasto-02.png|100px|left]] | ||
Por último, en el punto P donde se unen el hilo y el resorte la segunda ley de Newton nos da | Por último, en el punto P donde se unen el hilo y el resorte la segunda ley de Newton nos da | ||
| Línea 50: | Línea 56: | ||
<center><math>T_A=T_B=T_D=T_E=T_P=k(\ell-\ell_0)\,</math></center> | <center><math>T_A=T_B=T_D=T_E=T_P=k(\ell-\ell_0)\,</math></center> | ||
| + | |||
| + | [[Archivo:polipasto-06.png|160px|right]] | ||
El bloque 2 está sometido al peso, a la tensión de la varilla que la une a la polea y a la fuerza del resorte. Por tanto | El bloque 2 está sometido al peso, a la tensión de la varilla que la une a la polea y a la fuerza del resorte. Por tanto | ||
| Línea 85: | Línea 93: | ||
<center><math>x_\mathrm{eq}=x_0+ \frac{mg}{9k}</math></center> | <center><math>x_\mathrm{eq}=x_0+ \frac{mg}{9k}</math></center> | ||
| + | |||
| + | y la tensión de cada hilo es | ||
| + | |||
| + | <center><math>T_A=T_B=T_D=T_E=k(\ell-\ell_0)=\frac{mg}{3}</math></center> | ||
==Frecuencia de las oscilaciones== | ==Frecuencia de las oscilaciones== | ||
| Línea 125: | Línea 137: | ||
siendo <math>\omega_0</math> la frecuencia propia del resorte. | siendo <math>\omega_0</math> la frecuencia propia del resorte. | ||
| + | El moviento que describe el bloque es uno armónico simple | ||
| + | |||
| + | <center><math>x=x_\mathrm{eq}+A\cos(\omega t+\phi)=x_0+\frac{mg}{9k}+A\cos(\omega t+\phi)\,</math></center> | ||
| + | |||
| + | La tensión de cada hilo varía también en el tiempo | ||
| + | |||
| + | <center><math>T_A=T_B=T_D=T_E=k(\ell-\ell_0)=3k(x-x_0)=\frac{mg}{3}+3kA\cos(\omega t+\phi)</math></center> | ||
| + | |||
| + | siendo su valor mínimo | ||
| + | |||
| + | <center><math>T_\mathrm{min}=\frac{mg}{3}-3kA</math></center> | ||
| + | |||
| + | Por ello, la amplitd máxima si no queremos que los hilos se destensen es | ||
| + | |||
| + | <center><math>A_\mathrm{max}=\frac{mg}{9k}</math></center> | ||
==Poleas no ideales== | ==Poleas no ideales== | ||
En el caso de que las poleas tengan masa y momento de inercia debemos incluirlas en los cálculos. Esto afecta tanto a la posición de equilibrio como la frecuencia de las oscilaciones. | En el caso de que las poleas tengan masa y momento de inercia debemos incluirlas en los cálculos. Esto afecta tanto a la posición de equilibrio como la frecuencia de las oscilaciones. | ||
| - | + | ;Ecuaciones para el bloque | |
Esta ecuación no cambia, aunque la tensión ahora podrá ser diferente | Esta ecuación no cambia, aunque la tensión ahora podrá ser diferente | ||
<center><math>-T_C-k(\ell-\ell_0)+mg=m\ddot{x}\,</math></center> | <center><math>-T_C-k(\ell-\ell_0)+mg=m\ddot{x}\,</math></center> | ||
| Línea 136: | Línea 163: | ||
<center><math>m\ddot{x}=-T_C-3k(x-x_0)+mg=m\ddot{x}\,</math></center> | <center><math>m\ddot{x}=-T_C-3k(x-x_0)+mg=m\ddot{x}\,</math></center> | ||
| - | + | ;Ecuaciones para la polea 3 | |
| - | Esta polea ahora tiene masa <math>m_0</math> y momento de inercia <math>I_0</math>. Las | + | Esta polea ahora tiene masa <math>m_0</math> y momento de inercia <math>I_0</math>. Las segunda ley de Newton dan, para esta polea |
<center><math>-T_A-T_B+T_C+m_0g=m_0\ddot{x}</math></center> | <center><math>-T_A-T_B+T_C+m_0g=m_0\ddot{x}</math></center> | ||
| - | Obsérvese que en el segundo miembro debe aparecer la aceleración del centro de la polea pero por estar unida rígidamente al bloque, ésta es también <math>\ddot{x}</math> | + | Obsérvese que en el segundo miembro debe aparecer la aceleración del centro de la polea pero por estar unida rígidamente al bloque, ésta es también <math>\ddot{x}</math>. |
| + | |||
| + | La ecuación para la rotación de esta polea es | ||
| + | |||
| + | <center><math>-T_Ar+T_Br=I_0\alpha_{31}\,</math></center> | ||
| + | |||
| + | Hay que relacionar la aceleración angular del disco con la lineal de su centro. Para ello observamos que esta polea rueda sobre el hilo que cuelga del techo, de forma que la velocidad del punto A es nula. | ||
| + | |||
| + | Cuando el centro desciende una distancia <math>\Delta x</math> el arco que avanza es <math>r\,\Delta\theta</math> en sentido horario, por tanto | ||
| + | |||
| + | <center><math>\Delta x = -r\,\Delta\theta\qquad \Rightarrow\qquad \dot{\theta}=-\frac{\dot{x}}{r}</math></center> | ||
| + | |||
| + | Más formalmente, este resultado se obtiene aplicando el campo de velocidades de un sólido | ||
| + | |||
| + | La velocidad del punto A es nula | ||
| + | |||
| + | <center><math>\vec{v}^A_{31}=\vec{0}</math></center> | ||
| + | |||
| + | y la del centro C, por la expresión del campo de velocidades | ||
| + | |||
| + | <center><math>\dot{x}\vec{\imath}=\vec{v}^C_{31}=\vec{v}^A_{31}+\vec{\omega}_{31}\times\overrightarrow{AB}=(\omega_{31}\vec{k})\times(r\vec{\jmath})=-\omega_{31}r\vec{\imath}</math></center> | ||
| + | |||
| + | De aquí | ||
| + | |||
| + | <center><math>\omega_{31}=-\frac{\dot{x}}{r}\qquad\Rightarrow \qquad \alpha_{31}=-\ddot{x}{r}</math></center> | ||
| + | |||
| + | Por tanto quedan las dos ecuaciones | ||
| + | |||
| + | <center><math>-T_A-T_B+T_C+m_0g=m_0\ddot{x}</math></center> | ||
| + | | ||
| + | <center><math>-T_A+T_B=-\frac{I_0}{r^2}\ddot{x}\,</math></center> | ||
| + | |||
| + | ;Ecuaciones para la polea 4 | ||
| + | Esta polea está fijada al techo, por lo que su centro permanece inmóvil | ||
| + | |||
| + | <center><math>T_D+T_Q-T_F+m_0g=0\,</math></center> | ||
| + | |||
| + | siendo | ||
| + | |||
| + | <math>T_D=T_B\,</math> | ||
| + | La ecuación de rotación de esta polea es | ||
| + | |||
| + | <center><math>T_Dr-T_Er=I_0\alpha_{41}\,</math></center> | ||
| + | |||
| + | La relación entre la aceleración angular de esta polea y la lineal del bloque la sacamos de la velocidad del punto D, que es la misma que la del punto B de la polea 3. | ||
| + | |||
| + | <center><math>\vec{v}^D_{41}=\vec{v}^B_{31}=\vec{\omega}_{31}\times\overrightarrow{AC}=2\dot{x}\vec{\imath}</math></center> | ||
| + | |||
| + | y por tanto | ||
| + | |||
| + | <center><math>\vec{v}^D_{41}=\overbrace{\vec{v}^F_{41}}^{=\vec{0}}+\vec{\omega}_{41}\times\overrightarrow{FD}=(\omega_{41}\vec{k})\times(-r\vec{\jmath})=\omega_{41}r\vec{\imath}</math></center> | ||
| + | |||
| + | De aquí | ||
| + | |||
| + | <center><math>\omega_{41}=\frac{2\dot{x}}{r}\qquad\Rightarrow\qquad \alpha_{41}=\frac{2\ddot{x}}{r}</math></center> | ||
| + | |||
| + | Queda entonces la ecuación de movimiento | ||
| + | |||
| + | <center><math>T_D-T_E=2\frac{I_0}{r^2}\ddot{x}</math></center> | ||
| + | |||
| + | ;Punto de contacto entre el hilo y el resorte | ||
| + | Por último, en este punto, que sigue sin tener masa, se cumple | ||
| + | |||
| + | <center><math>T_E-k(\ell-\ell_0)=0\qquad\Rightarrow\qquad T_E=3k(x-x_0)</math></center> | ||
| + | |||
| + | A partir de aquí, yendo en sentido inverso, vamos obteniendo sucesivamente las diferentes tensiones. En D | ||
| + | |||
| + | <center><math>T_D=T_E+2\frac{I_0}{r^2}\ddot{x}=3k(x-x_0)+2\frac{I_0}{r^2}\ddot{x}</math></center> | ||
| + | En B | ||
| + | <center><math>T_B=T_D=3k(x-x_0)+2\frac{I_0}{r^2}\ddot{x}</math></center> | ||
| + | En A | ||
| + | <center><math>T_A=T_B+\frac{I_0}{r^2}\ddot{x}=3k(x-x_0)+3\frac{I_0}{r^2}\ddot{x}</math></center> | ||
| + | En C | ||
| + | <center><math>T_C=T_A+T_B-m_0g+m_0\ddot{x}=6k(x-x_0)+5\frac{I_0}{r^2}\ddot{x}-m_0g+m_0\ddot{x}</math></center> | ||
| + | Con esta podemso completar ya la ecuación de movimiento para el bloque | ||
| + | |||
| + | <center><math>m\ddot{x}=mg-T_C-3k(x-x_0)=\left(m+m_0\right)g-\left(m_0+5\frac{I_0}{r^2}\right)\ddot{x}-9k(x-x_0)</math></center> | ||
| + | |||
| + | Agrupamos términos | ||
| + | |||
| + | <center><math>\left(m+m_0+5\frac{I_0}{r^2}\right)\ddot{x}=(m+m_0)g-9k(x-x_0)</math></center> | ||
| + | |||
| + | ;Nueva posición de equilibrio | ||
| + | Anulando la aceleración queda | ||
| + | |||
| + | <center><math>x_\mathrm{eq}=x_0+\frac{(m+m_0)g}{9k}</math></center> | ||
| + | |||
| + | ;Frecuencia de oscilación | ||
| + | Llevando esto a la ecuación de movimiento | ||
| + | |||
| + | <center><math>\ddot{x}=-\frac{9k}{m+m_0+5I_0/r^2}(x-x_\mathrm{eq})</math></center> | ||
| + | |||
| + | lo que da la frecuencia | ||
| + | |||
| + | <center><math>\omega= \sqrt{\frac{9k}{m+m_0+5I_0/r^2}}</math></center> | ||
| + | |||
| + | La posición del bloque sigue un movimiento armónico simple con la nueva frecuencia | ||
| + | |||
| + | <center><math>x=x_\mathrm{eq}+A\cos(\omega t+\phi)</math></center> | ||
| + | ;Tensiones en el hilo | ||
==Oscilaciones amortiguadas== | ==Oscilaciones amortiguadas== | ||
[[Categoría:Problemas de dinámica (CMR)]] | [[Categoría:Problemas de dinámica (CMR)]] | ||
última version al 15:52 20 may 2018
Contenido |
1 Enunciado
Un bloque “2” de masa m pende de un polipasto formado por dos poleas. La polea “3” tiene radio r y está unida rígidamente al bloque por una barra de longitud b. La polea “4” tiene el mismo radio y está fijada al techo “1” por otra barra de longitud b. Un hilo inextensible sin masa está atado al techo, pasa por la polea 3, luego por la 4 y está unida al bloque mediante un resorte de constante k y longitud natural 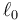 . La longitud del hilo es tal que en ausencia de peso del bloque, el muelle estaría en su longitud natural y el hilo estirado pero sin tensión.
. La longitud del hilo es tal que en ausencia de peso del bloque, el muelle estaría en su longitud natural y el hilo estirado pero sin tensión.
Se cuelga verticalmente el sistema.
- Suponiendo que las poleas no tienen masa, halle la posición de equilibrio del bloque, heq, medida desde el techo. ¿Cuánto vale la tensión del hilo en ese estado?
- Suponiendo que el bloque que se desplaza verticalmente una cantidad A respecto de la posición de equilibrio, determine la frecuencia de las oscilaciones que describe el bloque. ¿Cuánto debe ser el valor máximo de la amplitud si no se quiere que el hilo se destense?
- Suponga ahora que las dos poleas son cilindros macizos de masa m0, con su correspondiente momento de inercia. ¿Cuánto vale en ese caso la frecuencia de las oscilaciones?
- Suponga ahora que el bloque está conectado a un amortiguador de constante γ ¿Cuál es la ecuación de movimiento del bloque en ese caso?

2 Posición de equilibrio
Para estudiar este sistema, lo más sistemático consiste en analizar cada sólido por separado, aplicando los diagramas de cuerpo libre correspondiente.
En este caso tenemos 4 sólidos.
- El techo, que es inmóvil y al cual ligamos un sistema de referencia fijo en el cual eje OX es vertical y hacia abajo, el OY es horizontal en el plano de movimiento y el OZ es horizontal perpendicular a este plano.
- El bloque, que experimenta traslación respecto al 1, pero no rotación. Esto es, se comporta como una partícula.
- La polea inferior, que experimenta tanto traslación como rotación.
- La polea superior, que experimenta solo rotación pero no traslación respecto al 1.
Además de estos, conviene imaginar una partícula "5" sin masa en el punto en el que se unen el cable inextensible con el resorte, ya que hay que relacionar la tensión del hilo con la fuerza elástica ejercida por el resorte.
Para establecer la posición de equilibrio debemos imponer que la suma de fuerzas y de momentos sea nula sobre cada uno de los sólidos.
Supondremos inicialmente que las poleas no tienen masa ni momento de inercia, aunque la solución no es mucho más complicada suponiendo estos valores no nulos.
Sobre la polea 3 actúan la tensión del hilo en el punto A (a su izquierda), la del hilo en el punto opuesto B (que no tenemos por qué suponer que es igual a la tensión en A), su peso (por ahora despreciable) y la tensión de la varilla que une el centro C de la polea al bloque.
Con el sistema de ejes considerado, todas las fuerzas van en el sentido del eje OX, por lo que queda la ecuación escalar
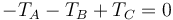
mientras que la ecuación de los momentos para esta polea es
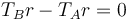
Lo cual nos da efectivamente que
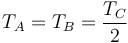
Para la polea 4 tenemos la tensión en el punto D a su izquierda y en el punto E a su derecha, así como la de la barra en el punto central F. Por ser el hilo inextensible, el módulo de la tensión en D es el mismo que en B. Por tanto
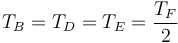
Por último, en el punto P donde se unen el hilo y el resorte la segunda ley de Newton nos da
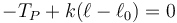
siendo la tensión del hilo en P la misma que en E (y por tanto, que en A, B y D).
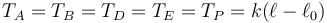
El bloque 2 está sometido al peso, a la tensión de la varilla que la une a la polea y a la fuerza del resorte. Por tanto
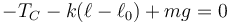
sustituyendo aquí la tensión de la varilla
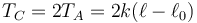
nos queda
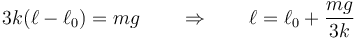
El resorte se estira un tercio de lo que lo haría si el bloque colgara solo de él. A su vez, la fuerza que soporta la varilla es 2/3 del peso y el muelle 1/3 del peso. La tensión del hilo es también 1/3 del peso.
La posición respecto al techo depende de la longitud del cable. Si en ausencia de masa del bloque el muelle tendría una longitud 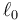 y el bloque estaría a una distancia x0 del techo quiere esto decir que el hilo mide
y el bloque estaría a una distancia x0 del techo quiere esto decir que el hilo mide
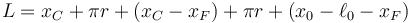
como

Nos da una longitud
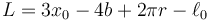
Esta cantidad es constante. Por tanto, en todo momento se va a cumplir

es decir, lo que desciende el bloque es la tercera parte de lo que se elonga el muelle.
En el equilibrio tendremos que
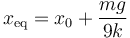
y la tensión de cada hilo es
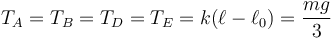
3 Frecuencia de las oscilaciones
En el caso de que el bloque no se halle en la posición de equilibrio, debemos aplicar la segunda ley de Newton para determinar su movimiento.
Si las poleas y el hilo son ideales, no tienen inercia alguna, por lo que sigue cumpliéndose
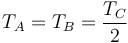
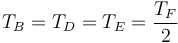
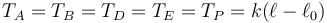
y solo cambia la ecuación
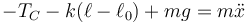
es decir, equivale a sustituir g por 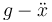 . Por tanto llegamos a
. Por tanto llegamos a
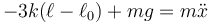
Como se sigue cumpliendo la relación geométrica
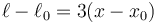
resulta la ecuación de movimiento
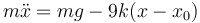
Introducimos aquí la posición de equilibrio con peso
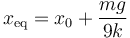
y obtenemos finalmente
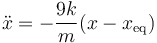
es decir, el bloque oscila con una frecuencia
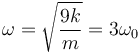
siendo ω0 la frecuencia propia del resorte.
El moviento que describe el bloque es uno armónico simple
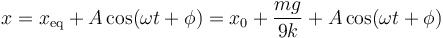
La tensión de cada hilo varía también en el tiempo
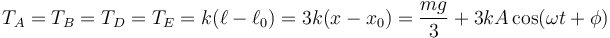
siendo su valor mínimo
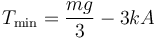
Por ello, la amplitd máxima si no queremos que los hilos se destensen es
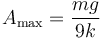
4 Poleas no ideales
En el caso de que las poleas tengan masa y momento de inercia debemos incluirlas en los cálculos. Esto afecta tanto a la posición de equilibrio como la frecuencia de las oscilaciones.
- Ecuaciones para el bloque
Esta ecuación no cambia, aunque la tensión ahora podrá ser diferente
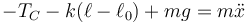
y, en función de x
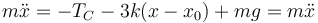
- Ecuaciones para la polea 3
Esta polea ahora tiene masa m0 y momento de inercia I0. Las segunda ley de Newton dan, para esta polea
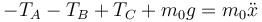
Obsérvese que en el segundo miembro debe aparecer la aceleración del centro de la polea pero por estar unida rígidamente al bloque, ésta es también 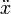 .
.
La ecuación para la rotación de esta polea es
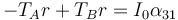
Hay que relacionar la aceleración angular del disco con la lineal de su centro. Para ello observamos que esta polea rueda sobre el hilo que cuelga del techo, de forma que la velocidad del punto A es nula.
Cuando el centro desciende una distancia Δx el arco que avanza es  en sentido horario, por tanto
en sentido horario, por tanto
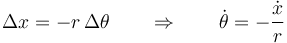
Más formalmente, este resultado se obtiene aplicando el campo de velocidades de un sólido
La velocidad del punto A es nula
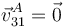
y la del centro C, por la expresión del campo de velocidades
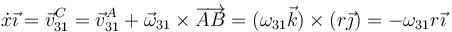
De aquí
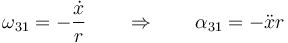
Por tanto quedan las dos ecuaciones
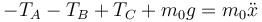
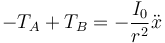
- Ecuaciones para la polea 4
Esta polea está fijada al techo, por lo que su centro permanece inmóvil
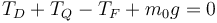
siendo
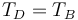 La ecuación de rotación de esta polea es
La ecuación de rotación de esta polea es
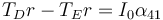
La relación entre la aceleración angular de esta polea y la lineal del bloque la sacamos de la velocidad del punto D, que es la misma que la del punto B de la polea 3.
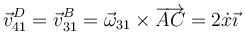
y por tanto
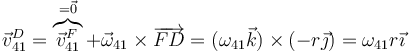
De aquí

Queda entonces la ecuación de movimiento
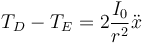
- Punto de contacto entre el hilo y el resorte
Por último, en este punto, que sigue sin tener masa, se cumple
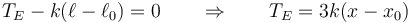
A partir de aquí, yendo en sentido inverso, vamos obteniendo sucesivamente las diferentes tensiones. En D
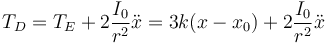
En B
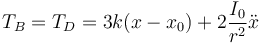
En A
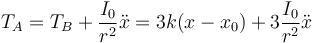
En C
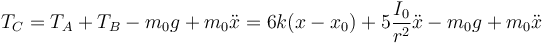
Con esta podemso completar ya la ecuación de movimiento para el bloque
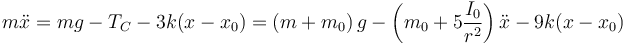
Agrupamos términos
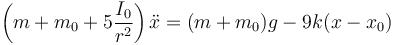
- Nueva posición de equilibrio
Anulando la aceleración queda
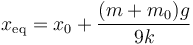
- Frecuencia de oscilación
Llevando esto a la ecuación de movimiento
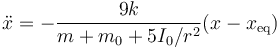
lo que da la frecuencia
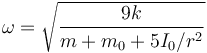
La posición del bloque sigue un movimiento armónico simple con la nueva frecuencia
- Tensiones en el hilo