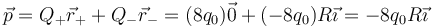Esfera cargada con hueco relleno (GIE)
De Laplace
| (11 ediciones intermedias no se muestran.) | |||
| Línea 10: | Línea 10: | ||
==Campo eléctrico== | ==Campo eléctrico== | ||
| - | El campo eléctrico se halla por superposición. | + | El campo eléctrico se halla por superposición. |
| - | + | Tratamos la esfera con el hueco relleno como la suma de: | |
| - | y una | + | una esfera completa de radio 2R y densidad de carga <math>\rho_1</math> superpuesta con una de radio R y densidad <math>\rho_2</math>. Se trata en primer lugar de determinar <math>\rho_1</math> y <math>\rho_2</math>. |
| - | |||
| - | + | <center>[[Archivo:dos-esferas-cargadas-01.png|300px|middle]]=[[Archivo:dos-esferas-cargadas-02.png|300px|middle]]+[[Archivo:dos-esferas-cargadas-03.png|300px|middle]]</center> | |
| - | + | * Una esfera de radio 2R centrada en O y densidad de carga <math>\rho_1</math>. | |
| - | * Una esfera de radio | + | * Una esfera de radio R, centrada en A y de densidad de carga math>\rho_1</math> |
| - | + | ||
| - | + | ||
| - | + | Consideremos en primer lugar la región de carga positiva, que podemos llamar “luna”. En esta “luna” solo tenemos la densidad de carga <math>\rho_1</math>, siendo la carga total <math>+7q_0</math>. El volumen de esta región es el de la esfera completa menos el del hueco. Por tanto, en esta región se cumple | |
| - | + | ||
| - | <center><math>\ | + | <center><math>\rho_1\left(\frac{4\pi}{3}(2R)^3-\frac{4\pi}{3}R^3\right)= +7q_0 \qquad\Rightarrow\qquad \rho_1=\frac{3q_0}{4\pi R^3}</math></center> |
| - | + | ||
| - | < | + | Para el hueco rellenos tenemos la superposición de <math>\rho_1</math> y <math>\rho_2</math>. La carga total de esta región es <math>-7q_0</math>. Por ello se cumple |
| + | |||
| + | <center><math>\rho_1\left(\frac{4\pi}{3}R^3\right)+\rho_2\left(\frac{4\pi}{3}R^3\right)=-7q_0</math></center> | ||
| + | |||
| + | Sustituimos aquí el valor de <math>\rho_1</math> calculado antes y queda | ||
| + | |||
| + | <center><math>\rho_2=-\frac{6q_0}{\pi R^3}=-8\rho_1</math></center> | ||
| + | |||
| + | Nótese que el valor de la carga total de la esfera de radio 2R cargada positivamente no es <math>+7q_0</math> sino | ||
| + | |||
| + | <center><math>Q_+=\rho_1 \frac{4\pi}{3}(2R)^3 = +8q_0</math></center> | ||
| + | |||
| + | y la de la esfera de carga negativa | ||
| + | |||
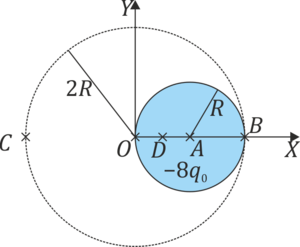
| + | <center><math>Q_-=\rho_2 \frac{4\pi}{3}(R)^3 = -8q_0</math></center> | ||
| + | |||
| + | A partir de aquí hallamos el campo eléctrico. | ||
El campo creado por una esfera de radio a cargada uniformemente en volumen con una carga Q es, para todo punto del espacio | El campo creado por una esfera de radio a cargada uniformemente en volumen con una carga Q es, para todo punto del espacio | ||
| Línea 47: | Línea 58: | ||
El punto O es el centro de la esfera positiva (por lo que el campo de ésta es nulo en este punto) y está en el borde de la esfera negativa, a una distancia R de su centro. El unitario radial desde el centro de la esfera negativa es <math>-\vec{\imath}</math>. Por tanto | El punto O es el centro de la esfera positiva (por lo que el campo de ésta es nulo en este punto) y está en el borde de la esfera negativa, a una distancia R de su centro. El unitario radial desde el centro de la esfera negativa es <math>-\vec{\imath}</math>. Por tanto | ||
| - | <center><math>\vec{E}_O=\vec{0}+\frac{Q_-}{4\pi\varepsilon_0 R^2}(-\vec{\imath})=\frac{2q_0}{\pi\ | + | <center><math>\vec{E}_O=\vec{0}+\frac{Q_-}{4\pi\varepsilon_0 R^2}(-\vec{\imath})=\frac{2q_0}{\pi\varepsilon_0R^2}\vec{\imath}</math></center> |
===En el punto B=== | ===En el punto B=== | ||
El punto B se halla en el borde de ambas esferas, a distancias 2R y R de sus centros respectivos, siendo el unitario radial <math>+\vec{\imath}</math> para ambas. Esto nos da el campo | El punto B se halla en el borde de ambas esferas, a distancias 2R y R de sus centros respectivos, siendo el unitario radial <math>+\vec{\imath}</math> para ambas. Esto nos da el campo | ||
| Línea 57: | Línea 68: | ||
<center><math>\vec{E}_B=\frac{Q_+}{4\pi\varepsilon_0(2R)^2}(-\vec{\imath})+\frac{Q_-}{4\pi\varepsilon_0(3R)^2}(-\vec{\imath})=\left(\frac{8q_0}{16\pi\varepsilon_0 R^2}-\frac{8q_0}{36\pi\varepsilon_0R^2}\right)(-\vec{\imath})=-\frac{5q_0}{18\pi\varepsilon_0R^2}\vec{\imath}</math></center> | <center><math>\vec{E}_B=\frac{Q_+}{4\pi\varepsilon_0(2R)^2}(-\vec{\imath})+\frac{Q_-}{4\pi\varepsilon_0(3R)^2}(-\vec{\imath})=\left(\frac{8q_0}{16\pi\varepsilon_0 R^2}-\frac{8q_0}{36\pi\varepsilon_0R^2}\right)(-\vec{\imath})=-\frac{5q_0}{18\pi\varepsilon_0R^2}\vec{\imath}</math></center> | ||
| + | ===En el punto A=== | ||
| + | El punto A se encuentra en el centro de la esfera negativa, por lo que el campo debida a ésta es nulo. A se halla en el interior de la esfera positiva, por lo que hay que emplear la expresión del campo interior para esta esfera | ||
| + | <center><math>\vec{E}_A=\frac{Q_+}{4\pi\varepsilon_0(2R)^3}R\vec{\imath}+\vec{0}=\frac{q_0}{4\pi\varepsilon_0R^2}\vec{\imath}</math></center> | ||
| + | |||
| + | ===En el punto D=== | ||
| + | El punto D es interior a ambas esferas. El vector unitario radial es <math>+\vec{\imath}</math> para la esfera positiva y <math>-\vec{\imath}</math> para la negativa. D se halla a una distancia (R/2) de cada uno de los centros. Por tanto | ||
| + | |||
| + | <center><math>\vec{E}_D=\frac{Q_+}{4\pi\varepsilon_0(2R)^3}\left(\frac{R}{2}\right)\vec{\imath}+\frac{Q_-}{4\pi\varepsilon_0R^3}\left(\frac{R}{2}\right)(-\vec{\imath})=\frac{3q_0}{2\pi\varepsilon_0R^2}\vec{\imath}</math></center> | ||
==Trabajo de B a C== | ==Trabajo de B a C== | ||
| + | El trabajo para mover una carga q desde B a C lo podemos mediante la diferencia de potencial entre ambos puntos | ||
| + | |||
| + | <center><math>W_{B\to C}=q(V(C)-V(B))\,</math></center> | ||
| + | |||
| + | El potencial en cada punto es la suma de los debidos a las dos esferas. | ||
| + | |||
| + | A su vez, ambos puntos, B y C se hallan en el exterior de las dos esferas, por lo que el potencial de cada una equivale al de una carga puntual situada en su centro. | ||
| + | |||
| + | El trabajo vale por consiguiente | ||
| + | |||
| + | <center><math>W_{B\to C} =q((V_{+}(C)+V_-(C))-(V_+(B)+V_-(B)))=q\left(\left(\frac{8q_0}{4\pi\varepsilon_0(2R)}-\frac{8q_0}{4\pi\varepsilon_0(3R)}\right)+\left(\frac{8q_0}{4\pi\varepsilon_0(2R)}-\frac{8q_0}{4\pi\varepsilon_0(R)}\right)\right)=\frac{4qq_0}{3\pi\varepsilon_0R}</math></center> | ||
| + | |||
==Trabajo de B a O== | ==Trabajo de B a O== | ||
| + | De manera similar se halla el trabajo para ir de B a O, aunque en este caso el cálculo del potencial es algo más complicado. | ||
| + | |||
| + | <center><math>W_{B\to O}=q(V(O)-V(B))=q((V_{+}(O)+V_-(O))-(V_+(B)+V_-(B)))\,</math></center> | ||
| + | De las dos esferas, la de carga negativa no contribuye ya que los puntos O y B se hallan a la misma distancia de su centro | ||
| + | |||
| + | <center><math>q(V_-(O)-V_-(B))=0\,</math></center> | ||
| + | |||
| + | Para la esfera positiva, el potencial en el punto B es, como antes vimos, el de una carga puntual. En el punto O, en cambio, hay que usar la expresión del potencial en el [[Potencial_el%C3%A9ctrico_debido_a_una_esfera_maciza#Potencial_en_el_centro_de_la_esfera|centro de una esfera cargada]] o bien integrar el campo eléctrico. Empleando este segundo camino queda | ||
| + | |||
| + | <center><math>W_{B\to O}=q(V_+(O)-V_+(B))=-q\int_B^O \vec{E}_+\cdot\mathrm{d}\vec{r}=-q\int_{2R}^0\frac{8q_0}{4\pi\varepsilon_0(2R)^3}r\,\mathrm{d}r=-\frac{qq_0}{4\pi\varepsilon_0 R^3}\int_{2R}^0 r\,\mathrm{d}r=\frac{qq_0}{2\pi\varepsilon_0R}</math></center> | ||
==Momento dipolar== | ==Momento dipolar== | ||
| + | Visto desde el exterior, el sistema equivale a una carga <math>+8q_0</math> situada en O y una <math>-8q_0</math> situada en A. El momento dipolar de esta distribución es | ||
| + | |||
| + | <center><math>\vec{p}=Q_+\vec{r}_++Q_-\vec{r}_-=(8q_0)\vec{0}+(-8q_0)R\vec{\imath}=-8q_0R\vec{\imath}</math></center> | ||
[[Categoría:Problemas de electrostática en el vacío]] | [[Categoría:Problemas de electrostática en el vacío]] | ||
última version al 15:25 30 abr 2018
Contenido |
1 Enunciado
Una esfera de radio 2R posee un hueco también esférico de radio R cuyo centro se encuentra a una distancia R del centro de la esfera grande. La esfera grande almacena una carga + 7q0 distribuida uniformemente en su volumen, mientras que en el hueco hay una carga − 7q0 también distribuida uniformemente.

- Halle el campo eléctrico en los puntos O, B, C, A y D marcados en la figura. A es el centro de la esfera negativa y D es equidistante de O y A.
- Calcule el trabajo para mover una carga puntual q desde el punto B al punto C, diametralmente opuesto.
- Calcule el trabajo para mover la misma carga desde el punto B hasta el punto O.
- En puntos exteriores a la esfera y alejados de ella, el sistema se ve como un dipolo. ¿Cuánto vale el momento dipolar eléctrico de este dipolo?
2 Campo eléctrico
El campo eléctrico se halla por superposición.
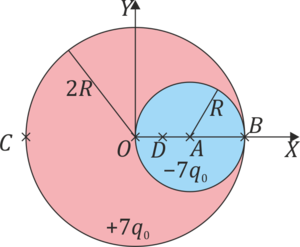
Tratamos la esfera con el hueco relleno como la suma de:
una esfera completa de radio 2R y densidad de carga ρ1 superpuesta con una de radio R y densidad ρ2. Se trata en primer lugar de determinar ρ1 y ρ2.
 =
=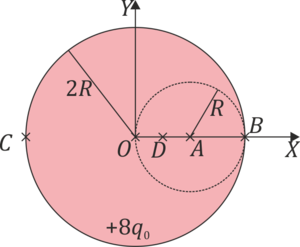 +
+
- Una esfera de radio 2R centrada en O y densidad de carga ρ1.
- Una esfera de radio R, centrada en A y de densidad de carga math>\rho_1</math>
Consideremos en primer lugar la región de carga positiva, que podemos llamar “luna”. En esta “luna” solo tenemos la densidad de carga ρ1, siendo la carga total + 7q0. El volumen de esta región es el de la esfera completa menos el del hueco. Por tanto, en esta región se cumple

Para el hueco rellenos tenemos la superposición de ρ1 y ρ2. La carga total de esta región es − 7q0. Por ello se cumple
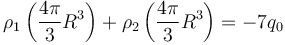
Sustituimos aquí el valor de ρ1 calculado antes y queda
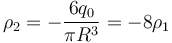
Nótese que el valor de la carga total de la esfera de radio 2R cargada positivamente no es + 7q0 sino
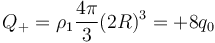
y la de la esfera de carga negativa
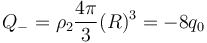
A partir de aquí hallamos el campo eléctrico.
El campo creado por una esfera de radio a cargada uniformemente en volumen con una carga Q es, para todo punto del espacio
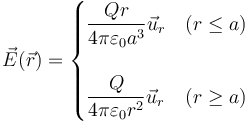
siendo r la distancia al centro de la esfera y 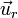 el unitario radial desde el centro de la esfera
el unitario radial desde el centro de la esfera
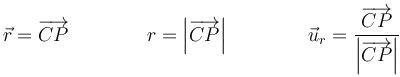
A partir de aquí, podemos hallar el campo en cada punto
2.1 En el punto O
El punto O es el centro de la esfera positiva (por lo que el campo de ésta es nulo en este punto) y está en el borde de la esfera negativa, a una distancia R de su centro. El unitario radial desde el centro de la esfera negativa es 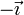 . Por tanto
. Por tanto
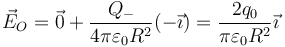
2.2 En el punto B
El punto B se halla en el borde de ambas esferas, a distancias 2R y R de sus centros respectivos, siendo el unitario radial 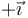 para ambas. Esto nos da el campo
para ambas. Esto nos da el campo
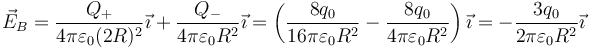
2.3 En el punto C
El punto C se halla en el exterior de ambas esferas, a distancias 2R y 3R de cada centro, siendo el unitario radial 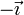 en ambos casos
en ambos casos
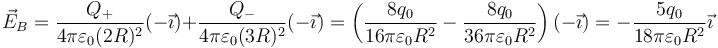
2.4 En el punto A
El punto A se encuentra en el centro de la esfera negativa, por lo que el campo debida a ésta es nulo. A se halla en el interior de la esfera positiva, por lo que hay que emplear la expresión del campo interior para esta esfera
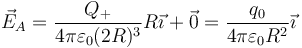
2.5 En el punto D
El punto D es interior a ambas esferas. El vector unitario radial es 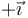 para la esfera positiva y
para la esfera positiva y 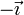 para la negativa. D se halla a una distancia (R/2) de cada uno de los centros. Por tanto
para la negativa. D se halla a una distancia (R/2) de cada uno de los centros. Por tanto
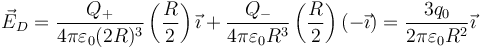
3 Trabajo de B a C
El trabajo para mover una carga q desde B a C lo podemos mediante la diferencia de potencial entre ambos puntos
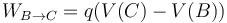
El potencial en cada punto es la suma de los debidos a las dos esferas.
A su vez, ambos puntos, B y C se hallan en el exterior de las dos esferas, por lo que el potencial de cada una equivale al de una carga puntual situada en su centro.
El trabajo vale por consiguiente

4 Trabajo de B a O
De manera similar se halla el trabajo para ir de B a O, aunque en este caso el cálculo del potencial es algo más complicado.

De las dos esferas, la de carga negativa no contribuye ya que los puntos O y B se hallan a la misma distancia de su centro
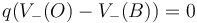
Para la esfera positiva, el potencial en el punto B es, como antes vimos, el de una carga puntual. En el punto O, en cambio, hay que usar la expresión del potencial en el centro de una esfera cargada o bien integrar el campo eléctrico. Empleando este segundo camino queda
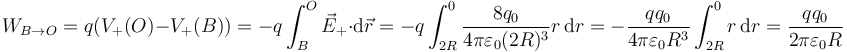
5 Momento dipolar
Visto desde el exterior, el sistema equivale a una carga + 8q0 situada en O y una − 8q0 situada en A. El momento dipolar de esta distribución es