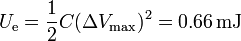Ruptura dieléctrica
De Laplace
(→Condensador parcialmente lleno) |
|||
| (10 ediciones intermedias no se muestran.) | |||
| Línea 4: | Línea 4: | ||
# Suponga que entre dos placas planas y paralelas de sección circular de diámetro ''D'' = 26 cm, entre las cuales se encaja una lámina de metacrilato de grosor ''a'' = 2 mm, cuya permitividad es ε<sub><i>r</i></sub> = 3.40 y el campo de ruptura es ''E''<sub><i>c</i></sub> = 30 kV/mm. Halle la máxima carga que puede almacenar este condensador. | # Suponga que entre dos placas planas y paralelas de sección circular de diámetro ''D'' = 26 cm, entre las cuales se encaja una lámina de metacrilato de grosor ''a'' = 2 mm, cuya permitividad es ε<sub><i>r</i></sub> = 3.40 y el campo de ruptura es ''E''<sub><i>c</i></sub> = 30 kV/mm. Halle la máxima carga que puede almacenar este condensador. | ||
# Suponga que, en el caso anterior las placas no están en contacto con el metacrilato, sino que hay un espacio de 1 mm a cada lado lleno de aire, cuyo campo de ruptura es 3 kV/mm, ¿cuál es en ese caso la carga máxima? | # Suponga que, en el caso anterior las placas no están en contacto con el metacrilato, sino que hay un espacio de 1 mm a cada lado lleno de aire, cuyo campo de ruptura es 3 kV/mm, ¿cuál es en ese caso la carga máxima? | ||
| - | # Si lo que tenemos es un cable coaxial RG-58/U de radio interior ''a'' = 0.9 mm y exterior ''b'' = 3.8 mm, entre las cuales hay polietileno con permitividad ε<sub><i>r</i></sub> = 2.3 y campo de ruptura ''E''<sub><i>c</i></sub> = 0.5 kV/mm, ¿cuál es la mayor diferencia de potencial que se puede establecer entre el núcleo y el conductor exterior? | + | # Si lo que tenemos es un cable coaxial RG-58/U de radio interior ''a'' = 0.9 mm y exterior ''b'' = 3.8 mm, entre las cuales hay polietileno con permitividad ε<sub><i>r</i></sub> = 2.3 y campo de ruptura ''E''<sub><i>c</i></sub> = 0.5 kV/mm, |
| + | ## ¿cuál es la mayor diferencia de potencial que se puede establecer entre el núcleo y el conductor exterior? | ||
| + | ## Si tenemos 2 m de cable RG-58/U ¿cuánto vale la carga máxima que se almacena en este condensador? | ||
| + | ## ¿Cuánto vale la energía máxima almacenada en estos 2 metros de cable? | ||
| - | + | ==Condensador totalmente relleno== | |
| - | + | ||
Si el dieléctrico llena completamente el espacio entre las placas, el campo eléctrico es idéntico al que habría en vacío | Si el dieléctrico llena completamente el espacio entre las placas, el campo eléctrico es idéntico al que habría en vacío | ||
| Línea 22: | Línea 24: | ||
Un aspecto interesante de este resultado es que no depende de la distancia entre las placas. | Un aspecto interesante de este resultado es que no depende de la distancia entre las placas. | ||
| - | + | ==Condensador parcialmente lleno== | |
Cuando tenemos dos capas de aire (de permitividad <math>\varepsilon_0</math>) el problema se complica porque el campo crítico es diferente en cada medio y también lo es el valor del campo que existe en cada región. | Cuando tenemos dos capas de aire (de permitividad <math>\varepsilon_0</math>) el problema se complica porque el campo crítico es diferente en cada medio y también lo es el valor del campo que existe en cada región. | ||
| - | Operando como en el problema “[[ | + | Operando como en el problema “[[Condensador con dos capas de dieléctrico]]”, tenemos tres valores del campo, uniformes en cada región, que verifican |
<center> | <center> | ||
<math>E_1b+E_2a+E_3b = \Delta V\,</math>{{qquad}}{{qquad}}<math>\varepsilon_0 E_1 = \varepsilon E_2\,</math>{{qquad}}{{qquad}} <math>\varepsilon E_2 = \varepsilon_0E_3\,</math></center> | <math>E_1b+E_2a+E_3b = \Delta V\,</math>{{qquad}}{{qquad}}<math>\varepsilon_0 E_1 = \varepsilon E_2\,</math>{{qquad}}{{qquad}} <math>\varepsilon E_2 = \varepsilon_0E_3\,</math></center> | ||
| Línea 33: | Línea 35: | ||
Resolviendo este sistema de ecuaciones obtenemos | Resolviendo este sistema de ecuaciones obtenemos | ||
<center> | <center> | ||
| - | <math>E_1 = E_3 = \frac{\varepsilon \Delta V}{2b\varepsilon+a\varepsilon_0}</math>{{qquad}}{{qquad}}<math>E_2 = \frac{\varepsilon_0 \Delta V}{2b\varepsilon+a\varepsilon_0}</math></center> | + | <math>E_1 = E_3 = \frac{\varepsilon\,\Delta V}{2b\varepsilon+a\varepsilon_0}</math>{{qquad}}{{qquad}}<math>E_2 = \frac{\varepsilon_0\, \Delta V}{2b\varepsilon+a\varepsilon_0}</math></center> |
| + | |||
| + | Para una diferencia de potencial dada, el campo es más intenso en la capa de aire (porque <math>\varepsilon> \varepsilon_0</math>), donde además el campo de ruptura es menor. Por tanto, la condición para que salte la chispa es que | ||
| + | |||
| + | <center><math>E_1 = E_c(\mathrm{aire})\,</math>{{tose}}<math>\Delta V_\mathrm{max} = \frac{(2b\varepsilon +a\varepsilon_0)E_c(\mathrm{aire})}{\varepsilon}=7.8\,\mathrm{kV}</math></center> | ||
| + | |||
| + | bastante inferior al anterior, pues el campo de ruptura en el aire es 10 veces más pequeño que en el metacrilato. | ||
| + | |||
| + | La capacidad de este condensador es | ||
| + | |||
| + | <center><math>C = \frac{\varepsilon_0\varepsilon S}{2b\varepsilon+a\varepsilon_0}=0.18\,\mathrm{nF}</math></center> | ||
| + | |||
| + | y la carga máxima posible | ||
| + | |||
| + | <center><math>Q_\mathrm{max}=C\,\Delta V_\mathrm{max}= \varepsilon_0 SE_c(\mathrm{aire}) = 1.4\,\mu\mathrm{C}</math></center> | ||
| + | |||
| + | Vemos que en el resultado final no aparece el metacrilato. Esto se entiende observando que el sistema equivale a tres condensadores puestos en serie, y por tanto los tres cargados en la misma magnitud. Cuando salta la chispa lo hace en el que tenga el menor campo critico, que es uno de los dos llenos de aire. Es la carga de este condensador la máxima posible, y por ello no aparece el condensador lleno de metacrilato. | ||
| + | |||
| + | ==Cable coaxial== | ||
| + | ===Máxima diferencia de potencial=== | ||
| + | En el caso de un cable coaxial tenemos que el campo no tiene el mismo valor en todos los puntos, ya que el potencial varía con la posición como en el caso de un [[condensador coaxial]] | ||
| + | |||
| + | <center><math>\phi = -\frac{V_0 \ln(\rho/b)}{\ln(b/a)}</math></center> | ||
| + | |||
| + | El campo entre los dos cilindros (y por tanto en el dieléctrico) vale | ||
| + | |||
| + | <center><math>\mathbf{E}=-\nabla\phi = \frac{V_0}{\rho \ln(b/a)}\mathbf{u}_\rho</math></center> | ||
| + | |||
| + | Este campo es más intenso en las proximidades del cilindro interior y más débil junto al cilindro exterior. Para que salte la chispa debe producirse la ruptura en todo el dieléctrico, por lo que la condición la da el que el campo mínimo coincida con el de ruptura. | ||
| + | |||
| + | <center><math>E(b) = \frac{V_0}{b \ln(b/a)} = E_c{{\to}}V_0 = E_c b \ln\left(\frac{b}{a}\right) = 2700\,\mathrm{V}</math></center> | ||
| + | |||
| + | En este apartado, la presencia del dieléctrico es importante, no sólo porque de su naturaleza depende el campo de ruptura, sino porque el comportamiento de un condensador coaxial lleno de aire es diferente del caso relleno de un dieléctrico sólido. En el aire puede producirse el [http://en.wikipedia.org/wiki/Corona_discharge efecto corona] en el que la descarga se produce en la región de campo más intenso, junto al hilo central. | ||
| + | |||
| + | ===Máxima carga=== | ||
| + | Una vez que tenemos la máxima diferencia de potencial, la carga almacenada en el condensador es inmediato | ||
| + | |||
| + | <center><math>Q_\mathrm{max} = C\,\Delta V_\mathrm{max}</math></center> | ||
| + | |||
| + | siendo la capacidad de este [[condensador coaxial]] | ||
| + | |||
| + | <center><math>C = \frac{2\pi\varepsilon L}{\ln(b/a)} = 177\,\mathrm{pF}</math></center> | ||
| + | |||
| + | y la carga máxima | ||
| + | |||
| + | <center><math>Q_\mathrm{max}= 0.48\,\mu\mathrm{C}</math></center> | ||
| + | |||
| + | ===Máxima energía=== | ||
| + | De forma similar se halla la energía máxima que almacena el condensador | ||
| + | |||
| + | <center><math>U_\mathrm{e}= \frac{1}{2}C(\Delta V_\mathrm{max})^2 = 0.66\,\mathrm{mJ}</math></center> | ||
| + | |||
| - | |||
[[Categoría:Problemas de materiales dieléctricos]] | [[Categoría:Problemas de materiales dieléctricos]] | ||
última version al 16:25 30 jun 2009
Contenido |
1 Enunciado
La ruptura dieléctrica se produce cuando el campo eléctrico entre dos conductores supera un valor crítico Ec, saltando una chispa en el vacío, o quemando el dieléctrico que pueda haber en medio. Esto limita la carga que se puede almacenar en las placas de un condensador.
- Suponga que entre dos placas planas y paralelas de sección circular de diámetro D = 26 cm, entre las cuales se encaja una lámina de metacrilato de grosor a = 2 mm, cuya permitividad es εr = 3.40 y el campo de ruptura es Ec = 30 kV/mm. Halle la máxima carga que puede almacenar este condensador.
- Suponga que, en el caso anterior las placas no están en contacto con el metacrilato, sino que hay un espacio de 1 mm a cada lado lleno de aire, cuyo campo de ruptura es 3 kV/mm, ¿cuál es en ese caso la carga máxima?
- Si lo que tenemos es un cable coaxial RG-58/U de radio interior a = 0.9 mm y exterior b = 3.8 mm, entre las cuales hay polietileno con permitividad εr = 2.3 y campo de ruptura Ec = 0.5 kV/mm,
- ¿cuál es la mayor diferencia de potencial que se puede establecer entre el núcleo y el conductor exterior?
- Si tenemos 2 m de cable RG-58/U ¿cuánto vale la carga máxima que se almacena en este condensador?
- ¿Cuánto vale la energía máxima almacenada en estos 2 metros de cable?
2 Condensador totalmente relleno
Si el dieléctrico llena completamente el espacio entre las placas, el campo eléctrico es idéntico al que habría en vacío
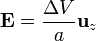
La mayor diferencia de potencial que se puede aplicar será la correspondiente al campo crítico.
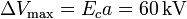
La carga que almacenará el condensador en este valor límite será
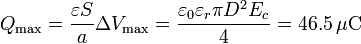
Un aspecto interesante de este resultado es que no depende de la distancia entre las placas.
3 Condensador parcialmente lleno
Cuando tenemos dos capas de aire (de permitividad  ) el problema se complica porque el campo crítico es diferente en cada medio y también lo es el valor del campo que existe en cada región.
) el problema se complica porque el campo crítico es diferente en cada medio y también lo es el valor del campo que existe en cada región.
Operando como en el problema “Condensador con dos capas de dieléctrico”, tenemos tres valores del campo, uniformes en cada región, que verifican
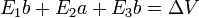
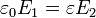
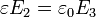
siendo b el espesor de la capa de aire.
Resolviendo este sistema de ecuaciones obtenemos
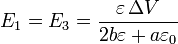
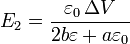
Para una diferencia de potencial dada, el campo es más intenso en la capa de aire (porque  ), donde además el campo de ruptura es menor. Por tanto, la condición para que salte la chispa es que
), donde además el campo de ruptura es menor. Por tanto, la condición para que salte la chispa es que
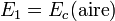

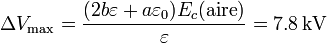
bastante inferior al anterior, pues el campo de ruptura en el aire es 10 veces más pequeño que en el metacrilato.
La capacidad de este condensador es
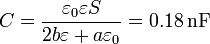
y la carga máxima posible
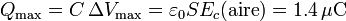
Vemos que en el resultado final no aparece el metacrilato. Esto se entiende observando que el sistema equivale a tres condensadores puestos en serie, y por tanto los tres cargados en la misma magnitud. Cuando salta la chispa lo hace en el que tenga el menor campo critico, que es uno de los dos llenos de aire. Es la carga de este condensador la máxima posible, y por ello no aparece el condensador lleno de metacrilato.
4 Cable coaxial
4.1 Máxima diferencia de potencial
En el caso de un cable coaxial tenemos que el campo no tiene el mismo valor en todos los puntos, ya que el potencial varía con la posición como en el caso de un condensador coaxial
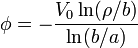
El campo entre los dos cilindros (y por tanto en el dieléctrico) vale
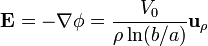
Este campo es más intenso en las proximidades del cilindro interior y más débil junto al cilindro exterior. Para que salte la chispa debe producirse la ruptura en todo el dieléctrico, por lo que la condición la da el que el campo mínimo coincida con el de ruptura.
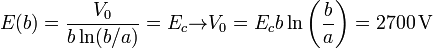
En este apartado, la presencia del dieléctrico es importante, no sólo porque de su naturaleza depende el campo de ruptura, sino porque el comportamiento de un condensador coaxial lleno de aire es diferente del caso relleno de un dieléctrico sólido. En el aire puede producirse el efecto corona en el que la descarga se produce en la región de campo más intenso, junto al hilo central.
4.2 Máxima carga
Una vez que tenemos la máxima diferencia de potencial, la carga almacenada en el condensador es inmediato
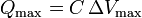
siendo la capacidad de este condensador coaxial
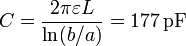
y la carga máxima
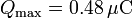
4.3 Máxima energía
De forma similar se halla la energía máxima que almacena el condensador