Rotaciones de un sólido rígido
De Laplace
(→Fórmulas de Poisson) |
|||
| (8 ediciones intermedias no se muestran.) | |||
| Línea 172: | Línea 172: | ||
===Fórmulas de Poisson=== | ===Fórmulas de Poisson=== | ||
| - | Consideremos una rotación instantánea alrededor del eje OZ. En este caso, el extremo del vector | + | Consideremos una rotación instantánea alrededor del eje OZ. En este caso, el extremo del vector <math>\vec{\imath}_2</math> describe un arco de circunferencia en torno al origen. Su velocidad instantánea, por tanto es la correspondiente a un movimiento circular con una cierta velocidad angular |
<center><math>\frac{\mathrm{d}\vec{\imath}_2}{\mathrm{d}t}=\vec{\omega}\times\vec{\imath}_2 \qquad\qquad \vec{\omega}=\omega\vec{k}_2=\omega\vec{k}_1</math></center> | <center><math>\frac{\mathrm{d}\vec{\imath}_2}{\mathrm{d}t}=\vec{\omega}\times\vec{\imath}_2 \qquad\qquad \vec{\omega}=\omega\vec{k}_2=\omega\vec{k}_1</math></center> | ||
| Línea 189: | Línea 189: | ||
<center><math>\frac{\mathrm{d}\vec{\imath}_2}{\mathrm{d}t}=\vec{\omega}\times\vec{\imath}_2 \qquad\qquad \frac{\mathrm{d}\vec{\jmath}_2}{\mathrm{d}t}=\vec{\omega}\times\vec{\jmath}_2 | <center><math>\frac{\mathrm{d}\vec{\imath}_2}{\mathrm{d}t}=\vec{\omega}\times\vec{\imath}_2 \qquad\qquad \frac{\mathrm{d}\vec{\jmath}_2}{\mathrm{d}t}=\vec{\omega}\times\vec{\jmath}_2 | ||
\qquad\qquad \frac{\mathrm{d}\vec{k}_2}{\mathrm{d}t}=\vec{\omega}\times\vec{k}_2</math></center> | \qquad\qquad \frac{\mathrm{d}\vec{k}_2}{\mathrm{d}t}=\vec{\omega}\times\vec{k}_2</math></center> | ||
| - | Estas son las conocidas como fórmulas de Poisson. Aquí | + | Estas son las conocidas como fórmulas de Poisson. Aquí <math>\vec{\omega}</math> es un cierto vector en la dirección del eje de rotación que mide la velocidad angular con la que el sólido gira en dicho instante alrededor del eje. |
| - | <center>[[Archivo:Rotación-instantanea-base.png| | + | <center>[[Archivo:Rotación-instantanea-base.png|500px]]</center> |
Llevando esto a la velocidad instantánea de cada punto obtenemos el campo de velocidades | Llevando esto a la velocidad instantánea de cada punto obtenemos el campo de velocidades | ||
| Línea 208: | Línea 208: | ||
;Hay un eje instantáneo de rotación: Todos los puntos de la recta que pasa por O y lleva la dirección de la velocidad angular poseen velocidad nula | ;Hay un eje instantáneo de rotación: Todos los puntos de la recta que pasa por O y lleva la dirección de la velocidad angular poseen velocidad nula | ||
| - | <center><math>\overrightarrow{OP}=\lambda \vec{\omega}\qquad\ | + | <center><math>\overrightarrow{OP}=\lambda \vec{\omega}\qquad\Rightarrow\qquad \vec{v}_P=\vec{0}</math></center> |
;Misma estructura en planos paralelos: Sean A y B dos puntos del espacio tales que su posición relativa es paralela a <math>\vec{\omega}</math>, esto es, se hallan sobre una recta paralela al eje instantáneo de rotación. Entonces se cumple que sus velocidades son iguales | ;Misma estructura en planos paralelos: Sean A y B dos puntos del espacio tales que su posición relativa es paralela a <math>\vec{\omega}</math>, esto es, se hallan sobre una recta paralela al eje instantáneo de rotación. Entonces se cumple que sus velocidades son iguales | ||
| Línea 215: | Línea 215: | ||
:esto quiere decir que podemos reducir el estudio a la distribución sobre un plano perpendicular al eje de rotación. En los planos paralelos a éste la distribución será idéntica. | :esto quiere decir que podemos reducir el estudio a la distribución sobre un plano perpendicular al eje de rotación. En los planos paralelos a éste la distribución será idéntica. | ||
| - | ;La velocidad de cada punto está contenida en un plano normal al eje y cumple la regla de la mano derecha: Sea | + | ;La velocidad de cada punto está contenida en un plano normal al eje y cumple la regla de la mano derecha: Sea P un punto del plano perpendicular al eje y que pasa por O. En ese caso, al ser la velocidad <math>\vec{v}_P=\vec{\omega}\times \overrightarrow{OP}</math>, es perpendicular al eje y por tanto está contenida en el plano. Además, al tratarse de un producto vectorial, lleva una dirección y sentido perpendicular al vector radial <math>\overrightarrow{OP}</math>, es decir, es tangente a una circunferencia con centro O y con sentido el de la regla de la mano derecha. |
| + | ;La rapidez es proporcional a la distancia al eje: Considerando P un punto del plano anterior se cumple | ||
| + | |||
| + | <center><math>|\vec{v}|=|\vec{\omega}\times\overrightarrow{OP}|=|\vec{\omega}||\overrightarrow{OP}|=|\vec{\omega}|d</math></center> | ||
| + | |||
| + | :por tanto, cuanto más lejos del eje, mayor es la rapidez de cada punto. | ||
| + | |||
| + | <center>[[Archivo:Rotacion-pura.png]]{{qquad}}{{qquad}}[[Archivo:Rotacion-pura-cenital.png]]</center> | ||
| + | |||
==Rotaciones permanentes== | ==Rotaciones permanentes== | ||
| + | Un sólido estará en rotación permanente cuando su movimiento instantáneo en todo momento es uno de rotación. Sin embargo, dado que el eje instantáneo de rotación puede ser diferente en cada instante, en general no habrá ningún punto fijo del sólido y el movimiento sobre un intervalo puede ser muy complejo. | ||
| + | |||
| + | Dentro de las rotaciones permanentes hay dos casos particulares destacados: cuando uno de los puntos del sólido es siempre fijo, y cuando es el eje completo el fijo. | ||
===Sólido con un punto fijo=== | ===Sólido con un punto fijo=== | ||
| + | Supongamos el caso particular | ||
| + | <center><math>\vec{v}_O=\vec{0}\qquad\qquad \forall t</math></center> | ||
| + | En este caso tenemos un punto O para el cual la velocidad es siempre nula y, por tanto, se encuentra permanentemente en reposo. Esto ocurre, por ejemplo, en el caso de una peonza apoyada en su extremo, o en un sólido libre cuyo centro de masas permanece estacionario. | ||
| + | |||
| + | <center>[[Archivo:precesion-giroscopo.gif]]</center> | ||
| + | |||
| + | El movimiento del sólido es, en cada instante, una rotación en torno a un eje que pasa por este punto. | ||
| + | No podemos asegurar que haya más puntos permanentemente en reposo, ya que la orientación del eje de giro puede cambiar con el tiempo haciendo que los puntos instantáneamente en reposo sean diferentes en cada momento. La trayectoria de cada punto individual puede ser extremadamente complicada. NO describen una circunferencia. | ||
| + | |||
| + | El movimiento de un sólido con un punto fijo se puede descomponer como una superposición de tres movimientos distintos: | ||
| + | ;Rotación propia: movimiento alrededor del eje instantáneo de rotación. | ||
| + | ;Precesión: Giro del eje de instantáneo de rotación alrededor de un eje fijo. | ||
| + | ;Nutación: variación del ángulo que el eje instantáneo de rotación forma cn el mismo eje fijo. | ||
| + | |||
| + | <center>[[Archivo:Nutacion.png|400px]]</center> | ||
===Sólido con un eje fijo=== | ===Sólido con un eje fijo=== | ||
| + | Supongamos el caso aún más restrictivo | ||
| + | |||
| + | <center><math>\vec{v}_O=\vec{0}\qquad\qquad\vec{v}_A=\vec{0}\qquad\qquad \forall t</math></center> | ||
| + | es decir, el sólido tiene dos puntos fijos. En este caso, el sólido efectúa en todo momento una rotación con eje el que pasa por O y A. La velocidad angular (que puede depender del tiempo) irá siempre en la dirección de este eje | ||
| + | |||
| + | <center><math>\vec{\omega}\parallel\overrightarrow{OA} \qquad\qquad \vec{\omega}=\omega\vec{u}_{OA}=\omega\frac{\overrightarrow{OA}}{|\overrightarrow{OA}|}</math></center> | ||
| + | |||
| + | Se dice que el sólido es un ''rotor''. Este es un elemento típico de máquinas y mecanismos, en que un eje es sujeto por dos puntos y el sólido obligado a girar en torno a él. Para este caso, sí es cierto que la trayectoria de los diferentes puntos es una circunferencia (o un arco de circunferencia). | ||
| + | |||
| + | Un ejemplo es el de un péndulo cuya barra es rígida y por tanto de longitud constante. La lenteja del péndulo efectúa un movimiento que, aunque oscilante, es de rotación en torno a un eje fijo. | ||
| + | |||
[[Categoría:Cinemática del sólido rígido (CMR)]] | [[Categoría:Cinemática del sólido rígido (CMR)]] | ||
última version al 11:25 14 nov 2023
Contenido |
1 Concepto de rotación
Un sólido rígido experimenta una rotación cuando como resultado del movimiento uno de sus puntos mantiene su posición invariante
2 Rotaciones finitas
2.1 Expresión de las rotaciones
Supongamos que en una rotación el punto fijo es O, que tomaremos como origen de coordenadas. En una rotación, cualquier punto pasará de la posición
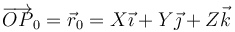
a la posición
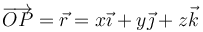
Deseamos establecer la relación entre estos dos vectores.
Para ello, emplearemos dos sistemas de referencia. El sistema fijo “1” es el que consideramos inmóvil y respecto al cual se mueve el sólido. Los dos vectores que acabamos de escribir estarían expresados en la base 1. El sistema ligado “2” es uno móvil que gira solidariamente con el cuerpo en todo momento (es decir, es equivalente a él).
En ese caso, al estar ligado al sólido, la posición de los puntos de éste son constantes en todo momento. Es decir, la posición de P
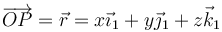
con x, y, z funciones del tiempo se expresará en la base 2
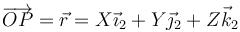
con X, Y y Z constantes (pero 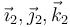 funciones del tiempo). Nótese que en ambos casos se trata del mismo vector, expresado en dos bases distintas.
funciones del tiempo). Nótese que en ambos casos se trata del mismo vector, expresado en dos bases distintas.
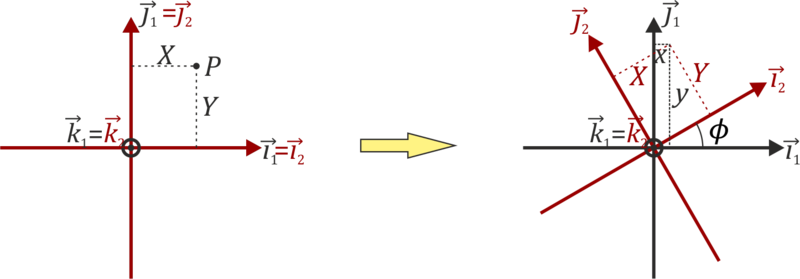
2.1.1 Rotación en torno a OZ
En el caso simple de una rotación de un ángulo θ en torno al eje OZ la relación entre ambas bases es
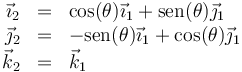
Si llevamos esto a las dos expresiones del vector de posición queda
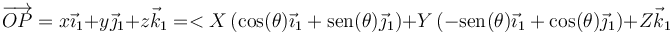
que podemos escribir en la forma matricial
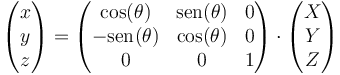
Este es un caso particular de matriz de rotación. Si tenemos en cuenta que (X,Y,Z) son también las coordenadas de la posición inicial en el sistema fijo, podemos decir que el paso de la posición inicial a la final se hace mediante la matriz de rotación.
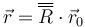
En esta matriz, las columnas representan las componentes de los vectores de la base ligada respecto a la base fija
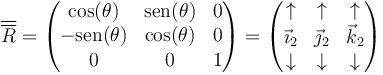
La rotación inversa es la que devuelve a los ejes a la posición original. Esto se consigue mediante una rotación de −θ, con matriz
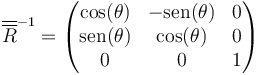
Esta es la traspuesta de la anterior, por lo que en este caso se cumple
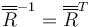
Al mismo tiempo, la rotación inversa es la que pasa del sistema fijo al ligado, por lo que llegamos a que la matriz de rotación tiene por filas las componentes de la base fija en la base ligada
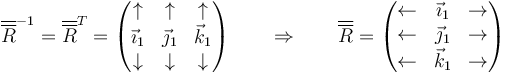
2.1.2 Rotación respecto a un eje arbitrario
El mismo principio se aplica a una rotación en torno a cualquier otro eje.
Inicialmente, el sistema fijo y el ligado son coincidentes. Cada punto tiene las mismas coordenadas en ambos sistemas de referencia
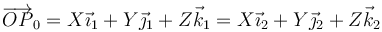
Tras la rotación, la base ligada tendrá unas ciertas componentes respecto a la fija
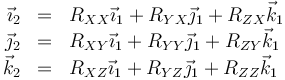
Estas componentes representan la proyección de una base sobre la otra. Por tratarse de vectores unitarios son iguales a su vez a los cosenos de los ángulos que forman. Así

La posición de un punto del sólido permanece constante en la base ligada
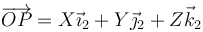
Para hallar las componentes en la base 1 proyectamos sobre cada vector de esta base
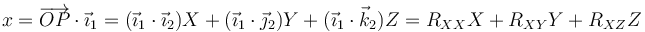
y análogamente para las otras dos componentes. Podemos escribir este resultado en forma matricial
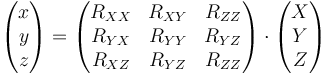
que podemos abreviar como
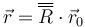
donde 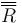 es la matriz de rotación que relaciona las componentes iniciales del vector de posición (o las que tiene en una base ligada al sólido) con las que tiene en un instante posterior. Esta matriz será función del tiempo.
es la matriz de rotación que relaciona las componentes iniciales del vector de posición (o las que tiene en una base ligada al sólido) con las que tiene en un instante posterior. Esta matriz será función del tiempo.
Asmismo, cada fila corresponde a las componentes de un vector de la base fija (1) expresado en la base ligada al sólido (2), y cada columna un vector de la base ligada al sólido expresado en la base fija. Simbólicamente
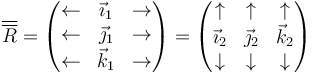
2.1.3 Propiedades de la matriz de rotación
- Tiene tres grados de libertad
- De acuerdo con la expresión anterior, parece que para expresar una rotación hay que proporcionar 9 parámetros, esto es, que tiene 9 grados de libertad. No es así, ya que tenemos seis vínculos entre las componentes. Por ser ortonormal cada base
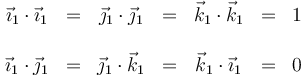
- Estos seis vínculos reducen el número de grados de libertad a 3, que pueden ser tres ángulos de orientación, como los ángulos de Euler.
- Es ortogonal
- Una matriz es ortogonal cuando su traspuesta coincide con su inversa. Si una rotación dada lleva de la base 1 a la base 2, la rotación inversa será la que devuelve la base 2 a la base 1. Por la construcción de la matriz, el intercambiar 1 por 2 equivale a intercambiar filas por columnas, esto es, hallar la traspuesta. Por tanto

- (empleamos
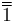 en vez de
en vez de 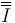 , para reservar esta letra para los momentos de inercia) Esta propiedad equivale a lo que hemos mencionado de que las dos bases 1 y 2 son bases ortonormales.
, para reservar esta letra para los momentos de inercia) Esta propiedad equivale a lo que hemos mencionado de que las dos bases 1 y 2 son bases ortonormales.
- Es unitaria
- Una matriz es unitaria si su determinante vale la unidad. Es consecuencia inmediata de lo anterior
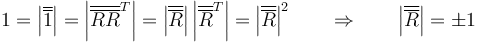
- La raíz negativa la descartamos, ya que corresponde a las simetrías, que hemos considerado como imposibles en el movimiento de un sólido real.
3 Teorema de Euler. Eje de rotación
Hemos definido como un movimiento rígido que deja un punto fijo. Euler demostró que esto implica que no hay un solo punto fijo, sino toda una recta que pasa por O. Esta recta es el llamado eje de rotación.
La demostración se basa en que debe haber un vector no afectado por la rotación, esto es,
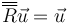
Si este vector  existe, cualquier múltiplo de él tampoco se verá afectado, con lo que obtenemos toda una recta que pasa por O.
existe, cualquier múltiplo de él tampoco se verá afectado, con lo que obtenemos toda una recta que pasa por O.
En términos algebraicos esto equivale a decir que existe un autovalor unidad, siendo  el autovector correspondiente. La condición para que ello ocurra es que
el autovector correspondiente. La condición para que ello ocurra es que
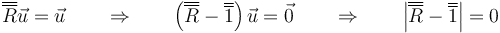
Veamos que es cierto:
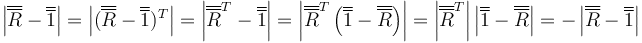
y por tanto

Por tanto existe el autovalor unidad, y el autovector correspondiente nos da el eje de rotación.
Esto nos da otra forma de parametricar las rotaciones: con dos ángulos (por ejemplo los de las coordenadas esféricas) damos la orientación de este vector director y con un tercer ángulo medimos cuánto ha girado el sólido en torno al eje.
Como consecuencia del teorema de Euler, cualquier vector perpendicular al eje de giro sigue siendo perpendicular tras la rotación. Si el vector 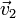 se transforma en el
se transforma en el 
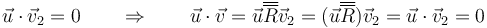
Cualquier otro vector podrá descomponerse en una parte paralela al eje de giro (que no se verá afectada por la rotación) más una parte ortogonal al eje (que gira un cierto ángulo en torno al eje, manteniéndose ortogonal).
4 Rotaciones instantáneas
El apartado anterior se refiere a rotaciones finitas, que relacionan lo que ocurre en un instante con otro un cierto intervalo más tarde. Cuando este intervalo es infinitesimal tenemos una rotación instantánea. En una rotación instantánea tendremos un eje instantáneo de rotación y el ángulo girado será un dθ.
La velocidad de los puntos de un sólido en rotación instantánea no será la misma para todos. En concreto, los puntos del eje de rotación se encuentran en reposo en ese instante. Por ello, en este se denomina eje instantáneo de rotación (EIR), ya que su dirección puede estar cambiando con el tiempo.
La velocidad de cada punto la podemos calcular con ayuda de la base ligada, ya que al ser constantes las componentes de la posición
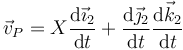
Por tanto, solo precisamos conocer la derivada de los vectores de la base.
4.1 Fórmulas de Poisson
Consideremos una rotación instantánea alrededor del eje OZ. En este caso, el extremo del vector 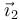 describe un arco de circunferencia en torno al origen. Su velocidad instantánea, por tanto es la correspondiente a un movimiento circular con una cierta velocidad angular
describe un arco de circunferencia en torno al origen. Su velocidad instantánea, por tanto es la correspondiente a un movimiento circular con una cierta velocidad angular

y lo mismo ocurre con el 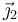 mientras que el
mientras que el 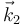 permanece constante.
permanece constante.
Supongamos ahora el giro alrededor de un eje arbitrario, oreientado según el vector  , de tal manera que
, de tal manera que
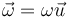
Podemos descomponer el vector 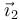 en una parte paralela a
en una parte paralela a  y una ortogonal a él. La parte paralela no se ve afectada por la rotación, mientras que la perpendicular efectúa un arco diferencial de circunferencia
y una ortogonal a él. La parte paralela no se ve afectada por la rotación, mientras que la perpendicular efectúa un arco diferencial de circunferencia
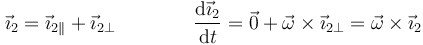
donde la última identidad se cumple porque 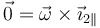 . La misma relación se verifica para los otros dos vectores de la base
. La misma relación se verifica para los otros dos vectores de la base
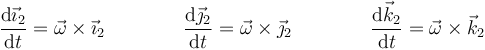
Estas son las conocidas como fórmulas de Poisson. Aquí  es un cierto vector en la dirección del eje de rotación que mide la velocidad angular con la que el sólido gira en dicho instante alrededor del eje.
es un cierto vector en la dirección del eje de rotación que mide la velocidad angular con la que el sólido gira en dicho instante alrededor del eje.
| Error al crear miniatura: |
Llevando esto a la velocidad instantánea de cada punto obtenemos el campo de velocidades
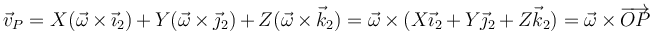
Esta fórmula también es conocida como de Poisson y nos da el campo de velocidades instantáneas para el sólido en rotación instantánea.
5 Campo de velocidades
Según la fórmula de Poisson, el campo de velocidades de un sólido rígido que se encuentra instantáneamente en rotación alrededor del punto fijo O tiene la expresión
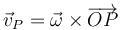
siendo  la velocidad angular instantánea del sólido. Este campo de velocidades posee una serie de propiedades características:
la velocidad angular instantánea del sólido. Este campo de velocidades posee una serie de propiedades características:
- Hay un eje instantáneo de rotación
- Todos los puntos de la recta que pasa por O y lleva la dirección de la velocidad angular poseen velocidad nula
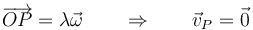
- Misma estructura en planos paralelos
- Sean A y B dos puntos del espacio tales que su posición relativa es paralela a
 , esto es, se hallan sobre una recta paralela al eje instantáneo de rotación. Entonces se cumple que sus velocidades son iguales
, esto es, se hallan sobre una recta paralela al eje instantáneo de rotación. Entonces se cumple que sus velocidades son iguales
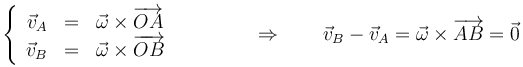
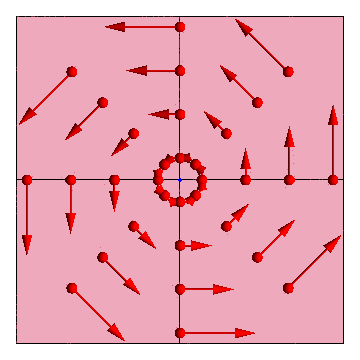
- esto quiere decir que podemos reducir el estudio a la distribución sobre un plano perpendicular al eje de rotación. En los planos paralelos a éste la distribución será idéntica.
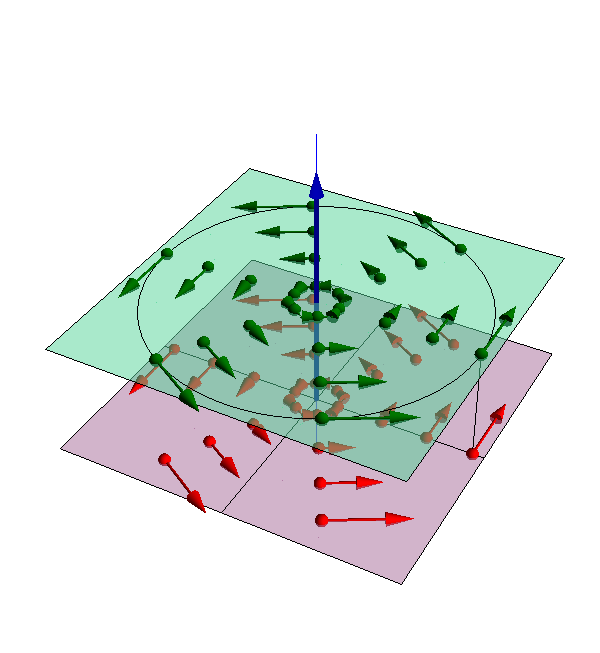
- La velocidad de cada punto está contenida en un plano normal al eje y cumple la regla de la mano derecha
- Sea P un punto del plano perpendicular al eje y que pasa por O. En ese caso, al ser la velocidad
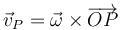 , es perpendicular al eje y por tanto está contenida en el plano. Además, al tratarse de un producto vectorial, lleva una dirección y sentido perpendicular al vector radial
, es perpendicular al eje y por tanto está contenida en el plano. Además, al tratarse de un producto vectorial, lleva una dirección y sentido perpendicular al vector radial  , es decir, es tangente a una circunferencia con centro O y con sentido el de la regla de la mano derecha.
, es decir, es tangente a una circunferencia con centro O y con sentido el de la regla de la mano derecha.
- La rapidez es proporcional a la distancia al eje
- Considerando P un punto del plano anterior se cumple
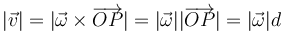
- por tanto, cuanto más lejos del eje, mayor es la rapidez de cada punto.
6 Rotaciones permanentes
Un sólido estará en rotación permanente cuando su movimiento instantáneo en todo momento es uno de rotación. Sin embargo, dado que el eje instantáneo de rotación puede ser diferente en cada instante, en general no habrá ningún punto fijo del sólido y el movimiento sobre un intervalo puede ser muy complejo.
Dentro de las rotaciones permanentes hay dos casos particulares destacados: cuando uno de los puntos del sólido es siempre fijo, y cuando es el eje completo el fijo.
6.1 Sólido con un punto fijo
Supongamos el caso particular

En este caso tenemos un punto O para el cual la velocidad es siempre nula y, por tanto, se encuentra permanentemente en reposo. Esto ocurre, por ejemplo, en el caso de una peonza apoyada en su extremo, o en un sólido libre cuyo centro de masas permanece estacionario.

El movimiento del sólido es, en cada instante, una rotación en torno a un eje que pasa por este punto. No podemos asegurar que haya más puntos permanentemente en reposo, ya que la orientación del eje de giro puede cambiar con el tiempo haciendo que los puntos instantáneamente en reposo sean diferentes en cada momento. La trayectoria de cada punto individual puede ser extremadamente complicada. NO describen una circunferencia.
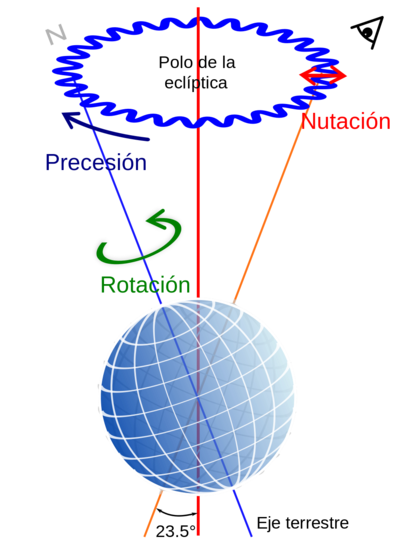
El movimiento de un sólido con un punto fijo se puede descomponer como una superposición de tres movimientos distintos:
- Rotación propia
- movimiento alrededor del eje instantáneo de rotación.
- Precesión
- Giro del eje de instantáneo de rotación alrededor de un eje fijo.
- Nutación
- variación del ángulo que el eje instantáneo de rotación forma cn el mismo eje fijo.
6.2 Sólido con un eje fijo
Supongamos el caso aún más restrictivo
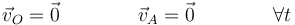
es decir, el sólido tiene dos puntos fijos. En este caso, el sólido efectúa en todo momento una rotación con eje el que pasa por O y A. La velocidad angular (que puede depender del tiempo) irá siempre en la dirección de este eje
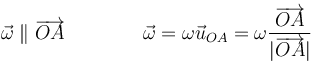
Se dice que el sólido es un rotor. Este es un elemento típico de máquinas y mecanismos, en que un eje es sujeto por dos puntos y el sólido obligado a girar en torno a él. Para este caso, sí es cierto que la trayectoria de los diferentes puntos es una circunferencia (o un arco de circunferencia).
Un ejemplo es el de un péndulo cuya barra es rígida y por tanto de longitud constante. La lenteja del péndulo efectúa un movimiento que, aunque oscilante, es de rotación en torno a un eje fijo.





