Movimiento plano de una partícula (CMR)
De Laplace
(→Resumen de expresiones) |
(→Coordenadas polares) |
||
| (6 ediciones intermedias no se muestran.) | |||
| Línea 22: | Línea 22: | ||
==Coordenadas polares== | ==Coordenadas polares== | ||
| - | En el caso de movimiento en un plano, es útil considerar las coordenadas polares para describir el movimiento de la partícula, <math>\{\rho,\ | + | En el caso de movimiento en un plano, es útil considerar las coordenadas polares para describir el movimiento de la partícula, <math>\{\rho,\theta\}</math>. Estas coordenadas son la distancia al origen del sistema de referencia <math>(\rho)</math> y el ángulo que forma el vector de posición con el eje <math>OX</math> <math>(\theta)</math>. |
| - | <center><math>x = \rho\cos(\ | + | <center><math>x = \rho\cos(\theta) \qquad y = |
| - | \rho\,\mathrm{sen}(\ | + | \rho\,\mathrm{sen}(\theta)</math></center> |
y sus inversas | y sus inversas | ||
<center><math>\rho = \sqrt{x^2+y^2}\qquad | <center><math>\rho = \sqrt{x^2+y^2}\qquad | ||
| - | \ | + | \theta=\mathrm{arctg}\left(\frac{y}{x}\right)</math></center> |
| - | Las coordenadas polares llevan asociadas una base vectorial <math>\{\vec{u}_{\rho},\vec{u}_{\ | + | Las coordenadas polares llevan asociadas una base vectorial <math>\{\vec{u}_{\rho},\vec{u}_{\theta}\}</math>, que apuntan respectivamente en la dirección radial (en la que varía <math>\rho</math>) y acimutal (en la que varía <math>\theta</math>). Esta base se relaciona con la canónica por el cambio de base |
<center><math>\begin{array}{rcl} | <center><math>\begin{array}{rcl} | ||
| - | \vec{u}_\rho & = & \cos(\ | + | \vec{u}_\rho & = & \cos(\theta)\vec{\imath}+\mathrm{sen}(\theta)\vec{\jmath} \\ |
| - | \vec{u}_\ | + | \vec{u}_\theta & = & -\mathrm{sen}(\theta)\vec{\imath}+\cos(\theta)\vec{\jmath} |
| - | \end{array}</math>{{qquad}}ó{{qquad}}<math>\begin{pmatrix}\vec{u}_\rho \\\vec{u}_\ | + | \end{array}</math>{{qquad}}ó{{qquad}}<math>\begin{pmatrix}\vec{u}_\rho \\\vec{u}_\theta\end{pmatrix} = \begin{pmatrix}\cos(\theta) & \mathrm{sen}(\theta)\\ -\mathrm{sen}(\theta) & \cos(\theta)\end{pmatrix}\cdot \begin{pmatrix}\vec{\imath} \\\vec{\jmath}\end{pmatrix}</math> </center> |
y su inverso | y su inverso | ||
<center><math>\begin{array}{rcl} | <center><math>\begin{array}{rcl} | ||
| - | \vec{\imath} & = & \cos(\ | + | \vec{\imath} & = & \cos(\theta)\vec{u}_\rho-\mathrm{sen}(\theta)\vec{u}_\theta \\ |
| - | \vec{\jmath} & = & \mathrm{sen}(\ | + | \vec{\jmath} & = & \mathrm{sen}(\theta)\vec{u}_\rho+\cos(\theta)\vec{u}_\theta |
| - | \end{array}</math>{{qquad}}ó{{qquad}}<math>\begin{pmatrix}\vec{\imath} \\\vec{\jmath}\end{pmatrix} = \begin{pmatrix}\cos(\ | + | \end{array}</math>{{qquad}}ó{{qquad}}<math>\begin{pmatrix}\vec{\imath} \\\vec{\jmath}\end{pmatrix} = \begin{pmatrix}\cos(\theta) & -\mathrm{sen}(\theta)\\ \mathrm{sen}(\theta) & \cos(\theta)\end{pmatrix}\cdot \begin{pmatrix}\vec{u}_\rho \\\vec{u}_\theta\end{pmatrix}</math> </center> |
| - | <center>[[Archivo:vectores-polares.png]]{{qquad}}{{qquad}}[[Archivo:cartesianas-polares.png]]</center> | + | <center>[[Archivo:vectores-polares.png|400px]]{{qquad}}{{qquad}}[[Archivo:cartesianas-polares.png|369px]]</center> |
Los vectores unitarios en polares dependen de la posición. Aunque tengan el mismo nombre, el vector <math>\vec{u}_\rho</math> en un punto es diferente del vector <math>\vec{u}_\rho</math> en otro. Por ello, hay que tener un cuidado infinito a la hora de operar con vectores en coordenadas polares. | Los vectores unitarios en polares dependen de la posición. Aunque tengan el mismo nombre, el vector <math>\vec{u}_\rho</math> en un punto es diferente del vector <math>\vec{u}_\rho</math> en otro. Por ello, hay que tener un cuidado infinito a la hora de operar con vectores en coordenadas polares. | ||
| Línea 55: | Línea 55: | ||
En particular, cuando consideramos el movimiento de una partícula, su posición, y por tanto los vectores de la base en polares, son funciones del tiempo. Por ello, cuando aparezca una derivada o una integral, habrá que tenerlos en cuenta. Sus derivadas respecto del tiempo valen | En particular, cuando consideramos el movimiento de una partícula, su posición, y por tanto los vectores de la base en polares, son funciones del tiempo. Por ello, cuando aparezca una derivada o una integral, habrá que tenerlos en cuenta. Sus derivadas respecto del tiempo valen | ||
| - | <center><math>\frac{\mathrm{d}\vec{u}_\rho}{\mathrm{d}t}=-\dot{\ | + | <center><math>\frac{\mathrm{d}\vec{u}_\rho}{\mathrm{d}t}=-\dot{\theta}\,\mathrm{sen}(\theta)\vec{\imath}\,+\,\dot{\theta}\cos(\theta)\vec{\jmath}=\dot{\theta}\vec{u}_\theta\qquad |
| - | \frac{\mathrm{d}\vec{u}_\ | + | \frac{\mathrm{d}\vec{u}_\theta}{\mathrm{d}t}=-\dot{\theta}\cos(\theta)\vec{\imath}\,-\,\dot{\theta}\,\mathrm{sen}(\theta)\vec{\jmath}=-\dot{\theta}\vec{u}_\rho</math></center> |
===Posición en polares=== | ===Posición en polares=== | ||
Puesto que el vector <math>\vec{u}_\rho</math> es el unitario en la dirección del vector de posición en el plano tenemos que la expresión de este en polares es | Puesto que el vector <math>\vec{u}_\rho</math> es el unitario en la dirección del vector de posición en el plano tenemos que la expresión de este en polares es | ||
| Línea 65: | Línea 65: | ||
la velocidad la calculamos derivando esta expresión respecto al tiempo, donde debemos recordar que también hay que derivar el vector unitario. Aplicamos la derivada de un producto | la velocidad la calculamos derivando esta expresión respecto al tiempo, donde debemos recordar que también hay que derivar el vector unitario. Aplicamos la derivada de un producto | ||
| - | <center><math>\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t} = \frac{\mathrm{d}\rho}{\mathrm{d}t}\vec{u}_\rho + \rho\frac{\mathrm{d}\vec{u}_\rho}{\mathrm{d}t} = \dot{\rho}\vec{u}_\rho+\rho\dot{\ | + | <center><math>\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t} = \frac{\mathrm{d}\rho}{\mathrm{d}t}\vec{u}_\rho + \rho\frac{\mathrm{d}\vec{u}_\rho}{\mathrm{d}t} = \dot{\rho}\vec{u}_\rho+\rho\dot{\theta}\vec{u}_\theta</math></center> |
Esta expresión nos dice que la velocidad se compone de dos partes, una radial, debida a que la partícula se acerca o aleja del origen de coordenadas, y una acimutal, asociada al giro en torno a éste. | Esta expresión nos dice que la velocidad se compone de dos partes, una radial, debida a que la partícula se acerca o aleja del origen de coordenadas, y una acimutal, asociada al giro en torno a éste. | ||
| Línea 71: | Línea 71: | ||
Por ejemplo, si consideramos una partícula describiendo un movimiento circular alrededor del origen, | Por ejemplo, si consideramos una partícula describiendo un movimiento circular alrededor del origen, | ||
| - | <center><math>\rho = A = \mathrm{cte}\qquad\Rightarrow\qquad \dot{\rho}=0\qquad\qquad \dot{\ | + | <center><math>\rho = A = \mathrm{cte}\qquad\Rightarrow\qquad \dot{\rho}=0\qquad\qquad \dot{\theta}=\omega</math></center> |
y resulta la velocidad | y resulta la velocidad | ||
| - | <center><math>\vec{v} = \overbrace{\dot{\rho}}^{0}\vec{u}_\rho + \overbrace{\rho}^{A}\overbrace{\dot{\ | + | <center><math>\vec{v} = \overbrace{\dot{\rho}}^{0}\vec{u}_\rho + \overbrace{\rho}^{A}\overbrace{\dot{\theta}}^{\omega}\vec{u}_\theta = \omega A\vec{u}_\theta</math></center> |
En un movimiento circular alrededor del origen la velocidad es puramente acimutal, ya que la partícula solo gira en torno al origen. | En un movimiento circular alrededor del origen la velocidad es puramente acimutal, ya que la partícula solo gira en torno al origen. | ||
| Línea 89: | Línea 89: | ||
La expresión de este movimiento en polares es | La expresión de este movimiento en polares es | ||
| - | <center><math>\rho = \sqrt{x^2+y^2} = \sqrt{L^2+v_0^2t^2}\qquad\qquad\ | + | <center><math>\rho = \sqrt{x^2+y^2} = \sqrt{L^2+v_0^2t^2}\qquad\qquad\theta=\,\mathrm{arctg}\left(\frac{y}{x}\right)=\,\mathrm{arctg}\left(\frac{v_0t}{L}\right)</math></center> |
Las derivadas respecto al tiempo de estas dos magnitudes valen | Las derivadas respecto al tiempo de estas dos magnitudes valen | ||
| - | <center><math>\dot{\rho}=\frac{v_0^2 t}{\sqrt{L^2+v_0^2 t^2}}\qquad \dot{\ | + | <center><math>\dot{\rho}=\frac{v_0^2 t}{\sqrt{L^2+v_0^2 t^2}}\qquad \dot{\theta} = \frac{v_0L t}{L^2+v_0^2t^2}</math></center> |
y esto nos da la velocidad instantánea | y esto nos da la velocidad instantánea | ||
| - | <center><math>\vec{v}=\frac{v_0^2 t\vec{u}_\rho+v_0Lt\vec{u}_\ | + | <center><math>\vec{v}=\frac{v_0^2 t\vec{u}_\rho+v_0Lt\vec{u}_\theta}{\sqrt{L^2+v_0^2t^2}}</math></center> |
vemos que aunque el movimiento sea rectilíneo y uniforme, resulta una velocidad radial y una acimutal no nula. Para interpretarlo nos imaginamos a un observador situado en el origen de coordenadas, que apunte en todo momento a la partícula. Este observador ve a la partícula acercarse y alejarse (pasando por un mínimo justo cuando está en la perpendicular a la recta), y también ve cambiar la dirección de observación, lo que equivale a un giro. | vemos que aunque el movimiento sea rectilíneo y uniforme, resulta una velocidad radial y una acimutal no nula. Para interpretarlo nos imaginamos a un observador situado en el origen de coordenadas, que apunte en todo momento a la partícula. Este observador ve a la partícula acercarse y alejarse (pasando por un mínimo justo cuando está en la perpendicular a la recta), y también ve cambiar la dirección de observación, lo que equivale a un giro. | ||
| Línea 104: | Línea 104: | ||
===Aceleración en polares=== | ===Aceleración en polares=== | ||
| - | Operando igualmente obtenemos la expresión de la aceleración en polares, solo que esta vez debemos derivar más términos y también el vector <math>\vec{u}_\ | + | Operando igualmente obtenemos la expresión de la aceleración en polares, solo que esta vez debemos derivar más términos y también el vector <math>\vec{u}_\theta</math> |
| - | <center><math>\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=\ddot{\rho}\vec{u}_\rho + \dot{\rho}\frac{\mathrm{d}\vec{u}_\rho}{\mathrm{d}t} +\dot{\rho}\dot{\ | + | <center><math>\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=\ddot{\rho}\vec{u}_\rho + \dot{\rho}\frac{\mathrm{d}\vec{u}_\rho}{\mathrm{d}t} +\dot{\rho}\dot{\theta}\vec{u}_\theta+\rho\ddot{\theta}\vec{u}_\theta+\rho\dot{\theta}\frac{\mathrm{d}\vec{u}_\theta}{\mathrm{d}t}=(\ddot{\rho}-\rho\,\dot{\theta}^2)\,\vec{u}_{\rho} + (2\dot{\rho}\,\dot{\theta}+\rho\ddot{\theta})\,\vec{u}_{\theta}</math></center> |
En el caso del movimiento circular tenemos que, para la coordenada radial | En el caso del movimiento circular tenemos que, para la coordenada radial | ||
| Línea 114: | Línea 114: | ||
y para la acimutal | y para la acimutal | ||
| - | <center><math>\dot{\ | + | <center><math>\dot{\theta}=\omega\qquad\ddot{\theta}=\alpha</math></center> |
lo que nos da la aceleración lineal | lo que nos da la aceleración lineal | ||
| - | <center><math>\vec{a}=-A\omega^2\vec{u}_\rho+A\alpha\vec{u}_\ | + | <center><math>\vec{a}=-A\omega^2\vec{u}_\rho+A\alpha\vec{u}_\theta</math></center> |
En general tendrá tanto componente radial (que en este caso coincide con la aceleración normal) como componente acimutal (que en este caso coincide con la tangencial). | En general tendrá tanto componente radial (que en este caso coincide con la aceleración normal) como componente acimutal (que en este caso coincide con la tangencial). | ||
| Línea 124: | Línea 124: | ||
En el caso del movimiento rectilíneo y uniforme, tras una serie de cálculos bastante laboriosos se llega a que | En el caso del movimiento rectilíneo y uniforme, tras una serie de cálculos bastante laboriosos se llega a que | ||
| - | <center><math>\ddot{\rho}-\rho\,\dot{\ | + | <center><math>\ddot{\rho}-\rho\,\dot{\theta}^2=0\qquad\qquad \rho\ddot{\theta}+2\dot{\rho}\dot{\theta}=0</math></center> |
y por tanto | y por tanto | ||
| - | <center><math>\vec{a}=0\vec{u}_\rho+0\vec{u}_\ | + | <center><math>\vec{a}=0\vec{u}_\rho+0\vec{u}_\theta = \vec{0}</math></center> |
como corresponde a un movimiento rectilíneo y uniforme. | como corresponde a un movimiento rectilíneo y uniforme. | ||
| Línea 137: | Línea 137: | ||
\begin{array}{rcl} | \begin{array}{rcl} | ||
\vec{r} & = & \rho\,\vec{u}_{\rho}\\ | \vec{r} & = & \rho\,\vec{u}_{\rho}\\ | ||
| - | \vec{v} & = & \dot{\rho}\,\vec{u}_{\rho} + \rho\,\dot{\ | + | \vec{v} & = & \dot{\rho}\,\vec{u}_{\rho} + \rho\,\dot{\theta}\,\vec{u}_{\theta}\\ |
| - | \vec{a} & = &(\ddot{\rho}-\rho\,\dot{\ | + | \vec{a} & = &(\ddot{\rho}-\rho\,\dot{\theta}^2)\,\vec{u}_{\rho} + (2\dot{\rho}\,\dot{\theta}+\rho\ddot{\theta})\,\vec{u}_{\theta} |
\end{array} | \end{array} | ||
</math></center> | </math></center> | ||
| Línea 145: | Línea 145: | ||
<center><math>|\vec{v}| = | <center><math>|\vec{v}| = | ||
| - | \sqrt{\dot{\rho}^2+\rho^2\dot{\ | + | \sqrt{\dot{\rho}^2+\rho^2\dot{\theta}^2}</math></center> |
| + | ==Movimiento circular== | ||
| + | Puesto que los sistemas de referencia son arbitrarios, una vez que sabemos que un movimiento es circular, podemos tomar el origen de coordenadas en el centro de la circunferencia y los ejes de forma que la trayectoria esté contenida en el plano XY y con el origen de coordenadas en el centro de la circunferencia. En coordenadas polares, una circunferencia centrada en el origen se escribe simplemente | ||
| + | |||
| + | <center><math>\rho = R\,</math></center> | ||
| + | |||
| + | La ecuación vectorial de la trayectoria se reduce a | ||
| + | |||
| + | <center><math>\vec{r}=R\vec{u}_\rho = R\cos(\varphi)\vec{\imath}+R\,\mathrm{sen}\,(\varphi)\vec{\jmath}</math></center> | ||
| + | |||
| + | siendo la ley horaria | ||
| + | |||
| + | <center><math>\varphi = \varphi(t)\,</math></center> | ||
| + | |||
| + | La velocidad de un movimiento circular es puramente acimutal, | ||
| + | |||
| + | <center><math>\vec{v}=R\dot{\varphi}\vec{u}_\varphi = R\dot{\varphi}\left(-\,\mathrm{sen}\,(\varphi)\vec{\imath}+\cos(\varphi)\vec{\jmath}\right)</math></center> | ||
| + | |||
| + | siendo la rapidez y el vector tangente | ||
| + | |||
| + | <center><math>|\vec{v}| = R|\dot{\varphi}|</math>{{qquad}}{{qquad}}<math>\vec{T}=\pm \vec{u}_\varphi</math></center> | ||
| + | |||
| + | El signo variable depende del sentido de recorrido sobre la circunferencia. Por ejemplo, el movimiento de la lenteja de un péndulo es circular (aunque no complete una circunferencia) pero en su vaivén, el vector tangente unas veces coincide con el unitario en la dirección acimutal y otras es el opuesto. | ||
| + | |||
| + | La distancia medida sobre la curva | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}s}{\mathrm{d}t}= R\frac{\mathrm{d}\varphi}{\mathrm{d}t}</math>{{tose}} <math>s = s_0+R\varphi\,</math></center> | ||
| + | |||
| + | La velocidad angular va en la dirección normal al plano y es tal que al multiplicarla vectorialmente por <math>\vec{r}</math> resulta la velocidad. Esto da | ||
| + | |||
| + | <center><math>\vec{\omega}=\dot{\varphi}\vec{k}</math></center> | ||
| + | |||
| + | La aceleración de la partícula es | ||
| + | |||
| + | <center><math>\vec{a}=-R\dot{\varphi}^2\vec{u}_\rho + R\ddot{\varphi}\vec{u}_\varphi</math></center> | ||
| + | |||
| + | con componentes intrínsecas | ||
| + | |||
| + | <center><math>\vec{a}_t = R\ddot{\varphi}\vec{T}</math>{{qquad}}{{qquad}}<math>\vec{a}_n=R\dot{\varphi}^2\vec{N}</math></center> | ||
| + | |||
| + | con el vector normal | ||
| + | |||
| + | <center><math>\vec{N}=-\vec{u}_\rho=-\frac{\vec{r}}{R}</math></center> | ||
| + | |||
| + | Por último, la aceleración angular viene dada por | ||
| + | |||
| + | <center><math>\vec{\alpha}=\ddot{\varphi}\vec{k}</math></center> | ||
| + | |||
| + | Con estos ejes, un movimiento circular uniforme corresponde a | ||
| + | |||
| + | <center><math>\varphi = \omega t + \varphi_0\,</math></center> | ||
| + | |||
| + | con <math>\omega</math> constante. | ||
==Triedro de Frenet== | ==Triedro de Frenet== | ||
| + | ===Vectores tangente y normal=== | ||
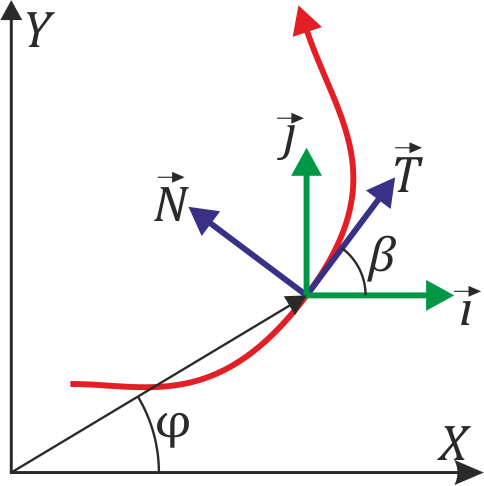
| + | Al estar la velocidad contenida en el plano de movimiento, el vector tangente estará contenido en el mismo plano y formará un cierto ángulo variable θ con el eje OX | ||
| + | |||
| + | <center><math>\vec{T}=\cos(\beta)\vec{\imath}+\mathrm{sen}(\beta)\vec{\jmath}</math></center> | ||
| + | |||
| + | [[Archivo:frenet-plano.png|right]] | ||
| + | |||
| + | Al pasar el tiempo, este ángulo irá cambiando por lo que | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}\vec{T}}{\mathrm{d}t}=\frac{\mathrm{d}\vec{T}}{\mathrm{d}\beta}\,\frac{\mathrm{d}\beta}{\mathrm{d}t}=\left(-\mathrm{sen}(\beta)\vec{\imath}+\cos(\beta)\vec{\jmath}\right)\dot{\beta}</math></center> | ||
| + | |||
| + | El primer factor es un vector unitario y ortogonal a <math>\vec{T}</math>, esto es, se trata del vector normal <math>\vec{N}</math>. | ||
| + | |||
| + | <center><math>\vec{N}=-\mathrm{sen}(\beta)\vec{\imath}+\cos(\beta)\vec{\jmath}</math></center> | ||
| + | |||
| + | Nótese la similtud con la expresión de la base en coordenadas polares, que puede inducir a confusión. En coordenadas polares, <math>\varphi</math> es el ámgulo que el ''vector de posición'' forma con el eje OX. En el triedro intrínseco, <math>\beta</math> es el ángulo que la ''velocidad'' forma con dicho eje. | ||
| + | |||
| + | ===Vector binormal=== | ||
| + | Si multiplicamos vectorialmente el vector tangente y el vector normal obtenemos que el vector binormal es constante, como corresponde a un movimiento plano. | ||
| + | |||
| + | <center><math>\vec{B}=\vec{T}\times\vec{N}=\vec{k}</math></center> | ||
| + | |||
| + | ===Interpretación del radio y el centro de curvatura=== | ||
| + | Si particularizamos para el caso del movimiento plano, es fácil dar un significado geométrico al radio de curvatura. | ||
| + | |||
| + | De la derivada temporal del vector tangente obtenemos | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}\vec{T}}{\mathrm{d}t} = \dot{\beta}\vec{N}</math></center> | ||
| + | |||
| + | pero en un movimiento plano, la rapidez con que varía un ángulo es una velocidad angular, que para un movimiento circular equivale a la velocidad lineal dividida por el radio | ||
| + | |||
| + | <center><math>\dot{\beta}=\omega = \frac{|\vec{v}|}{R}</math></center> | ||
| + | |||
| + | por lo que escribimos | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}\vec{T}}{\mathrm{d}t} = \frac{|\vec{v}|}{R}\vec{N}</math></center> | ||
| + | |||
| + | El radio de curvatura, R, equivale entonces al radio de la circunferencia que, en un instante dado, está describiendo a la partícula, o para ser más precisos, la circunferencia que más se aproxima a la trayectoria en dicho instante (misma posición, misma velocidad y misma aceleración). Esta circunferencia tangente se denomina circunferencia osculatriz. Su centro es el centro de curvatura. | ||
| + | |||
[[Categoría:Mecánica de la partícula y de los sistemas (CMR)]] | [[Categoría:Mecánica de la partícula y de los sistemas (CMR)]] | ||
última version al 18:55 28 oct 2016
Contenido |
1 Introducción
En mecánica, el movimiento plano de un sistema de partículas es aquél en que las velocidades de las diferentes partículas están en todo momento contenidas en planos paralelos (denominnados planos directores) constantes para cada partícula.
2 Posición, velocidad y aceleración
La estructura del movimiento plano nos permite elegir un sistema de ejes en el que el eje OZ es el perpendicular a estos planos, de forma que la posición de cada partícula puede ponerse en la forma
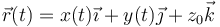
siendo z0 una constante para cada partícula (no necesariamente la misma para todas pues pueden moverse en planos paralelos).
Si nos centramos en una sola partícula, su trayectoria es una curva plana que puede ser representada gráficamente de forma más simple.
En este sistema de referencia la velocidad posee solo dos componentes
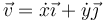
y lo mismo ocurre con la aceleración

Gráficamente, ambos vectores están contenidos en el plano de la trayectoria, siendo la velocidad tangente a ella y la aceleración formando un cierto ángulo pero siempre apuntando hacia el interior de la curva.
3 Coordenadas polares
En el caso de movimiento en un plano, es útil considerar las coordenadas polares para describir el movimiento de la partícula, {ρ,θ}. Estas coordenadas son la distancia al origen del sistema de referencia (ρ) y el ángulo que forma el vector de posición con el eje OX (θ).

y sus inversas

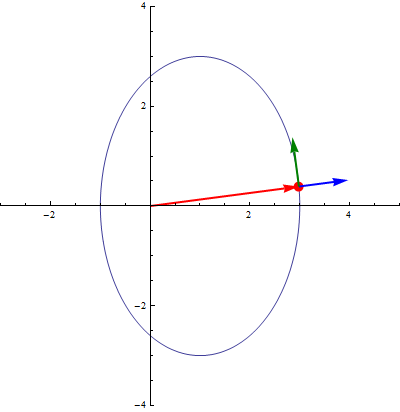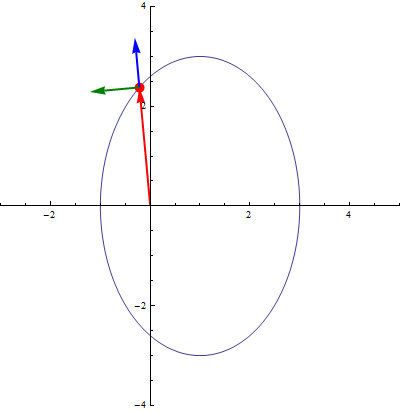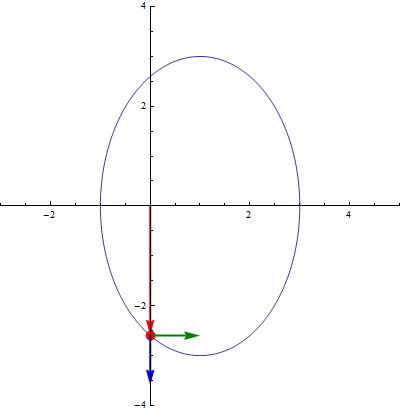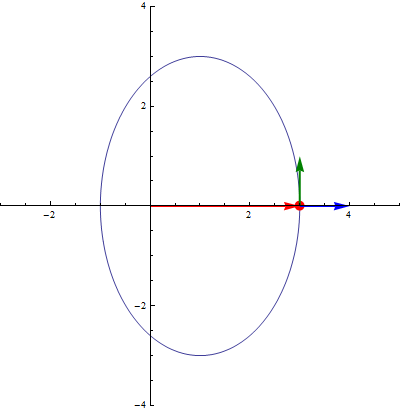
Las coordenadas polares llevan asociadas una base vectorial 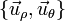 , que apuntan respectivamente en la dirección radial (en la que varía ρ) y acimutal (en la que varía θ). Esta base se relaciona con la canónica por el cambio de base
, que apuntan respectivamente en la dirección radial (en la que varía ρ) y acimutal (en la que varía θ). Esta base se relaciona con la canónica por el cambio de base
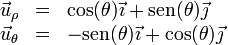 ó
ó 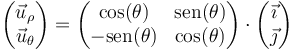
y su inverso
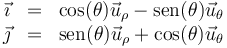 ó
ó 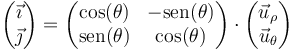
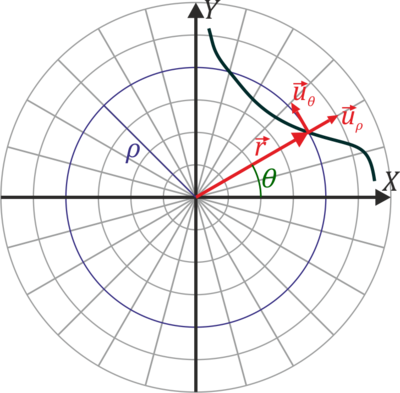
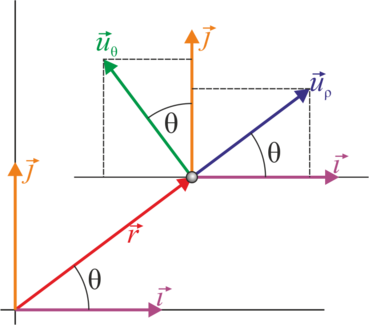
Los vectores unitarios en polares dependen de la posición. Aunque tengan el mismo nombre, el vector 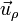 en un punto es diferente del vector
en un punto es diferente del vector 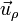 en otro. Por ello, hay que tener un cuidado infinito a la hora de operar con vectores en coordenadas polares.
en otro. Por ello, hay que tener un cuidado infinito a la hora de operar con vectores en coordenadas polares.
En particular, cuando consideramos el movimiento de una partícula, su posición, y por tanto los vectores de la base en polares, son funciones del tiempo. Por ello, cuando aparezca una derivada o una integral, habrá que tenerlos en cuenta. Sus derivadas respecto del tiempo valen
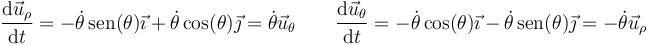
3.1 Posición en polares
Puesto que el vector 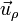 es el unitario en la dirección del vector de posición en el plano tenemos que la expresión de este en polares es
es el unitario en la dirección del vector de posición en el plano tenemos que la expresión de este en polares es
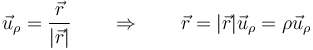
3.2 Velocidad en polares
la velocidad la calculamos derivando esta expresión respecto al tiempo, donde debemos recordar que también hay que derivar el vector unitario. Aplicamos la derivada de un producto

Esta expresión nos dice que la velocidad se compone de dos partes, una radial, debida a que la partícula se acerca o aleja del origen de coordenadas, y una acimutal, asociada al giro en torno a éste.
Por ejemplo, si consideramos una partícula describiendo un movimiento circular alrededor del origen,

y resulta la velocidad
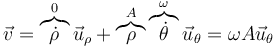
En un movimiento circular alrededor del origen la velocidad es puramente acimutal, ya que la partícula solo gira en torno al origen.
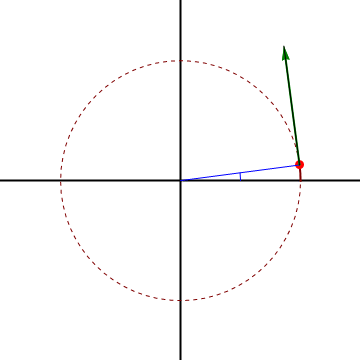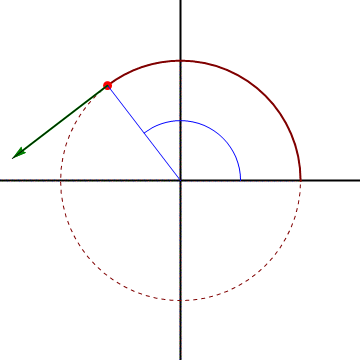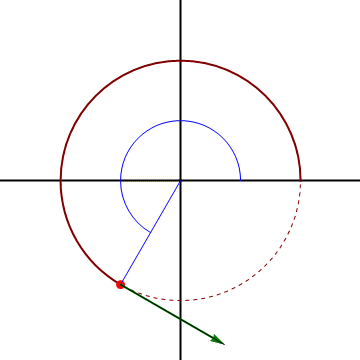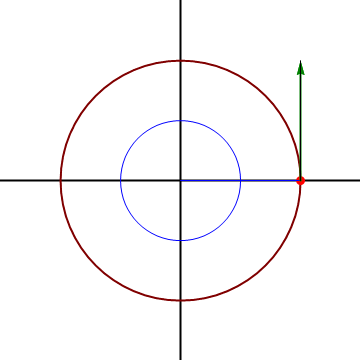
Sin embargo, el que la velocidad acimutal sea distinta de cero (que visto desde el origen se vea girar), no implica que el movimiento sea circular, ni siquiera curvo.
Consideremos el caso de una partícula que sigue un movimiento rectilíneo y uniforme a lo largo de una recta paralela al origen de forma que

La expresión de este movimiento en polares es

Las derivadas respecto al tiempo de estas dos magnitudes valen
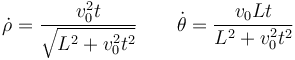
y esto nos da la velocidad instantánea
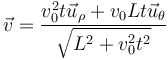
vemos que aunque el movimiento sea rectilíneo y uniforme, resulta una velocidad radial y una acimutal no nula. Para interpretarlo nos imaginamos a un observador situado en el origen de coordenadas, que apunte en todo momento a la partícula. Este observador ve a la partícula acercarse y alejarse (pasando por un mínimo justo cuando está en la perpendicular a la recta), y también ve cambiar la dirección de observación, lo que equivale a un giro.
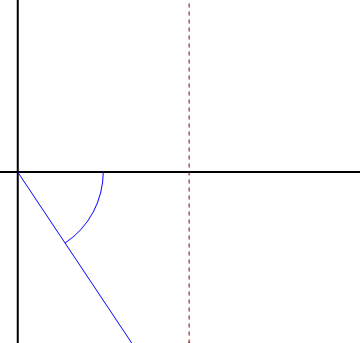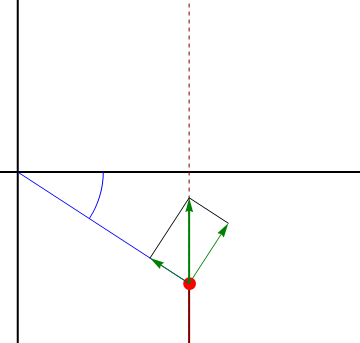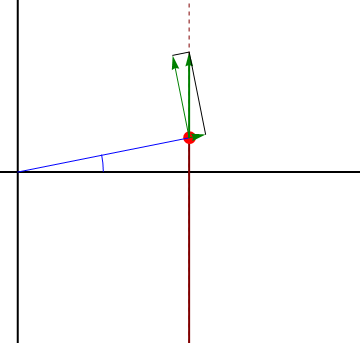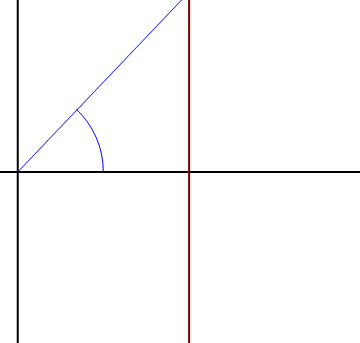
3.3 Aceleración en polares
Operando igualmente obtenemos la expresión de la aceleración en polares, solo que esta vez debemos derivar más términos y también el vector 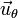
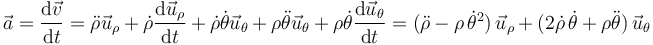
En el caso del movimiento circular tenemos que, para la coordenada radial
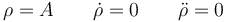
y para la acimutal

lo que nos da la aceleración lineal
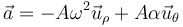
En general tendrá tanto componente radial (que en este caso coincide con la aceleración normal) como componente acimutal (que en este caso coincide con la tangencial).
En el caso del movimiento rectilíneo y uniforme, tras una serie de cálculos bastante laboriosos se llega a que

y por tanto
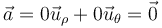
como corresponde a un movimiento rectilíneo y uniforme.
3.4 Resumen de expresiones
Los vectores de posición, velocidad y aceleración en este sistema quedan, por tanto,
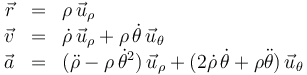
En coordenadas polares, la rapidez es igual a
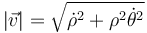
4 Movimiento circular
Puesto que los sistemas de referencia son arbitrarios, una vez que sabemos que un movimiento es circular, podemos tomar el origen de coordenadas en el centro de la circunferencia y los ejes de forma que la trayectoria esté contenida en el plano XY y con el origen de coordenadas en el centro de la circunferencia. En coordenadas polares, una circunferencia centrada en el origen se escribe simplemente

La ecuación vectorial de la trayectoria se reduce a

siendo la ley horaria
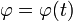
La velocidad de un movimiento circular es puramente acimutal,
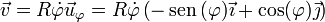
siendo la rapidez y el vector tangente

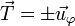
El signo variable depende del sentido de recorrido sobre la circunferencia. Por ejemplo, el movimiento de la lenteja de un péndulo es circular (aunque no complete una circunferencia) pero en su vaivén, el vector tangente unas veces coincide con el unitario en la dirección acimutal y otras es el opuesto.
La distancia medida sobre la curva



La velocidad angular va en la dirección normal al plano y es tal que al multiplicarla vectorialmente por  resulta la velocidad. Esto da
resulta la velocidad. Esto da

La aceleración de la partícula es
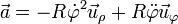
con componentes intrínsecas
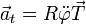

con el vector normal
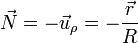
Por último, la aceleración angular viene dada por
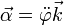
Con estos ejes, un movimiento circular uniforme corresponde a
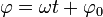
con ω constante.
5 Triedro de Frenet
5.1 Vectores tangente y normal
Al estar la velocidad contenida en el plano de movimiento, el vector tangente estará contenido en el mismo plano y formará un cierto ángulo variable θ con el eje OX
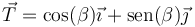
Al pasar el tiempo, este ángulo irá cambiando por lo que
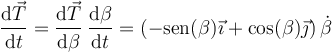
El primer factor es un vector unitario y ortogonal a  , esto es, se trata del vector normal
, esto es, se trata del vector normal  .
.

Nótese la similtud con la expresión de la base en coordenadas polares, que puede inducir a confusión. En coordenadas polares,  es el ámgulo que el vector de posición forma con el eje OX. En el triedro intrínseco, β es el ángulo que la velocidad forma con dicho eje.
es el ámgulo que el vector de posición forma con el eje OX. En el triedro intrínseco, β es el ángulo que la velocidad forma con dicho eje.
5.2 Vector binormal
Si multiplicamos vectorialmente el vector tangente y el vector normal obtenemos que el vector binormal es constante, como corresponde a un movimiento plano.
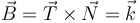
5.3 Interpretación del radio y el centro de curvatura
Si particularizamos para el caso del movimiento plano, es fácil dar un significado geométrico al radio de curvatura.
De la derivada temporal del vector tangente obtenemos
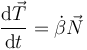
pero en un movimiento plano, la rapidez con que varía un ángulo es una velocidad angular, que para un movimiento circular equivale a la velocidad lineal dividida por el radio
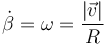
por lo que escribimos
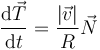
El radio de curvatura, R, equivale entonces al radio de la circunferencia que, en un instante dado, está describiendo a la partícula, o para ser más precisos, la circunferencia que más se aproxima a la trayectoria en dicho instante (misma posición, misma velocidad y misma aceleración). Esta circunferencia tangente se denomina circunferencia osculatriz. Su centro es el centro de curvatura.