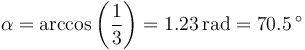Ángulo entre diagonales
De Laplace
(Diferencias entre revisiones)
| (Una edición intermedia no se muestra.) | |||
| Línea 3: | Línea 3: | ||
==Solución== | ==Solución== | ||
| - | Construimos un sistema | + | Construimos un sistema de referencia con origen en un vértice del cubo y con ejes los definidos por las tres aristas contiguas. |
Una de las diagonales es la que va del origen al vértice opuesto | Una de las diagonales es la que va del origen al vértice opuesto | ||
| Línea 11: | Línea 11: | ||
Otra de las diagonales es la que une otro par de vértices opuestos | Otra de las diagonales es la que une otro par de vértices opuestos | ||
| - | <center><math>B( | + | <center><math>B(b,0,0)\qquad C(0,b,b)\qquad\Rightarrow\qquad \overrightarrow{BC}=-b\vec{\imath}+b\vec{\jmath}+b\vec{k}</math></center> |
| + | |||
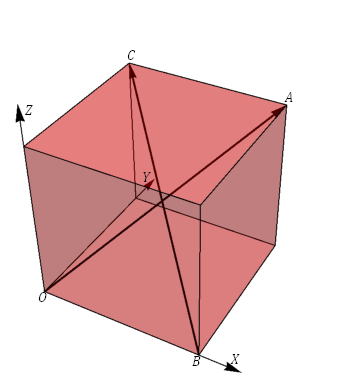
| + | <center>[[Archivo:cubo-diagonal.png]]</center> | ||
El coseno del ángulo que forman lo calculamos a partir del producto escalar | El coseno del ángulo que forman lo calculamos a partir del producto escalar | ||
| Línea 23: | Línea 25: | ||
y su producto escalar vale | y su producto escalar vale | ||
| - | <center><math>\overrightarrow{OA}\cdot\overrightarrow{BC}=b\cdot b + b\cdot | + | <center><math>\overrightarrow{OA}\cdot\overrightarrow{BC}=b\cdot(-b) + b\cdot b +b\cdot b=b^2</math></center> |
lo que nos da | lo que nos da | ||
última version al 16:17 1 oct 2015
1 Enunciado
Calcule el ángulo que forman dos diagonales de un cubo.
2 Solución
Construimos un sistema de referencia con origen en un vértice del cubo y con ejes los definidos por las tres aristas contiguas.
Una de las diagonales es la que va del origen al vértice opuesto
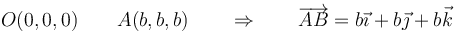
Otra de las diagonales es la que une otro par de vértices opuestos
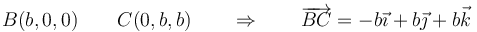
El coseno del ángulo que forman lo calculamos a partir del producto escalar
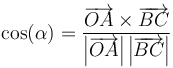
El módulo de ambos vectores vale lo mismo
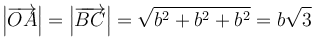
y su producto escalar vale
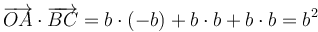
lo que nos da
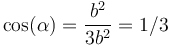
y de aquí hallamos el ángulo