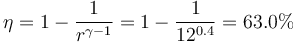Caso de ciclo Otto ideal
De Laplace
(Página creada con '==Enunciado== El funcionamiento de un motor de gasolina de 98 octanos con turbocompresor puede modelarse como un ciclo Otto ideal en el que el volumen máximo es de 2000\,cm\tss…') |
|||
| (9 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | El funcionamiento de un motor de gasolina de 98 octanos | + | El funcionamiento de un motor de gasolina de 98 octanos con turbocompresor puede modelarse como un ciclo Otto ideal en el que el volumen máximo es de 2000 cm³ y la mezcla (aire+gasolina, que puede tratarse como aire seco) entra a 150 kPa y 350 K. La relación de compresión es <math>r=12</math> y la mezcla tiene un poder calorífico de 800 kJ/kg. |
| - | con turbocompresor puede modelarse como un ciclo Otto ideal en el que el | + | |
| - | volumen máximo es de 2000 | + | |
| - | tratarse como aire seco) entra a 150 | + | |
| - | es | + | |
| - | + | # Calcule la presión, volumen y temperatura al final de cada paso del ciclo Otto. | |
| - | + | # Calcule el calor que entra, el que sale y el trabajo neto que realiza en un ciclo. | |
| - | paso del ciclo Otto. | + | # Halle el rendimiento de este motor de explosión. |
| - | + | ||
| - | que realiza en un ciclo. | + | |
| - | + | ||
| - | + | ||
Datos: | Datos: | ||
| - | + | ||
| - | R=8.314\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}\qquad\qquad | + | <center><math>R=8.314\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}\qquad\qquad |
P_m(\mbox{aire})=28.96\,\frac{\mathrm{g}}{\mathrm{mol}}\qquad\qquad | P_m(\mbox{aire})=28.96\,\frac{\mathrm{g}}{\mathrm{mol}}\qquad\qquad | ||
| - | \gamma(\mbox{aire})=1.4 | + | \gamma(\mbox{aire})=1.4</math></center> |
| - | \] | + | |
| + | ==Estados del sistema== | ||
| + | Este problema es casi idéntico en su desarrollo al ejemplo que aparece en el [[Ciclo_Otto_%28GIE%29#Ejemplo_pr.C3.A1ctico|tema de teoría]]. Se diferencia en los valores numéricos, pero poco más. No obstante, desarrollaremos aquí los cálculos igualmente. | ||
| + | |||
| + | [[Image:ciclo-otto.png|right]] | ||
| + | |||
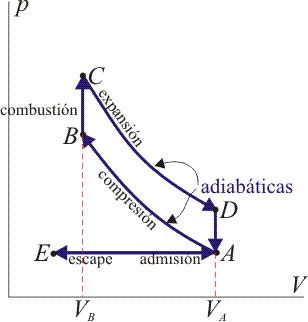
| + | El ciclo Otto ideal se compone de cuatro pasos: | ||
| + | |||
| + | ;A→B: Compresión adiabática | ||
| + | ;B→C: Calentamiento isócoro | ||
| + | ;C→D: Expansión adiabática | ||
| + | ;D→A: Enfriamiento isócoro | ||
| + | |||
| + | ===Estado A=== | ||
| + | En el estado A, tras la admisión de la mezcla, lo que tenemos es una masa de aire+gasolina, con las variables de estado: | ||
| + | |||
| + | <center><math>p_A=150\,\mathrm{kPa}=0.15\,\mathrm{MPa}\qquad\qquad T_A=350\,\mathrm{K}\qquad\qquad V_A=2000\,\mathrm{cm}^3</math></center> | ||
| + | |||
| + | El número de moles y la masa de la mezcla los hallamos aplicando la ley de los gases ideales | ||
| + | |||
| + | <center><math>n = \frac{p_AV_A}{RT_A}=0.103\,\mathrm{mol}\qquad\qquad m=nP_m=2.99\,\mathrm{g}</math></center> | ||
| + | |||
| + | ===Estado B=== | ||
| + | Tras la compresión adiabática, el volumen se reduce según la relación de compresión | ||
| + | |||
| + | <center><math>r=\frac{V_A}{V_B}\qquad\Rightarrow\qquad V_B=\frac{V_A}{r}=\frac{2000}{12}\mathrm{cm}^3=167\,\mathrm{cm}^3</math></center> | ||
| + | |||
| + | y la presión aumenta según la ley de Poisson | ||
| + | |||
| + | <center><math>p_AV_A^\gamma=P_BV_B^\gamma\qquad\Rightarrow\qquad p_B = p_A r^\gamma = 4.86\,\mathrm{MPa}</math></center> | ||
| + | |||
| + | La temperatura también se incrementa pero en menor medida | ||
| + | |||
| + | <center><math>T_AV_A^{\gamma-1}=T_BV_B^{\gamma-1}\qquad\Rightarrow\qquad T_B = T_A r^{\gamma-1} = 946\,\mathrm{K}</math></center> | ||
| + | |||
| + | ===Estado C=== | ||
| + | Tras la explosión de la chispa, el fluido se calienta bruscamente, sin cambiar su volumen | ||
| + | |||
| + | <center><math>V_C=V_B= 167\,\mathrm{cm}^3</math></center> | ||
| + | |||
| + | La cantidad de calor que se genera en la explosión la da el poder calorífico | ||
| + | |||
| + | <center><math>Q=qm = 800\,\frac{\mathrm{J}}{\mathrm{g}}\times 2.99\mathrm{g}=2390\,\mathrm{J}</math></center> | ||
| + | |||
| + | lo que produce el aumento de temperatura | ||
| + | |||
| + | <center><math>Q_\mathrm{in}=nc_v\,\Delta T\qquad \Delta T = \frac{Q_\mathrm{in}}{n c_v}=\frac{2390}{1.03\times 20.8}=1110\,\mathrm{K}</math></center> | ||
| + | |||
| + | siendo | ||
| + | |||
| + | <center><math>c_v=\frac{R}{\gamma-1}=20.8\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}</math></center> | ||
| + | |||
| + | esto da la temperatura de este estado | ||
| + | |||
| + | <center><math>T_C=T_B+\Delta T = 2060\,\mathrm{K}</math></center> | ||
| + | |||
| + | y la presión la hallamos mediante la ley de los gases ideales, que para volumen constante se reduce adiabática | ||
| + | |||
| + | <center><math>\frac{p_B}{T_B}=\frac{p_C}{T_C}\qquad\Rightarrow\qquad p_C=p_B\frac{T_C}{T_B}=10.6\,\mathrm{MPa}</math></center> | ||
| + | |||
| + | ===Estado D=== | ||
| + | En la expansión adiabática, el volumen vuelve a ser el máximo | ||
| + | |||
| + | <center><math>V_D=V_A=2000\,\mathrm{cm}^3</math></center> | ||
| + | |||
| + | mientras que la presión se reduce según la ley de Poisson | ||
| + | |||
| + | <center><math>p_D=\frac{p_C}{r^\gamma}=0.327\,\mathrm{MPa}</math></center> | ||
| + | |||
| + | y también se reduce la temperatura | ||
| + | |||
| + | <center><math>T_D=\frac{T_C}{r^{\gamma-1}}=763\,\mathrm{K}</math></center> | ||
| + | |||
| + | ===Resumen=== | ||
| + | Resumiendo, tenemos la siguiente tabla: | ||
| + | |||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | ! Estado | ||
| + | ! V (cm³) | ||
| + | ! p (MPa) | ||
| + | ! T (K) | ||
| + | |- | ||
| + | ! A | ||
| + | | 2000 | ||
| + | | 0.150 | ||
| + | | 350 | ||
| + | |- | ||
| + | ! B | ||
| + | | 167 | ||
| + | | 4.86 | ||
| + | | 946 | ||
| + | |- | ||
| + | ! C | ||
| + | | 167 | ||
| + | | 10.6 | ||
| + | | 2060 | ||
| + | |- | ||
| + | ! D | ||
| + | | 2000 | ||
| + | | 0.327 | ||
| + | | 763 | ||
| + | |} | ||
| + | |||
| + | |||
| + | ==Calor y trabajo== | ||
| + | El calor que entra en el calentamiento ya lo hemos calculado | ||
| + | |||
| + | <center><math>Q_\mathrm{in}=mq=2390\,\mathrm{J}</math></center> | ||
| + | |||
| + | mientras que el que sale se halla de manera similar | ||
| + | |||
| + | <center><math>Q_\mathrm{out}=nc_v(T_D-T_A)=1.03\times 20.8\times(763-350)\mathrm{J}=884\,\mathrm{J}</math></center> | ||
| + | |||
| + | El trabajo neto que sale es la diferencia entre el calor que entra y el que sale | ||
| + | |||
| + | <center><math>W_\mathrm{out,neto}=Q_\mathrm{in}-Q_\mathrm{out}=1504\,\mathrm{J}</math></center> | ||
| + | |||
| + | ==Rendimiento== | ||
| + | El rendimiento lo da el cociente entre el trabajo que obtenemos y el calor que nos cuesta | ||
| + | |||
| + | <center><math>\eta=\frac{W_\mathrm{out,neto}}{Q_\mathrm{in}}=0.630=63.0\%</math></center> | ||
| + | |||
| + | También podemos hallar este rendimiento a partir de la fórmula para un ciclo Otto ideal | ||
| + | |||
| + | <center><math>\eta = 1-\frac{1}{r^{\gamma-1}}=1-\frac{1}{12^{0.4}}=63.0\%</math></center> | ||
| + | |||
| + | [[Categoría:Problemas de máquinas térmicas (GIE)]] | ||
última version al 20:00 10 sep 2015
Contenido |
1 Enunciado
El funcionamiento de un motor de gasolina de 98 octanos con turbocompresor puede modelarse como un ciclo Otto ideal en el que el volumen máximo es de 2000 cm³ y la mezcla (aire+gasolina, que puede tratarse como aire seco) entra a 150 kPa y 350 K. La relación de compresión es r = 12 y la mezcla tiene un poder calorífico de 800 kJ/kg.
- Calcule la presión, volumen y temperatura al final de cada paso del ciclo Otto.
- Calcule el calor que entra, el que sale y el trabajo neto que realiza en un ciclo.
- Halle el rendimiento de este motor de explosión.
Datos:
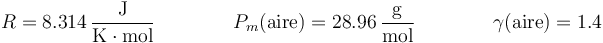
2 Estados del sistema
Este problema es casi idéntico en su desarrollo al ejemplo que aparece en el tema de teoría. Se diferencia en los valores numéricos, pero poco más. No obstante, desarrollaremos aquí los cálculos igualmente.
El ciclo Otto ideal se compone de cuatro pasos:
- A→B
- Compresión adiabática
- B→C
- Calentamiento isócoro
- C→D
- Expansión adiabática
- D→A
- Enfriamiento isócoro
2.1 Estado A
En el estado A, tras la admisión de la mezcla, lo que tenemos es una masa de aire+gasolina, con las variables de estado:
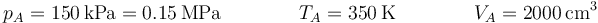
El número de moles y la masa de la mezcla los hallamos aplicando la ley de los gases ideales

2.2 Estado B
Tras la compresión adiabática, el volumen se reduce según la relación de compresión
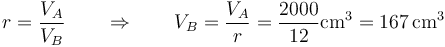
y la presión aumenta según la ley de Poisson

La temperatura también se incrementa pero en menor medida
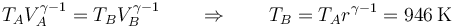
2.3 Estado C
Tras la explosión de la chispa, el fluido se calienta bruscamente, sin cambiar su volumen
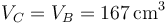
La cantidad de calor que se genera en la explosión la da el poder calorífico
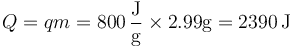
lo que produce el aumento de temperatura
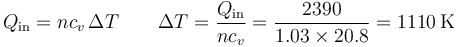
siendo
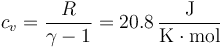
esto da la temperatura de este estado
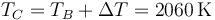
y la presión la hallamos mediante la ley de los gases ideales, que para volumen constante se reduce adiabática
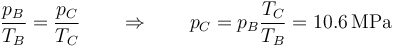
2.4 Estado D
En la expansión adiabática, el volumen vuelve a ser el máximo
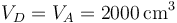
mientras que la presión se reduce según la ley de Poisson
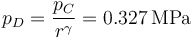
y también se reduce la temperatura
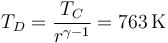
2.5 Resumen
Resumiendo, tenemos la siguiente tabla:
| Estado | V (cm³) | p (MPa) | T (K) |
|---|---|---|---|
| A | 2000 | 0.150 | 350 |
| B | 167 | 4.86 | 946 |
| C | 167 | 10.6 | 2060 |
| D | 2000 | 0.327 | 763 |
3 Calor y trabajo
El calor que entra en el calentamiento ya lo hemos calculado
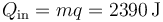
mientras que el que sale se halla de manera similar
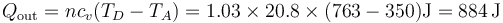
El trabajo neto que sale es la diferencia entre el calor que entra y el que sale
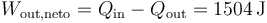
4 Rendimiento
El rendimiento lo da el cociente entre el trabajo que obtenemos y el calor que nos cuesta
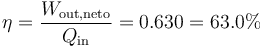
También podemos hallar este rendimiento a partir de la fórmula para un ciclo Otto ideal