Flujo de un campo vectorial
De Laplace
(→Ejemplo) |
(→Campo solenoidal) |
||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 50: | Línea 50: | ||
==Flujo a través de una superficie cerrada== | ==Flujo a través de una superficie cerrada== | ||
| + | ===Definición=== | ||
De manera análoga puede definirse el flujo a través de una superficie cerrada <math>\partial\tau</math> que es la frontera de un volumen <math>\tau</math>, como la integral | De manera análoga puede definirse el flujo a través de una superficie cerrada <math>\partial\tau</math> que es la frontera de un volumen <math>\tau</math>, como la integral | ||
| Línea 64: | Línea 65: | ||
===Ejemplo=== | ===Ejemplo=== | ||
Consideremos ahora el flujo del campo | Consideremos ahora el flujo del campo | ||
| + | <center> | ||
| + | <math>\mathbf{r}=x\mathbf{u}_x+y\mathbf{u}_y+z\mathbf{z}_z</math></center> | ||
| + | |||
| + | a través de una superficie cúbica de arista <math>2a</math> centrado en el origen y con lados paralelos a los ejes. | ||
| + | |||
| + | Por la simetría del sistema, el flujo a través de cada cara tendrá el mismo valor <math>\Phi_C</math> | ||
| + | |||
| + | <center><math>\Phi_T = 6\Phi_C\,</math> | ||
| + | </center> | ||
| + | |||
| + | A su vez, de nuevo por simetría, la contribución de cada cara es el cuádruple de la de un cuadrado como el que se vio en un [[#Ejemplo|apartado anterior]]. | ||
| + | |||
| + | <center><math>\Phi_C = 4\Phi_i</math></center> | ||
| + | |||
| + | Por tanto | ||
| + | |||
| + | <center> | ||
| + | <math>\Phi_T = 24a^3</math></center> | ||
===Campo solenoidal=== | ===Campo solenoidal=== | ||
| Línea 75: | Línea 94: | ||
<center><math>\oint_{\partial\tau} \mathbf{B}\cdot\mathrm{d}\mathbf{S}=0</math></center> | <center><math>\oint_{\partial\tau} \mathbf{B}\cdot\mathrm{d}\mathbf{S}=0</math></center> | ||
| - | + | Un ejemplo más desarrollado se encuentra en [[Cálculo_de_flujo|un problema]]. | |
[[Categoría:Fundamentos matemáticos]] | [[Categoría:Fundamentos matemáticos]] | ||
última version al 19:11 28 dic 2008
Contenido |
1 Introducción
2 Flujo de un campo uniforme en una sección ortogonal
Consideremos en primer lugar el caso de una tubería de sección S por la cual fluye agua con la misma velocidad v en todos sus puntos. Nos preguntamos por el caudal de la tubería, esto es, por la cantidad de agua (en volumen) que atraviesa una sección de la tubería en la unidad de tiempo. En un intervalo dt la cantidad de agua que atraviesa S es aquella que se encuentra a una distancia menor de 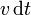 .
.


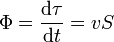
El caudal es igual al producto de la velocidad del líquido por la sección de la tubería. A mayor velocidad o mayor sección, mayor caudal. Este caudal es el flujo del campo vectorial  a través de la sección S.
a través de la sección S.
3 Flujo de un campo uniforme en una sección oblicua
Supongamos ahora la misma tubería, y la misma velocidad uniforme del líquido, pero tomando una sección oblicua de la tubería. El caudal que atraviesa esta nueva sección debe ser el mismo que antes, sin embargo, esta cantidad no puede ser igual a vS pues ahora S es mayor que antes.
Para extender la fórmula anterior a este caso observamos que no toda la velocidad atraviesa la superficie. Si en cada punto de la superficie descomponemos la velocidad en su componente normal a la superficie y su componente tangencial a ella, solo la primera contribuye al flujo, ya que la componente tangencial corresponde a que el líquido “resbale” sobre la superficie. Por tanto el flujo de agua a través de la superficie es
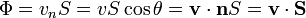
siendo θ el ángulo que forman la velocidad y el vector normal a la superficie y 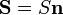 el vector superficie asociado a la sección de la tubería.
el vector superficie asociado a la sección de la tubería.
4 Flujo general de un campo a través de una superficie
4.1 Definición
La fórmula anterior tiene una extensión inmediata al caso de que tengamos una distribución no uniforme de velocidades (o de un campo vectorial, en general). Por ejemplo, el flujo real de un líquido en el interior de un capilar o tubo estrecho sigue un perfil parabólico (perfildePoiseuille). También podemos tener que la superficie a través de la cual se calcula el flujo no sea una sección plana.
En este caso general, simplemente hay que dividir la superficie en elementos diferenciales (que sí son planos), calcular el flujo a través de cada elemento y sumar todas las contribuciones.
Así se define el flujo de un campo vectorial  a través de una superficie abierta S como
a través de una superficie abierta S como
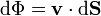

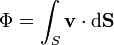
De esta definición hay que destacar:
- El flujo es una aplicación que actúa sobre campos vectoriales.
- El resultado es una cantidad escalar.
- El flujo tiene un signo.
- Es positivo si la hay más campo atravesando la superficie en el sentido de la normal a la superficie.
- Es negativo si el campo va predominantemente en sentido contrario a
 .
.
- Si el campo
 posee dimensiones físicas, las unidades de Φ son las de
posee dimensiones físicas, las unidades de Φ son las de  multiplicado por una superficie.
multiplicado por una superficie.
4.2 Ejemplo
Por ejemplo, sea el campo
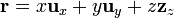
vamos a hallar el flujo a través de un cuadrado de lado a situado a una altura z = a con una esquina sobre el eje Z y lados paralelos a los ejes. Para este cuadrado
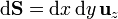

y el flujo vale
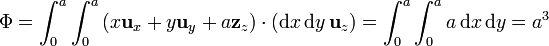
5 Flujo a través de una superficie cerrada
5.1 Definición
De manera análoga puede definirse el flujo a través de una superficie cerrada  que es la frontera de un volumen τ, como la integral
que es la frontera de un volumen τ, como la integral

En el caso de una superficie cerrada, el convenio es que la normal a la superficie se toma siempre hacia el exterior.
Por este convenio, el flujo a través de una superficie cerrada puede entenderse como la cantidad de campo que “escapa” del volumen.
- Si este flujo es positivo, se dice que el volumen τ contiene una cantidad neta de manantiales.
- Si este flujo es negativo, el volumen τ contiene una cantidad neta de sumideros.
- Si el flujo es nulo, en τ hay tantos manantiales como sumideros
5.2 Ejemplo
Consideremos ahora el flujo del campo
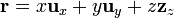
a través de una superficie cúbica de arista 2a centrado en el origen y con lados paralelos a los ejes.
Por la simetría del sistema, el flujo a través de cada cara tendrá el mismo valor ΦC
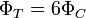
A su vez, de nuevo por simetría, la contribución de cada cara es el cuádruple de la de un cuadrado como el que se vio en un apartado anterior.
Por tanto
5.3 Campo solenoidal
Si el flujo de un campo 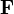 a través de cualquier superficie cerrada es nulo, entonces se dice que
a través de cualquier superficie cerrada es nulo, entonces se dice que 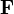 es solenoidal.
es solenoidal.
Un campo solenoidal se caracteriza porque sus líneas de campo no pueden ser tener extremos, ya que de tenerlos, el flujo alrededor de uno de ellos sería no nulo.
Un ejemplo real de campo solenoidal lo da el campo magnético  que para cualquier superficie cerrada verifica
que para cualquier superficie cerrada verifica
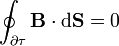
Un ejemplo más desarrollado se encuentra en un problema.





