Cuatro conductores paralelos
De Laplace
(→Estado tras la conexión) |
|||
| (7 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Se tiene un sistema de conductores en forma de bloques prismáticos cuadrados de lado <math>L=20\,\mathrm{cm}</math> de lado y grosor <math>b=1\,\mathrm{cm}</math>. Estos bloques se sitúan paralelamente de forma que entre el primero y el segundo hay un espacio <math>3a</math>; entre el 2º y el 3º hay <math>2a</math> y entre el 3 | + | Se tiene un sistema de conductores en forma de bloques prismáticos cuadrados de lado <math>L=20\,\mathrm{cm}</math> de lado y grosor <math>b=1\,\mathrm{cm}</math>. Estos bloques se sitúan paralelamente de forma que entre el primero y el segundo hay un espacio <math>3a</math>; entre el 2º y el 3º hay <math>2a</math> y entre el 3º y el 4º hay <math>a</math>, siendo <math>a=1\,\mathrm{mm}</math>. El espacio entre los conductores está lleno de un dieléctrico ideal de permitividad <math>\varepsilon=30\,\mathrm{pF}/\mathrm{m}</math>. |
El conductor 1 y el 4 se encuentran permanentemente a tierra. | El conductor 1 y el 4 se encuentran permanentemente a tierra. | ||
| Línea 26: | Línea 26: | ||
la sección de las placas y <math>d</math> la distancia entre placas, que es distinta en cada caso. Las capacidades de los tres condensadores son | la sección de las placas y <math>d</math> la distancia entre placas, que es distinta en cada caso. Las capacidades de los tres condensadores son | ||
| - | ;Entre el conductor 1 y el 2: | + | ;a. Entre el conductor 1 y el 2: |
<center><math>C_a=\frac{(30\,\mathrm{pF}/\mathrm{m})(0.04\,\mathrm{m}^2)}{0.003\,\mathrm{m}}=400\,\mathrm{pF}</math></center> | <center><math>C_a=\frac{(30\,\mathrm{pF}/\mathrm{m})(0.04\,\mathrm{m}^2)}{0.003\,\mathrm{m}}=400\,\mathrm{pF}</math></center> | ||
| - | ;Entre el 2 y el 3: | + | ;b. Entre el 2 y el 3: |
<center><math>C_b=\frac{(30\,\mathrm{pF}/\mathrm{m})(0.04\,\mathrm{m}^2)}{0.002\,\mathrm{m}}=600\,\mathrm{pF}</math></center> | <center><math>C_b=\frac{(30\,\mathrm{pF}/\mathrm{m})(0.04\,\mathrm{m}^2)}{0.002\,\mathrm{m}}=600\,\mathrm{pF}</math></center> | ||
| - | ;Entre el 3 y el 4: | + | ;c. Entre el 3 y el 4: |
<center><math>C_c=\frac{(30\,\mathrm{pF}/\mathrm{m})(0.04\,\mathrm{m}^2)}{0.001\,\mathrm{m}}=1200\,\mathrm{pF}</math></center> | <center><math>C_c=\frac{(30\,\mathrm{pF}/\mathrm{m})(0.04\,\mathrm{m}^2)}{0.001\,\mathrm{m}}=1200\,\mathrm{pF}</math></center> | ||
| Línea 39: | Línea 39: | ||
<center>[[Archivo:circuito-cuatro-bloques-01.png]]</center> | <center>[[Archivo:circuito-cuatro-bloques-01.png]]</center> | ||
| - | + | A partir de este circuito podemos construir un sistema de ecuaciones cuya solución nos de las cargas y potenciales que desconocemos, a partir de los datos que sí tenemos | |
| + | |||
| + | <center><math>V_1=V_4=0\,\mathrm{V}\qquad V_2=125\,\mathrm{V}\qquad Q_3=0\,\mathrm{nC}</math></center> | ||
| + | |||
| + | La carga de cada conductor equivale a la suma de las de las placas conectadas al nodo correspondiente. | ||
<center>[[Archivo:circuito-cuatro-bloques-02.png]]</center> | <center>[[Archivo:circuito-cuatro-bloques-02.png]]</center> | ||
| - | + | Por tanto | |
| - | <center><math>\ | + | <center><math>\begin{array}{rcl} |
| + | Q_1 & = & C_a(V_1-V_2) \\ | ||
| + | Q_2 & = & C_a(V_2-V_1) + C_b(V_2-V_3) \\ | ||
| + | Q_3 & = & C_b(V_3-V_2)+C_c(V_3-V_4) \\ | ||
| + | Q_4 & = & C_c(V_4-V_3) | ||
| + | \end{array}</math></center> | ||
| - | + | Sustituimos los datos y los valores de las capacidades y queda el sistema (con la carga en nC y el potencial en V) | |
| - | <center><math> | + | <center><math>\begin{array}{rcl} |
| + | Q_1 & = & 0.4(0-125)= -50 \\ | ||
| + | Q_2 & = & 0.4(125-0) + 0.6(125-V_3) = 125-0.6V_3\\ | ||
| + | 0 & = & 0.6(V_3-125)+1.2(V_3-0)= 1.8V_3-75 \\ | ||
| + | Q_4 & = & 1.2(0-V_3)=-1.2V_3 | ||
| + | \end{array}</math></center> | ||
| - | + | e aquí es inmediato el valor de <math>Q_1</math> | |
| - | <center><math> | + | <center><math>Q_1=-50\,\mathrm{nC}</math></center> |
| - | + | y el de <math>V_3</math> | |
| - | <center><math> | + | <center><math>V_3=\frac{75}{1.8}\,\mathrm{V}=41.7\,\mathrm{V}</math></center> |
| - | + | Conocido este dato hallamos <math>Q_4</math> | |
| - | <center><math>Q_4= | + | <center><math>Q_4 = -1.2\times 41.7\,\mathrm{nC}=-50\,\mathrm{nC}</math></center> |
| - | + | y <math>Q_2</math> | |
| - | <center><math> | + | <center><math>Q_2= 125-0.6\times 41.7 = 100\,\mathrm{nC}</math></center> |
Tabulamos todos los resultados | Tabulamos todos los resultados | ||
| Línea 92: | Línea 106: | ||
|} | |} | ||
| - | Una forma alternativa de llegar a este resultado es | + | Una forma alternativa de llegar a este resultado es reduciendo el circuito equivalente. |
| + | Sin cambiar las conexiones, podemos dibujarlo como | ||
| - | <center> | + | <center>[[Archivo:circuito-cuatro-bloques-03.png]]</center> |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | Dado que el conductor 3 está descargado, los condensadores b y c están en serie, cumpliendo su capacidad equivalente | |
| - | <center><math> | + | <center><math>\frac{1}{C_{bc}}=\frac{1}{C_b}+\frac{1}{C_c}=\frac{1}{600\,\mathrm{pF}}+\frac{1}{1200\,\mathrm{pF}}=\frac{1}{400\,\mathrm{pF}}\qquad\Rightarrow\qquad C_{bc}=400\,\mathrm{pF}</math></center> |
| - | + | Este condensador está en paralelo con el a, siendo la capacidad equivalente de la asociación completa | |
| - | <center><math> | + | <center><math>C_{abc}=C_a+C_{bc}=800\,\mathrm{pF}</math></center> |
| - | y | + | Esto nos da la carga del conductor 2, que corresponde a la placa positiva de este conductor equivalente |
| + | |||
| + | <center><math>Q_2=C_{abc}(V_2-0) = 800\,\mathrm{pF}\times 125\,\mathrm{V}=100\,\mathrm{nC}</math></center> | ||
| + | |||
| + | El conductor 1 corresponde a la placa negativa del condensador a, por lo que tiene una carga | ||
| + | |||
| + | <center><math>Q_1=C_a(0-V_0) = 400\,\mathrm{pF}(-125\,\mathrm{V})=-50\,\mathrm{nC}</math></center> | ||
| + | |||
| + | Análogamente, el conductar 4 es la placa negativa del condensador bc | ||
| + | |||
| + | <center><math>Q_4=C_{bc}(0-V_0) = 400\,\mathrm{pF}(-125\,\mathrm{V})=-50\,\mathrm{nC}</math></center> | ||
| + | |||
| + | Ya tenemos la carga de los cuatro conductores y el potencial de tres de ellos. Queda hallar el potencial del conductor 3. Éste lo sacamos de que este conductor es la placa positiva del condensador c | ||
| + | |||
| + | <center><math>Q_4=C_c(V_4-V_3) \qquad\Rightarrow\qquad -50\,\mathrm{nC}=1200\,\mathrm{pF}(0-V_3)\qquad\Rightarrow\qquad V_3 = 41.7\,\mathrm{V}</math></center> | ||
| + | |||
| + | ==Campo y cargas en cada superficie== | ||
| + | ===Cargas de cada superficie=== | ||
| + | En los cálculos anterios hemos obtenido la carga neta de cada conductor, pero podemos determinar la carga de cada superficie observando que cada una es una placa de un condensador plano. A partir de la diferencia de potencial entre placas podemos hallar estas cargas en todos los casos como | ||
| + | |||
| + | <center><math>Q_{i}=C_{ij}(V_i-V_j)</math></center> | ||
| + | |||
| + | siendo <math>Q_i</math> la carga de la placa i, <math>C_{ij}</math> la capacidad del condensador que ésta forma con la placa j y <math>(V_i-V_j)</math> la diferencia de potencial entre las dos. No obstante, existe más de una forma de hallar estas cargas, muchas veces por simples razonamientos de sumas y restas. | ||
| + | |||
| + | ;Conductor 1: Su placa exterior está descargada. La placa que da al condensador a almacena una carga | ||
| + | |||
| + | <center><math>Q_{1a}=C_a(V_1-V_2)=-50\,\mathrm{nC}</math></center> | ||
| + | |||
| + | :que coincide por supuesto con la total del conductor. | ||
| + | |||
| + | ;Conductor 2: La cara que da al condensador a es opuesta a la que acabamos de hallar | ||
| + | |||
| + | <center><math>Q_{2a}=-Q_{1a}=C_a(V_2-V_1)=+50\,\mathrm{nC}</math></center> | ||
| + | |||
| + | :y la que da al conductor b es el resto de la carga del condensador | ||
| + | |||
| + | <center><math>Q_{2b}=Q_2-Q_{2a}=+50\,\mathrm{nC}</math></center> | ||
| + | |||
| + | ;Conductor 3: La cara que da al condensador b es la opuesta a esta | ||
| + | |||
| + | <center><math>Q_{3b}=-Q_{2b}=-50\,\mathrm{nC}</math></center> | ||
| + | |||
| + | :y puesto que el conductor 3 está descargado, la carga de la otra cara debe anular a ésta | ||
| + | |||
| + | <center><math>Q_{3c}=Q_3-Q_{3b}=0-(-50\,\mathrm{nC})=+50\,\mathrm{nC}</math></center> | ||
| + | |||
| + | ;Conductor 4: Su carga está toda en el condensador c y vale | ||
| + | |||
| + | <center><math>Q_{4c}=-Q_{3c}=-50\,\mathrm{nC}</math></center> | ||
| + | |||
| + | ===Campo entre las placas=== | ||
| + | En un condensador plano, el campo puede hallarse a partir de la diferencia de potencial entre las placas | ||
| + | |||
| + | <center><math>\vec{E}=\frac{V_i-V_j}{d}\vec{u}_{ij}</math></center> | ||
| + | |||
| + | siendo <math>\vec{u}_{ij}</math> el vector unitario que apunta en el sentido de la placa i a la j. | ||
| + | |||
| + | Alternativamente, puede hallarse el campo, que en un condensador plano es uniforme, por su relación con la carga superficial (también uniforme) | ||
| + | |||
| + | <center><math>\vec{E}=\frac{\sigma_s}{\varepsilon}\vec{n}=\frac{Q_i}{\varepsilon L^2}\vec{u}_{ij}</math></center> | ||
| + | |||
| + | Por cualquiera de los dos métodos obtenemos los siguientes resultados: | ||
| + | |||
| + | ;Entre el conductor 1 y el 2: | ||
| + | |||
| + | <center><math>\vec{E}_a=\frac{V_1-V_2}{3a}\vec{\imath}=-\frac{125\,\mathrm{V}}{0.003\,\mathrm{m}}\vec{\imath}=-41.7\vec{\imath}\frac{\mathrm{kV}}{\mathrm{m}}</math></center> | ||
| + | |||
| + | ;Entre el 2 y el 3: | ||
| + | |||
| + | <center><math>\vec{E}_b=\frac{V_2-V_3}{2a}\vec{\imath}=\frac{(125-41.7)\,\mathrm{V}}{0.002\,\mathrm{m}}\vec{\imath}=+41.7\vec{\imath}\frac{\mathrm{kV}}{\mathrm{m}}</math></center> | ||
| + | |||
| + | ;Entre el 3 y el 4: | ||
| + | |||
| + | <center><math>\vec{E}_c=\frac{V_3-V_4}{a}\vec{\imath}=\frac{41.7\,\mathrm{V}}{0.001\,\mathrm{m}}\vec{\imath}=+41.7\vec{\imath}\frac{\mathrm{kV}}{\mathrm{m}}</math></center> | ||
| + | |||
| + | Aunque el módulo es el mismo en las tres regiones, el sentido no lo es, ya que el campo siempre va de más a menos potencial, por lo que en la región a va de derecha a izquierda y en las otras dos de izquierda a derecha. | ||
| + | |||
| + | ==Estado tras la conexión== | ||
| + | Cuando el interruptor pasa de la posición A a la B, deja de estar conectado a la fuente de tensión, por lo que su potencial deja de estar fijado y pasa a tener un valor desconocido por ahora. | ||
| + | |||
| + | Por otro lado, el conductor 2 se une al 3, lo que provoca que se produzca un trasvase de carga de uno al otro, debido a la diferencia de potencial entre ellos. Este flujo de carga continúa hasta que se igualan los potenciales de los dos conductores y vuelve a alcanzarse el equilibrio electrostático. Dado que se ha acumulado carga en el conductor 3, tampoco concemos por ahora el valor de la carga de este conductor. | ||
| + | |||
| + | Con estas dos nuevas incógnitas, nuestro sistema de ecuaciones queda, midiendo la carga en nC y el potencial en V, | ||
<center><math>\begin{array}{rcl} | <center><math>\begin{array}{rcl} | ||
| - | Q_1 & = & 0.4(0- | + | Q_1 & = & 0.4(0-V_2)=-0.4V_2 \\ |
| - | Q_2 & = & 0. | + | Q_2 & = & 0.4V_2 + 0.6(V_2-V_3) = V_2-0.6V_3\\ |
| - | + | Q_3 & = & 0.6(V_3-V_2)+1.2(V_3-0)= 1.8V_3-0.6V_2 \\ | |
Q_4 & = & 1.2(0-V_3)=-1.2V_3 | Q_4 & = & 1.2(0-V_3)=-1.2V_3 | ||
\end{array}</math></center> | \end{array}</math></center> | ||
| - | + | A estas ecuaciones hay que añadir que los conductores 2 y 3 están al mismo potencial | |
| - | <center><math> | + | <center><math>V_2 = V_3\,</math></center> |
| - | y el de | + | y que la carga que se redistribuye entre ellos es la misma que había en el conductor 2 antes de la conexión |
| - | <center><math> | + | <center><math>Q_2+Q_3=100\,\mathrm{nC}</math></center> |
| - | + | Sumando la segunda y tercera ecuación del sistema de 4 ecuaciones queda | |
| - | <center><math> | + | <center><math>100 = Q_2+Q_3=0.4V_2+1.2V_3= 1.6V_2\,</math></center> |
| - | + | de donde | |
| - | <center><math> | + | <center><math>V_2=V_3 = 62.5\,\mathrm{V}</math></center> |
| - | + | Con esto el cálculo de las cargas es inmediato. Sustituyendo los voltajes llegamos a | |
| + | <center><math>Q_1= -25\,\mathrm{nC}\qquad\qquad Q_2=+25\,\mathrm{nC}\qquad\qquad Q_3=+75\,\mathrm{nC}\qquad\qquad Q_4=-75\,\mathrm{nC}</math></center> | ||
| + | |||
| + | Tabulando los resultados: | ||
| - | |||
{| class="bordeado" | {| class="bordeado" | ||
|- | |- | ||
| Línea 145: | Línea 239: | ||
|- | |- | ||
| 1 | | 1 | ||
| - | | - | + | | -25 |
| 0 | | 0 | ||
|- | |- | ||
| 2 | | 2 | ||
| - | | | + | | 25 |
| 62.5 | | 62.5 | ||
|- | |- | ||
| 3 | | 3 | ||
| - | | | + | | 75 |
| 62.5 | | 62.5 | ||
|- | |- | ||
| 4 | | 4 | ||
| - | | - | + | | -75 |
| 0 | | 0 | ||
|} | |} | ||
| + | |||
| + | Alternativamente, puede emplearse el circuito equivalente. | ||
| + | |||
| + | <center>[[Archivo:circuito-cuatro-bloques-04.png]]</center> | ||
| + | |||
| + | Conectar los conductores 2 y 3 equivale a cortocircuitar el condensador b, ya que sus dos placas están unidas por un cable. En ese caso, el condensador b es como si no estuviera y el sistema se reduce a dos condensadores en paralelo, siendo la capacidad equivalente | ||
| + | |||
| + | <center><math>C_{ac}=C_a+C_c = 400\,\mathrm{pF}+1200\,\mathrm{pF}=1600\,\mathrm{pF}</math></center> | ||
| + | |||
| + | De aquí obtenemos el potencial del conductor 2 (y del 3) ya que conocemos su carga | ||
| + | |||
| + | <center><math>V_2=V_3=\frac{100\,\mathrm{nC}}{1600\,\mathrm{pF}}=62.5\,\mathrm{V}</math></center> | ||
| + | |||
| + | La carga del conductor 1 es la negativa del conductor abc} | ||
| + | |||
| + | <center><math>Q_1=C_a(0-V_2) = -0.4\times 62.5=-25\,\mathrm{nC}</math></center> | ||
| + | |||
| + | y la del conductor 2 es la positiva de este mismo condensador | ||
| + | |||
| + | <center><math>Q_2=-Q_1 = +25\,\mathrm{nC}</math></center> | ||
| + | |||
| + | Análogamente, la carga del conductor 4 es la negativa del condensador c | ||
| + | |||
| + | <center><math>Q_4=C_c(0-V_3) = -1.2\times 62.5=-75\,\mathrm{nC}</math></center> | ||
| + | |||
| + | y la del 3 la positiva de este mismo condensador | ||
| + | |||
| + | <center><math>Q_3=-Q_4=+75\,\mathrm{nC}</math></center> | ||
==Balance energético== | ==Balance energético== | ||
| + | La energía de un sistema de conductores viene dada por el sumatorio | ||
| + | |||
| + | <center><math>U_\mathrm{e}=\frac{1}{2}\sum_i Q_i V_i</math></center> | ||
| + | |||
| + | o, alternativamente, dado el sistema de condensadores equivalente | ||
| + | |||
| + | <center><math>U_\mathrm{e}=\frac{1}{2}\sum_k C_k(\Delta V_k)^2</math></center> | ||
| + | |||
| + | En nuestro caso esto da | ||
;Antes de la conexión | ;Antes de la conexión | ||
| - | <center><math>U_{\mathrm{e}i}=6.25\,\mu\mathrm{J}</math></center> | + | |
| + | <center><math>U_{\mathrm{e}i}=\frac{1}{2}Q_1\cdot 0 + \frac{1}{2}(100\,\mathrm{nC})(125\,\mathrm{V})+\frac{1}{2}0\cdot V_3+\frac{1}{2}Q_4\cdot 0 = 6.25\,\mu\mathrm{J}</math></center> | ||
;Después de la conexión | ;Después de la conexión | ||
<center><math>U_{\mathrm{e}f}=3.125\,\mu\mathrm{J}</math></center> | <center><math>U_{\mathrm{e}f}=3.125\,\mu\mathrm{J}</math></center> | ||
| - | ;Energía disipada | + | ;Energía disipada: Esta es la diferencia entre las dos cantidades |
<center><math>\Delta U = -3.125\,\mu\mathrm{J}</math></center> | <center><math>\Delta U = -3.125\,\mu\mathrm{J}</math></center> | ||
| + | |||
| + | La diferencia es negativa ya que se pierde energía. Esta energía disipada se va por efecto Joule en la resistencia del cable de conexión. | ||
última version al 17:28 17 sep 2014
Contenido |
1 Enunciado
Se tiene un sistema de conductores en forma de bloques prismáticos cuadrados de lado 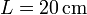 de lado y grosor
de lado y grosor 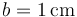 . Estos bloques se sitúan paralelamente de forma que entre el primero y el segundo hay un espacio 3a; entre el 2º y el 3º hay 2a y entre el 3º y el 4º hay a, siendo
. Estos bloques se sitúan paralelamente de forma que entre el primero y el segundo hay un espacio 3a; entre el 2º y el 3º hay 2a y entre el 3º y el 4º hay a, siendo 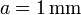 . El espacio entre los conductores está lleno de un dieléctrico ideal de permitividad
. El espacio entre los conductores está lleno de un dieléctrico ideal de permitividad 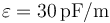 .
.
El conductor 1 y el 4 se encuentran permanentemente a tierra.
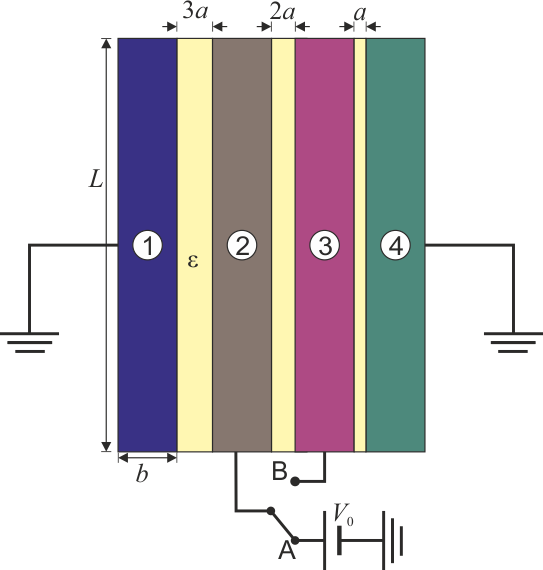
Inicialmente el interruptor se encuentra en la posición A, de forma que el conductor 2 se encuentra a un potencial 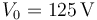 $, mientras que el 3 está aislado y descargado.
$, mientras que el 3 está aislado y descargado.
- Calcule el potencial del conductor 3, así como las cargas netas en cada uno de los cuatro conductores.
- Halle el campo eléctrico en cada uno de los espacios entre conductores, y las cargas almacenadas en cada una de las superficies conductoras
- Suponga que bruscamente se pasa el interruptor de la posición A a la B, conectando los conductores 2 y 3, ¿cómo quedan en ese caso las cargas y potenciales de los diferentes conductores, así como las cargas de cada una de las superficies?
- Halle la energía almacenada en el sistema antes y después de mover el interruptor.
¿Cuánta energía se disipa en el proceso?, ¿cómo puede haber desaparecido esta energía?
2 Potenciales y cargas iniciales
La forma más sencilla de resolver este problema es mediante un circuito equivalente.
Para construir este circuito sustituimos cada conductor por un nodo. Cada par de placas enfrentadas forma un condensador plano, de capacidad
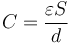
siendo
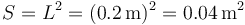
la sección de las placas y d la distancia entre placas, que es distinta en cada caso. Las capacidades de los tres condensadores son
- a. Entre el conductor 1 y el 2
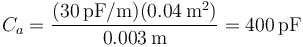
- b. Entre el 2 y el 3
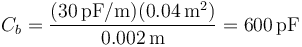
- c. Entre el 3 y el 4
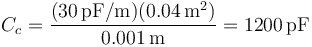
El circuito equivalente al sistema sería entonces el siguiente:
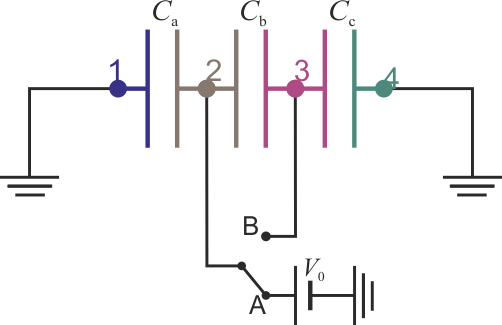
A partir de este circuito podemos construir un sistema de ecuaciones cuya solución nos de las cargas y potenciales que desconocemos, a partir de los datos que sí tenemos
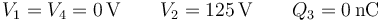
La carga de cada conductor equivale a la suma de las de las placas conectadas al nodo correspondiente.
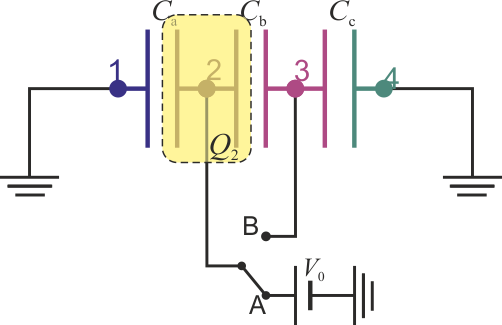
Por tanto
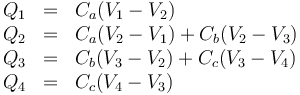
Sustituimos los datos y los valores de las capacidades y queda el sistema (con la carga en nC y el potencial en V)
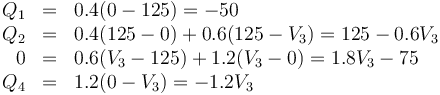
e aquí es inmediato el valor de Q1
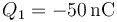
y el de V3
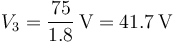
Conocido este dato hallamos Q4
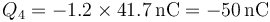
y Q2
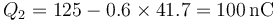
Tabulamos todos los resultados
| Conductor | Q (nC) | V (V) |
|---|---|---|
| 1 | -50 | 0 |
| 2 | 100 | 125 |
| 3 | 0 | 41.7 |
| 4 | -50 | 0 |
Una forma alternativa de llegar a este resultado es reduciendo el circuito equivalente. Sin cambiar las conexiones, podemos dibujarlo como
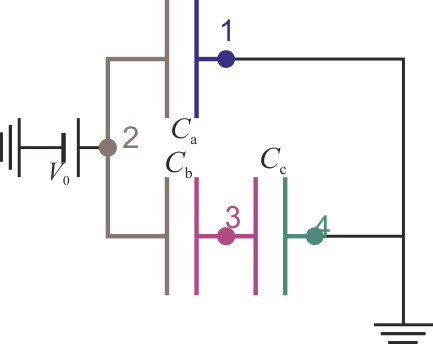
Dado que el conductor 3 está descargado, los condensadores b y c están en serie, cumpliendo su capacidad equivalente
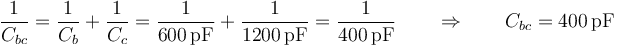
Este condensador está en paralelo con el a, siendo la capacidad equivalente de la asociación completa
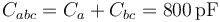
Esto nos da la carga del conductor 2, que corresponde a la placa positiva de este conductor equivalente
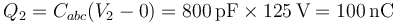
El conductor 1 corresponde a la placa negativa del condensador a, por lo que tiene una carga
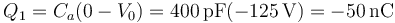
Análogamente, el conductar 4 es la placa negativa del condensador bc
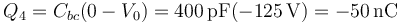
Ya tenemos la carga de los cuatro conductores y el potencial de tres de ellos. Queda hallar el potencial del conductor 3. Éste lo sacamos de que este conductor es la placa positiva del condensador c
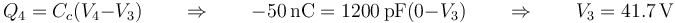
3 Campo y cargas en cada superficie
3.1 Cargas de cada superficie
En los cálculos anterios hemos obtenido la carga neta de cada conductor, pero podemos determinar la carga de cada superficie observando que cada una es una placa de un condensador plano. A partir de la diferencia de potencial entre placas podemos hallar estas cargas en todos los casos como
siendo Qi la carga de la placa i, Cij la capacidad del condensador que ésta forma con la placa j y (Vi − Vj) la diferencia de potencial entre las dos. No obstante, existe más de una forma de hallar estas cargas, muchas veces por simples razonamientos de sumas y restas.
- Conductor 1
- Su placa exterior está descargada. La placa que da al condensador a almacena una carga
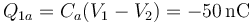
- que coincide por supuesto con la total del conductor.
- Conductor 2
- La cara que da al condensador a es opuesta a la que acabamos de hallar
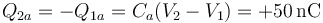
- y la que da al conductor b es el resto de la carga del condensador
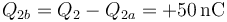
- Conductor 3
- La cara que da al condensador b es la opuesta a esta
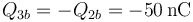
- y puesto que el conductor 3 está descargado, la carga de la otra cara debe anular a ésta
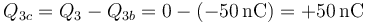
- Conductor 4
- Su carga está toda en el condensador c y vale
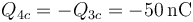
3.2 Campo entre las placas
En un condensador plano, el campo puede hallarse a partir de la diferencia de potencial entre las placas
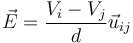
siendo 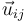 el vector unitario que apunta en el sentido de la placa i a la j.
el vector unitario que apunta en el sentido de la placa i a la j.
Alternativamente, puede hallarse el campo, que en un condensador plano es uniforme, por su relación con la carga superficial (también uniforme)
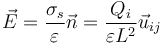
Por cualquiera de los dos métodos obtenemos los siguientes resultados:
- Entre el conductor 1 y el 2
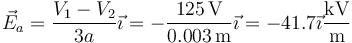
- Entre el 2 y el 3
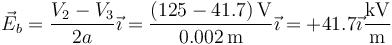
- Entre el 3 y el 4
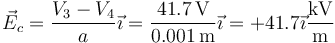
Aunque el módulo es el mismo en las tres regiones, el sentido no lo es, ya que el campo siempre va de más a menos potencial, por lo que en la región a va de derecha a izquierda y en las otras dos de izquierda a derecha.
4 Estado tras la conexión
Cuando el interruptor pasa de la posición A a la B, deja de estar conectado a la fuente de tensión, por lo que su potencial deja de estar fijado y pasa a tener un valor desconocido por ahora.
Por otro lado, el conductor 2 se une al 3, lo que provoca que se produzca un trasvase de carga de uno al otro, debido a la diferencia de potencial entre ellos. Este flujo de carga continúa hasta que se igualan los potenciales de los dos conductores y vuelve a alcanzarse el equilibrio electrostático. Dado que se ha acumulado carga en el conductor 3, tampoco concemos por ahora el valor de la carga de este conductor.
Con estas dos nuevas incógnitas, nuestro sistema de ecuaciones queda, midiendo la carga en nC y el potencial en V,
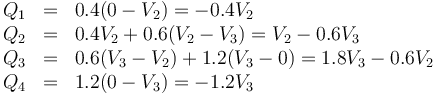
A estas ecuaciones hay que añadir que los conductores 2 y 3 están al mismo potencial
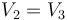
y que la carga que se redistribuye entre ellos es la misma que había en el conductor 2 antes de la conexión
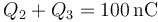
Sumando la segunda y tercera ecuación del sistema de 4 ecuaciones queda
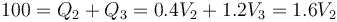
de donde
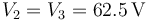
Con esto el cálculo de las cargas es inmediato. Sustituyendo los voltajes llegamos a

Tabulando los resultados:
| Conductor | Q (nC) | V (V) |
|---|---|---|
| 1 | -25 | 0 |
| 2 | 25 | 62.5 |
| 3 | 75 | 62.5 |
| 4 | -75 | 0 |
Alternativamente, puede emplearse el circuito equivalente.
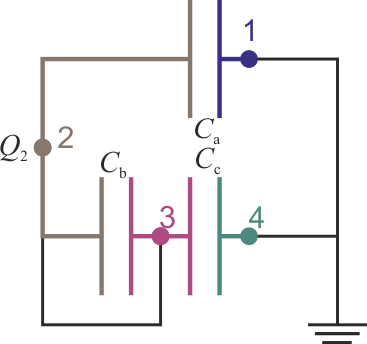
Conectar los conductores 2 y 3 equivale a cortocircuitar el condensador b, ya que sus dos placas están unidas por un cable. En ese caso, el condensador b es como si no estuviera y el sistema se reduce a dos condensadores en paralelo, siendo la capacidad equivalente
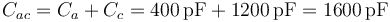
De aquí obtenemos el potencial del conductor 2 (y del 3) ya que conocemos su carga
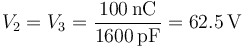
La carga del conductor 1 es la negativa del conductor abc}
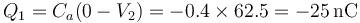
y la del conductor 2 es la positiva de este mismo condensador
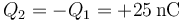
Análogamente, la carga del conductor 4 es la negativa del condensador c
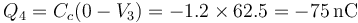
y la del 3 la positiva de este mismo condensador
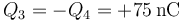
5 Balance energético
La energía de un sistema de conductores viene dada por el sumatorio
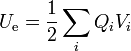
o, alternativamente, dado el sistema de condensadores equivalente
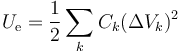
En nuestro caso esto da
- Antes de la conexión
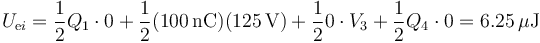
- Después de la conexión
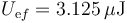
- Energía disipada
- Esta es la diferencia entre las dos cantidades
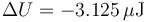
La diferencia es negativa ya que se pierde energía. Esta energía disipada se va por efecto Joule en la resistencia del cable de conexión.





