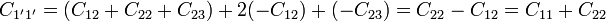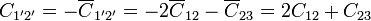Sistema simétrico de cuatro conductores

De Laplace

Revisión de 18:25 16 dic 2008 (ver código fuente) Antonio (Discusión | contribuciones) (→Solución) ← Edición más antigua		última version al 20:40 10 ene 2010 (ver código fuente) Antonio (Discusión | contribuciones) (→Mediante un circuito equivalente)
(18 ediciones intermedias no se muestran.)
Línea 6:		Línea 6:
	Suponga que mediante finos hilos conductores se conecta el conductor 1 con el 3, y el 2 con el 4 (estos cables atraviesan, sin hacer contacto, los conductores 2 y 3). ¿Cómo queda la nueva matriz de capacidades a partir de la matriz del sistema original?		Suponga que mediante finos hilos conductores se conecta el conductor 1 con el 3, y el 2 con el 4 (estos cables atraviesan, sin hacer contacto, los conductores 2 y 3). ¿Cómo queda la nueva matriz de capacidades a partir de la matriz del sistema original?
-	==Solución==	+	==Introducción==
	En este problema no se trata de establecer los valores exactos de los coeficientes, sino algunas de sus propiedades. Por ello, la geometría exacta es menos importante que la ''topología'' del problema, esto es, qué conductores están contenidos por cuáles.		En este problema no se trata de establecer los valores exactos de los coeficientes, sino algunas de sus propiedades. Por ello, la geometría exacta es menos importante que la ''topología'' del problema, esto es, qué conductores están contenidos por cuáles.
		+	==Simetría 1–4 y 2–3==
	Dada la simetría especular del sistema, lo más inmediato es determinar cuáles de los coeficientes de capacidad son iguales entre sí. De		Dada la simetría especular del sistema, lo más inmediato es determinar cuáles de los coeficientes de capacidad son iguales entre sí. De
	entrada, la matriz de coeficientes de capacidad es simétrica. Los coeficientes serán iguales si hacemos la permutación <math>1\leftrightarrow 4</math> y <math>2\leftrightarrow 3</math>. Obtenemos las siguientes equivalencias		entrada, la matriz de coeficientes de capacidad es simétrica. Los coeficientes serán iguales si hacemos la permutación <math>1\leftrightarrow 4</math> y <math>2\leftrightarrow 3</math>. Obtenemos las siguientes equivalencias
-	<center><math>C_{11} = C_{44}\,</math>{{qquad}}{{qquad}}<math>C_{22} = C_{33}\,</math>{{qquad}}{{qquad}}<math>C_{12} = C_{21} = C_{34} = C_{43}</math>{{qquad}}{{qquad}}<math>C_{13} = C_{31}  = C_{42} = C_{24}</math>{{qquad}}<math>C_{14} = C_{41}</math>{{qquad}}{{qquad}}<math>C_{23} = C_{32}</math></center>	+	<center><math>C_{11} = C_{44}\,</math>{{qquad}}{{qquad}}<math>C_{22} = C_{33}\,</math>{{qquad}}{{qquad}}<math>C_{12} = C_{21} = C_{34} = C_{43}\,</math>{{qquad}}{{qquad}}<math>C_{13} = C_{31}  = C_{42} = C_{24}\,</math>{{qquad}}<math>C_{14} = C_{41}\,</math>{{qquad}}{{qquad}}<math>C_{23} = C_{32}\,</math></center>
	lo que nos reduce la matriz de coeficientes de capacidad a		lo que nos reduce la matriz de coeficientes de capacidad a
-	\mathbf{\mathsf{C}}=\begin{pmatrix}C_{11} & C_{12} & C_{13} & C_{14}\\ C_{12} & C_{22} & C_{23} & C_{13}\\ C_{13} & C_{23} & C_{22} & C_{12} \\ C_{14} &C_{13} & C_{12} & C_{11}\end{pmatrix}	+	<center><math>
		+	\mathbf{\mathsf{C}}=\begin{pmatrix}C_{11} & C_{12} & C_{13} & C_{14}\\ C_{12} & C_{22} & C_{23} & C_{13}\\ C_{13} & C_{23} & C_{22} & C_{12} \\ C_{14} &C_{13} & C_{12} & C_{11}\end{pmatrix}</math></center>
		+
		+	==Apantallamiento==
		+	De entre estos coeficientes, serán nulos aquellos que relacionen dos conductores apantallados por un tercero. Por ello,
		+
		+	<center><math>C_{13} = C_{14} = C_{24} = 0\,</math></center>
		+
		+	Además, dado que el conductor 1 está en posición de influencia total respecto al 2, se cumple la relación
		+
		+	<center><math>C_{12}=-C_{11}\,</math></center>
		+
		+	quedando pues que toda la matriz puede expresarse en términos de tres coeficientes
		+
		+	<center><math>\mathbf{\mathsf{C}}=\begin{pmatrix}C_{11} & -C_{11} & 0 & 0\\ -C_{11} & C_{22} & C_{23}
		+	& 0\\ 0 & C_{23} & C_{22} & -C_{11} \\ 0 & 0 & -C_{11} & C_{11}\end{pmatrix}</math></center>
		+
		+	==Signos==
		+	De los coeficientes que quedan, serán positivos aquellos que relacionen a un conductor consigo mismo
		+
		+	<center><math>C_{11}>0\,</math>{{qquad}}{{qquad}}<math>C_{22}>0\,</math></center>
-	De entre estos coeficientes, serán nulos aquellos que relacionen dos
-	conductores apantallados por un tercero. Por ello,
-	\[
-	C_{13} = C_{14} = C_{24} = 0
-	\]
-	Además, dado que el conductor 1 está en posición de influencia total
-	respecto al 2, se cumple la relación
-	\[
-	C_{12}=-C_{11}
-	\]
-	quedando pues que toda la matriz puede expresarse en términos de tres
-	coeficientes
-	\[
-	\mathbf{\mathsf{C}=\pmatrix{C_{11} & -C_{11} & 0 & 0\cr -C_{11} & C_{22} & C_{23}
-	& 0\cr 0 & C_{23} & C_{22} & -C_{11} \cr 0 & 0 & -C_{11} & C_{11}}
-	\]
-	De los coeficientes que quedan, serán positivos aquellos que relacionen
-	a un conductor consigo mismo
-	\[
-	C_{11}>0\qquad C_{22}>0
-	\]
	Serán negativos aquellos que relacionen a un conductor con los demás.		Serán negativos aquellos que relacionen a un conductor con los demás.
-	\[
-	C_{12}<0\qquad C_{23}<0
-	\]
-	\indent Cuando se unen los conductores por hilos ideales pasamos a
-	tener un sistema de sólo dos conductores, también simétrico. El
-	conductor 1' es la unión del 1 y del 3, mientras que el 2' une al 2 con
-	el 4. Estas relaciones se pueden expresar matemáticamente por
-	\[
-	Q_{1'}=Q_{1}+Q_{3}\qquad V_{1'}=V_{1}=V_3
-	\qquad
-	Q_{2'}=Q_2+Q_4\qquad V_{2'}=V_2=V_4
-	\]
-	Sustituyendo las relaciones entre las cargas y los potenciales en el
-	sistema original resulta
-	\[
-	C_{1'1'}=C_{2'2'}=C_{11}+C_{22}\qquad C_{1'2'}=C_{2'1'}=2C_{12}+C_{23}
-	\]
-	donde se ha tenido en cuenta que algunos coeficientes se anulan y otros
-	son iguales entre sí.
-	Una forma alternativa y más directa de obtener la nueva matriz de	+	<center><math>C_{12}<0\,</math>{{qquad}}{{qquad}}<math>C_{23}<0\,</math></center>
-	coeficientes de capacidad es por métodos matriciales. Para representar	+
-	las conexiones, introducimos una matriz $\mathbf{\mathsf{T}$, obtenida	+	==Conexiones==
-	a partir de la matriz identidad, uniendo las filas de aquellos	+	===Empleando las cargas y tensiones===
-	conductores que se conectan. En nuestro caso, en que se conectan el 1	+	Cuando se unen los conductores por hilos ideales pasamos a tener un sistema de sólo dos conductores, también simétrico. El conductor 1' es la unión del 1 y del 3, mientras que el 2' une al 2 con el 4. Estas relaciones se pueden expresar matemáticamente por
-	con el 3 para formar el 1', y los dos restantes para construir el 2',	+
-	esta matriz sería	+	<center><math>Q_{1'}=Q_{1}+Q_{3}\,</math>{{qquad}} <math>V_{1'}=V_{1}=V_3\,</math>{{qquad}}{{qquad}}{{qquad}}<math>Q_{2'}=Q_2+Q_4\,</math>{{qquad}}{{qquad}}<math>V_{2'}=V_2=V_4\,</math></center>
-	\[	+
-	\mathbf{\mathsf{T}=\pmatrix{1 & 0 & 1 & 0 \cr 0 & 1 & 0 & 1}	+	Sustituyendo las relaciones entre las cargas y los potenciales en el sistema original resulta
-	\]	+
-	Definida esta matriz (que será diferente en cada problema, dependiendo	+	<center><math>C_{1'1'}=C_{2'2'}=C_{11}+C_{22}\,</math>{{qquad}}<math>C_{1'2'}=C_{2'1'}=2C_{12}+C_{23}\,</math></center>
-	de las conexiones que se efectúen), la nueva matriz de coeficientes de	+
-	capacidad se calcula como	+	donde se ha tenido en cuenta que algunos coeficientes se anulan y otros son iguales entre sí.
-	\[	+
-	\mathbf{\mathsf{C}'=\mathbf{\mathsf{T}\cdot\mathbf{\mathsf{C}\cdot\mathbf{\mathsf{T}^t	+	===Usando álgebra matricial===
-	\]	+	Una forma alternativa y más directa de obtener la nueva matriz de coeficientes de capacidad es por métodos matriciales. Para representar
		+	las conexiones, introducimos una matriz <math>\mathbf{\mathsf{T}}</math>, obtenida a partir de la matriz identidad, uniendo las filas de aquellos conductores que se conectan. En nuestro caso, en que se conectan el 1 con el 3 para formar el 1', y los dos restantes para construir el 2', esta matriz sería
		+
		+	<center><math>\mathbf{\mathsf{T}}=\begin{pmatrix}1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1\end{pmatrix}</math></center>
		+
		+	Definida esta matriz (que será diferente en cada problema, dependiendo de las conexiones que se efectúen), la nueva matriz de coeficientes de capacidad se calcula como
		+
		+	<center><math>\mathbf{\mathsf{C}}'=\mathbf{\mathsf{T}}\cdot\mathbf{\mathsf{C}}\cdot\mathbf{\mathsf{T}}^t</math></center>
		+
	En nuestro caso		En nuestro caso
-	\[
-	\mathbf{\mathsf{C'}=\pmatrix{1 & 0 & 1 & 0 \cr 0 & 1 & 0 & 1}{\cdot}
-	\pmatrix{C_{11} & -C_{11} & 0 & 0\cr -C_{11} & C_{22} & C_{23}
-	& 0\cr 0 & C_{23} & C_{22} & -C_{11} \cr 0 & 0 & -C_{11} & C_{11}}{\cdot}
-	\pmatrix{1 & 0 \cr 0 & 1 \cr 1 & 0 \cr 0 & 1} =
-	%\]\[=
-	\pmatrix{C_{11}+C_{22} & -2C_{11}+C_{23} \cr -2C_{11}+C_{23} &
-	C_{11}+C_{22}}
-	\]
-	%\dibujops{cap2-03}
-	Una tercera forma de resolver el problema es usando
-	un circuito equivalente. Vemos que el sistema puede sustituirse por
-	cinco condensadores: dos idénticos $\overline{C}_{12}$, que unen el
-	conductor 1 con el 2 y el 3 con el 4, respectivamente: otros dos de
-	valor $\overline{C}_{22}$ que unen el 2 con tierra y el 3 con tierra; y
-	el último, $\overline{C}_{23}$, que une el conductor 2 con el 3. A
-	partir de estas capacidades resultan los coeficientes de capacidad
-	\[
-	C_{11}=\overline{C}_{12} \qquad C_{12}=-\overline{C}_{12}
-	\]
-	%\dibujops{cap2-04}
-	\[
-	C_{22}=\overline{C}_{12}+\overline{C}_{22}+\overline{C}_{23}
-	\qquad
-	C_{23}=-\overline{C}_{23}
-	\]
-	\begin{center}
-	\includegr{cap2-03.eps}\hspace{1cm}\includegr{cap2-04.eps}
-	\end{center}
-	Las uniones 1--3 y 2--4 reducen el sistema mediante la asociación en
-	paralelo de tres de los cinco condensadores, obteniéndose las nuevas
-	capacidades simplemente sumando, y a partir de éstas, los nuevos
-	coeficientes de capacidad.
-	%\vspace*{1cm}
-	\end{solucion}	+	<center><math>\mathbf{\mathsf{C'}}=\begin{pmatrix}1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1\end{pmatrix}{\cdot}
		+	\begin{pmatrix}C_{11} & -C_{11} & 0 & 0\\ -C_{11} & C_{22} & C_{23}
		+	& 0\\ 0 & C_{23} & C_{22} & -C_{11} \\ 0 & 0 & -C_{11} & C_{11}\end{pmatrix}{\cdot}
		+	\begin{pmatrix}1 & 0 \\ 0 & 1 \\ 1 & 0 \\ 0 & 1\end{pmatrix} =  \begin{pmatrix}C_{11}+C_{22} & -2C_{11}+C_{23} \\ -2C_{11}+C_{23} &
		+	C_{11}+C_{22}\end{pmatrix}</math></center>
		+
		+	===Mediante un circuito equivalente===
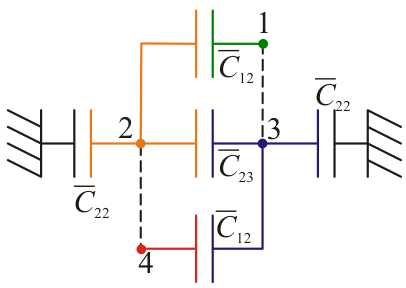
		+	[[Imagen:circuito4conductores1.png|left]]Una tercera forma de resolver el problema es usando un circuito equivalente. Vemos que el sistema puede sustituirse por cinco condensadores: dos idénticos <math>\overline{C}_{12}</math>, que unen el conductor 1 con el 2 y el 3 con el 4, respectivamente: otros dos de valor <math>\overline{C}_{22}</math> que unen el 2 con tierra y el 3 con tierra; y el último, <math>\overline{C}_{23}</math>, que une el conductor 2 con el 3. A partir de estas capacidades resultan los coeficientes de capacidad
		+
		+	<center><math>C_{11}=\overline{C}_{12}</math>{{qquad}}{{qquad}}<math>C_{12}=-\overline{C}_{12}</math>{{qquad}}{{qquad}}<math>C_{22}=\overline{C}_{12}+\overline{C}_{22}+\overline{C}_{23}</math>{{qquad}}{{qquad}}<math>C_{23}=-\overline{C}_{23}</math></center>
		+
		+	Las uniones 1&mdash;3 y 2&mdash;4 reducen el sistema mediante la asociación en paralelo de tres de los cinco condensadores, obteniéndose las nuevas capacidades simplemente sumando,
		+
		+	<center><math>\overline{C}_{1'1'} = \overline{C}_{2'2'}=\overline{C}_{22}</math>{{qquad}}{{qquad}}<math>\overline{C}_{1'2'}=2\overline{C}_{12}+\overline{C}_{23}</math>{{qquad}}{{qquad}}</center>
		+
		+	y, conocidas las capacidades y autocapacidades hallamos los coeficientes de capacidad e inducción
		+
		+	<center>[[Imagen:circuito4conductores2.png]]{{qquad}}[[Imagen:circuito4conductores3.png]]</center>
		+
		+	<center><math>C_{1'1'}=C_{2'2'}= \overline{C}_{1'1'} = \overline{C}_{22}+2\overline{C}_{12}+\overline{C}_{23}</math>{{qquad}}{{qquad}}<math>C_{1'2'}=-\overline{C}_{1'2'}=-2\overline{C}_{12}-\overline{C}_{23}</math></center>
		+
		+	Sustituyendo ahora las capacidades en función de los coeficientes de capacidad originales
		+	<center>
		+	<math>C_{1'1'} = (C_{12}+C_{22}+C_{23})+2(-C_{12})+(-C_{23}) = C_{22}-C_{12}=C_{11}+C_{22}\,</math>{{qquad}}{{qquad}}
		+	<math>C_{1'2'}=-\overline{C}_{1'2'}=-2\overline{C}_{12}-\overline{C}_{23}= 2C_{12}+C_{23}</math></center>
-	[[Categoría:Problemas de campo eléctrico en presencia de conductores]]	+	[[Categoría:Problemas de electrostática en presencia de conductores]]

---

última version al 20:40 10 ene 2010

Contenido 1 Enunciado 2 Introducción 3 Simetría 1–4 y 2–3 4 Apantallamiento 5 Signos 6 Conexiones 6.1 Empleando las cargas y tensiones 6.2 Usando álgebra matricial 6.3 Mediante un circuito equivalente

1 Enunciado

Considere el sistema de cuatro conductores de la figura. Está formado por cuatro superficies esféricas situadas dos dentro de las otras dos (no concéntricamente). En este sistema, los conductores 1 y el 2 son simétricos con el 4 y el 3, respectivamente.

Para este sistema, ¿qué coeficientes de capacidad e inducción son nulos? ¿Cuáles positivos? ¿Cuáles negativos? ¿Cuáles iguales entre sí?

Suponga que mediante finos hilos conductores se conecta el conductor 1 con el 3, y el 2 con el 4 (estos cables atraviesan, sin hacer contacto, los conductores 2 y 3). ¿Cómo queda la nueva matriz de capacidades a partir de la matriz del sistema original?

2 Introducción

En este problema no se trata de establecer los valores exactos de los coeficientes, sino algunas de sus propiedades. Por ello, la geometría exacta es menos importante que la topología del problema, esto es, qué conductores están contenidos por cuáles.

3 Simetría 1–4 y 2–3

Dada la simetría especular del sistema, lo más inmediato es determinar cuáles de los coeficientes de capacidad son iguales entre sí. De entrada, la matriz de coeficientes de capacidad es simétrica. Los coeficientes serán iguales si hacemos la permutación 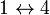y 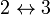. Obtenemos las siguientes equivalencias

                                    

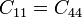
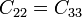
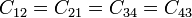
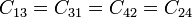
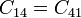
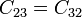
lo que nos reduce la matriz de coeficientes de capacidad a

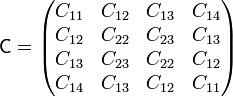
4 Apantallamiento

De entre estos coeficientes, serán nulos aquellos que relacionen dos conductores apantallados por un tercero. Por ello,

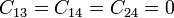
Además, dado que el conductor 1 está en posición de influencia total respecto al 2, se cumple la relación

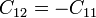
quedando pues que toda la matriz puede expresarse en términos de tres coeficientes

5 Signos

De los coeficientes que quedan, serán positivos aquellos que relacionen a un conductor consigo mismo

        

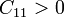
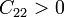
Serán negativos aquellos que relacionen a un conductor con los demás.

        

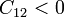
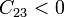
6 Conexiones

6.1 Empleando las cargas y tensiones

Cuando se unen los conductores por hilos ideales pasamos a tener un sistema de sólo dos conductores, también simétrico. El conductor 1' es la unión del 1 y del 3, mientras que el 2' une al 2 con el 4. Estas relaciones se pueden expresar matemáticamente por

                         

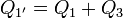
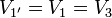
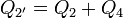
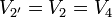
Sustituyendo las relaciones entre las cargas y los potenciales en el sistema original resulta

    

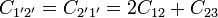
donde se ha tenido en cuenta que algunos coeficientes se anulan y otros son iguales entre sí.

6.2 Usando álgebra matricial

Una forma alternativa y más directa de obtener la nueva matriz de coeficientes de capacidad es por métodos matriciales. Para representar las conexiones, introducimos una matriz 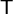, obtenida a partir de la matriz identidad, uniendo las filas de aquellos conductores que se conectan. En nuestro caso, en que se conectan el 1 con el 3 para formar el 1', y los dos restantes para construir el 2', esta matriz sería

Definida esta matriz (que será diferente en cada problema, dependiendo de las conexiones que se efectúen), la nueva matriz de coeficientes de capacidad se calcula como

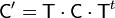
En nuestro caso

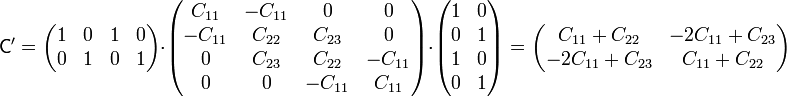
6.3 Mediante un circuito equivalente

Una tercera forma de resolver el problema es usando un circuito equivalente. Vemos que el sistema puede sustituirse por cinco condensadores: dos idénticos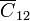 , que unen el conductor 1 con el 2 y el 3 con el 4, respectivamente: otros dos de valor 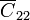que unen el 2 con tierra y el 3 con tierra; y el último, 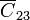, que une el conductor 2 con el 3. A partir de estas capacidades resultan los coeficientes de capacidad                         

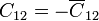
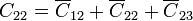
Las uniones 1—3 y 2—4 reducen el sistema mediante la asociación en paralelo de tres de los cinco condensadores, obteniéndose las nuevas capacidades simplemente sumando,

                

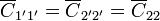
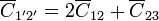
y, conocidas las capacidades y autocapacidades hallamos los coeficientes de capacidad e inducción

             

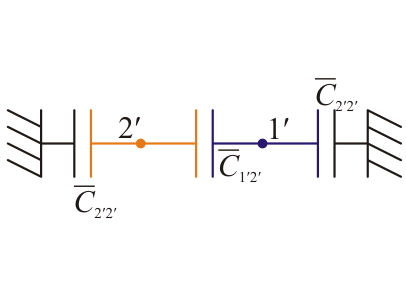
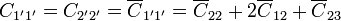
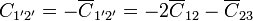
Sustituyendo ahora las capacidades en función de los coeficientes de capacidad originales