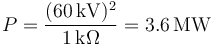Dos esferas conductoras dentro de otra

De Laplace

(Diferencias entre revisiones)

última version al 11:16 8 jul 2014

Contenido

1 Enunciado
2 Potenciales antes de la conexión
3 Estado tras la conexión
4 Cambio en la energía almacenada
5 Potencia disipada

1 Enunciado

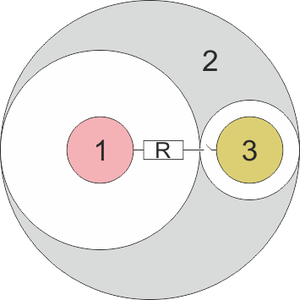
Se tiene un sistema de tres conductores esféricos. Uno de ellos (“2”) es una esfera de radio 54 mm con dos huecos esféricos, de radios 36 mm y 18 mm. En el centro de cada hueco se encuentran sendas esferas metálicas de radio 12 mm, siendo “1” la que está en el hueco grande y “3” la que está en el pequeño. Entre las esferas hay vacío y no hay más conductores ni cargas en el sistema.

Inicialmente la esfera “1” contiene una carga 120 nC mientras que los otros dos conductores están aislados y descargados.

Halle el potencial de cada conductor, así como la energía almacenada en el sistema.
Se conectan las dos esferas interiores mediante un hilo de resistencia 1 kΩ. Una vez que se ha vuelto a alcanzar el estado final, ¿cuáles son los nuevos potenciales de los conductores?
¿Cuál es la nueva energía almacenada? ¿Cuánta energía se ha disipado en la resistencia?
Halle la potencia instantánea disipada en el cable justo tras la conexión.

Tómese

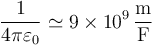
$\frac{1}{4\pi\varepsilon_0}\simeq 9\times 10^9\,\frac{\mathrm{m}}{\mathrm{F}}$

2 Potenciales antes de la conexión

La forma más sencilla de resolver este problema es mediante la construcción de un circuito equivalente.

En este caso, tenemos tres condensadores:

Uno esférico entre la esfera 1 y la pared del hueco de 2, de capacidad

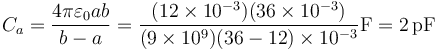
$C_a=\frac{4\pi\varepsilon_0 a b}{b-a}=\frac{(12\times 10^{-3})(36\times 10^{-3})}{(9\times 10^9)(36-12)\times 10^{-3}}\mathrm{F}=2\,\mathrm{pF}$

Otro esférico entre la esfera 3 y la pared del hueco de 2, de capacidad

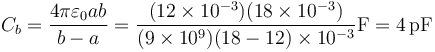
$C_b=\frac{4\pi\varepsilon_0 a b}{b-a}=\frac{(12\times 10^{-3})(18\times 10^{-3})}{(9\times 10^9)(18-12)\times 10^{-3}}\mathrm{F}=4\,\mathrm{pF}$

Uno entre la superficie exterior del conductor 2 y el infinito, que se puede calcular a partir de la capacidad de un conductor esférico o de un condensador esférico con $b\to\infty$

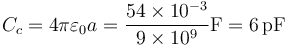
$C_c=4\pi\varepsilon_0a =\frac{54\times 10^{-3}}{9\times 10^9}\mathrm{F}=6\,\mathrm{pF}$

No hay más condensadores en el circuito equivalente. Aparte, habrá que colocar una resistencia entre los nodos 1 y 3, aunque en este primer apartado no es necesaria.

Una vez que tenemos las capacidades, podemos relacionar las cargas en cada conductor con los voltajes, sumando la carga de condensador conectado a cada nodo

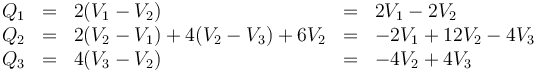
$\begin{array}{rclcl} Q_1& = & 2(V_1-V_2) & = & 2V_1-2V_2\\ Q_2 & = & 2(V_2-V_1)+4(V_2-V_3)+6V_2& = &-2V_1+12V_2-4V_3 \\ Q_3 & = & 4(V_3-V_2) & = & -4V_2+4V_3 \end{array}$

donde hemos medido la carga en nC, el voltaje en kV y la capacidad en pF 8de esta forma resultan cantidades sin exponentes).

A estas ecuaciones debemos añadir 3 más que completen el sistema. En este caso es que conocemos la carga de los tres conductores

$Q_1=Q_0=120\,\mathrm{nC}\qquad Q_2=0\qquad Q_3 = 0$

Llevando esto al sistema de arriba obtenemos el sistema de tres ecuaciones con tres incógnitas

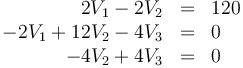
$\begin{array}{rcl} 2V_1-2V_2 & = &120\\ -2V_1+12V_2-4V_3 & = & 0\\ -4V_2+4V_3 & = & 0 \end{array}$

que tiene por solución

$V_1= 80\,\mathrm{kV} \qquad\qquad V_2=V_3=20\,\mathrm{kV}$

Alternativamente, podemos resolverlo analizando exclusivamente el circuito equivalente. Inicialmente tenemos que el conductor 3 no está cargado, por lo que la carga del condensador $C b$ es nula y no hay diferencia de potencial entre sus placas, es decir

$V_2 = V_3\,$

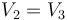
En términos electromagnéticos, lo que ocurre es que por el teorema de Faraday, si no hay carga en el interior del hueco, no hay campo en ese hueco.

El conductor 1 sí está cargado, con 120 nC, por lo que

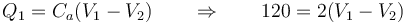
$Q_1=C_a(V_1-V_2)\qquad\Rightarrow\qquad 120 = 2(V_1-V_2)$

donde la carga se mide en nC, la capacidad en pF y el voltaje en kV.

El conductor 2 está descargado, por lo que

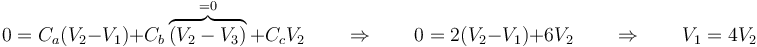
$0 = C_a(V_2-V_1) + C_b\overbrace{(V_2-V_3)}^{=0}+C_cV_2\qquad\Rightarrow\qquad 0=2(V_2-V_1)+6V_2\qquad \Rightarrow\qquad V_1=4V_2$

y llevando esto a la relación de arriba queda

$V_1 = 80\,\mathrm{kV}\qquad\qquad V_2=V_3=20\,\mathrm{kV}$

De otra forma, podemos ver que en este caso el sistema se reduce a solo dos condensadores puestos en serie (pues el b, es como si no estuviera), siendo la capacidad equivalente

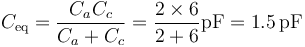
$C_\mathrm{eq}=\frac{C_aC_c}{C_a+C_c}=\frac{2\times 6}{2+6}\mathrm{pF}=1.5\,\mathrm{pF}$

y conociendo la capacidad obtenemos el potencial del conductor 1

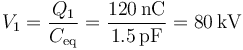
$V_1=\frac{Q_1}{C_\mathrm{eq}}=\frac{120\,\mathrm{nC}}{1.5\,\mathrm{pF}}=80\,\mathrm{kV}$

y puesto que los dos conductores están en serie, la carga del condensador $C c$ , lo que nos da el potencial del conductor 2 (y del 3)

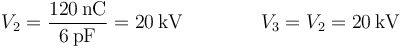
$V_2=\frac{120\,\mathrm{nC}}{6\,\mathrm{pF}}=20\,\mathrm{kV}\qquad\qquad V_3=V_2=20\,\mathrm{kV}$

Una vez que tenemos las cargas y potenciales de los tres conductores es inmediato el cálculo de la energía almacenada

$U_\mathrm{e}=\frac{1}{2}Q_1V_1+\frac{1}{2}\overbrace{Q_2}^{=0}V_2+\frac{1}{2}\overbrace{Q_3}^{=0}V_3=\frac{1}{2}(120\,\mathrm{nC})(80\,\mathrm{kV})=4800\,\mu\mathrm{J}$

También podemos hallar esta energía sumando la almacenada en cada condensador

$U_\mathrm{e}=\frac{1}{2}C_a(V_1-V_2)^2+\frac{1}{2}C_b(V_3-V_2)^2+\frac{1}{2}C_cV_2^2=\left(\frac{1}{2}2(80-20)^2+\frac{1}{2}4(20-20)^2+\frac{1}{2}6\times 20^2\right)\mu\mathrm{J}=4800\,\mu\mathrm{J}$

o directamente con la capacidad equivalente

$U_\mathrm{e}=\frac{Q_1^2}{2C_\mathrm{eq}}=\frac{120^2}{2\times 1.5}\mu\mathrm{J}=4800\,\mu\mathrm{J}$

3 Estado tras la conexión

Cuando se cierra el interruptor, comienza a fluir una corriente desde el conductor a más potencial (el 1) al de menos (el 3), reduciéndose el voltaje del primero y aumentando el del segundo. El proceso cesa cuando se igualan los potenciales. En el nuevo estado de equilibrio

$V'_1=V'_3\,$

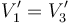
Volviendo al sistema de ecuuaciones se trataría de completar el sistema

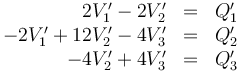
$\begin{array}{rcl} 2V'_1-2V'_2 & = & Q'_1\\ -2V'_1+12V'_2-4V'_3 & = & Q'_2\\ -4V'_2+4V'_3 & = & Q'_3 \end{array}$

con las tres ecuaciones

$Q'_1+Q'_3 = 120\,\mathrm{nC}\qquad\qquad Q'_2=0\qquad\qquad V'_1=V'_3$

Despejando y sustituyendo, obtenemos la solución para los potenciales

$V'_1=V'_3=40\,\mathrm{kV}\qquad \qquad V'_2=20\,\mathrm{kV}$

Vemos que el voltaje del conductor 1 se ha reducido a la mitad del que tenía, mientras que el del 3 ha aumentado al doble. Para las cargas

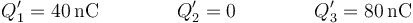
$Q'_1=40\,\mathrm{nC}\qquad\qquad Q'_2=0\qquad\qquad Q'_3=80\,\mathrm{nC}$

Podemos resolverlo empleando exclusivamente el circuito equivalente. En éste, los condensadores $C a$ y $C b$ están en paralelo, siendo la capacidad equivalente a estos dos

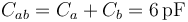
$C_{ab}=C_a+C_b=6\,\mathrm{pF}$

y la total del sistema

$C'_\mathrm{eq}=\frac{C_{ab}C_c}{C_{ab}+C_c}=\frac{6\times 6}{6+6}\mathrm{pF}=3\,\mathrm{pF}$

Esto nos da el nuevo voltaje del conductor 1 (y del 3)

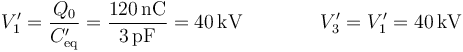
$V'_1=\frac{Q_0}{C'_\mathrm{eq}}=\frac{120\,\mathrm{nC}}{3\,\mathrm{pF}}=40\,\mathrm{kV}\qquad\qquad V'_3=V'_1=40\,\mathrm{kV}$

El voltaje del conductor 2, en cambio, no se ve modificado

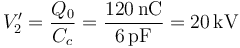
$V'_2=\frac{Q_0}{C_c}=\frac{120\,\mathrm{nC}}{6\,\mathrm{pF}}=20\,\mathrm{kV}$

Una vez que tenemos la diferencia de potencial podemos hallar la carga de cada conductor

$Q'_1=C_a(V'_1-V'_2) = 2(40-20)\,\mathrm{nC}=40\,\mathrm{nC}\qquad\qquad Q'_3=C_a(V'_3-V'_2) = 4(40-20)\,\mathrm{nC}=80\,\mathrm{nC}$

4 Cambio en la energía almacenada

La energía almacenada en el estado final se calcula como la inicial, siendo ahora

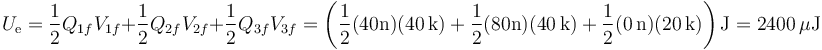
$U_\mathrm{e}=\frac{1}{2}Q_{1f}V_{1f}+\frac{1}{2}Q_{2f}V_{2f}+\frac{1}{2}Q_{3f}V_{3f}=\left(\frac{1}{2}(40\mathrm{n})(40\,\mathrm{k})+\frac{1}{2}(80\mathrm{n})(40\,\mathrm{k})+\frac{1}{2}(0\,\mathrm{n})(20\,\mathrm{k})\right)\mathrm{J}=2400\,\mu\mathrm{J}$

Lo que nos da una disipación de energía

$\Delta U_\mathrm{e} =U_{\mathrm{e}f}-U_{\mathrm{e}i}=2400\,\mu\mathrm{J}$

5 Potencia disipada

La potencia disipada en el instante inicial la obtenemos mediante la ley de Joule

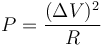
$P=\frac{(\Delta V)^2}{R}$

siendo $Δ V$ la diferencia de potencial entre los extremos de la resistencia, que son los conductores 1 y 3. Por tanto

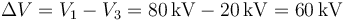
$\Delta V = V_1-V_3=80\,\mathrm{kV}-20\,\mathrm{kV}=60\,\mathrm{kV}$

y por tanto

$P = \frac{(60\,\mathrm{kV})^2}{1\,\mathrm{k}\Omega}=3.6\,\mathrm{MW}$

@@ Línea 156: / Línea 156: @@
 Lo que nos da una disipación de energía
-<center><math>\Delta U_\mathrm{e} =U_{\mathrm{e}f}-U_\mathrm{e}i}=2400\,\mu\mathrm{J}</math></center>
+<center><math>\Delta U_\mathrm{e} =U_{\mathrm{e}f}-U_{\mathrm{e}i}=2400\,\mu\mathrm{J}</math></center>
 ==Potencia disipada==
+La potencia disipada en el instante inicial la obtenemos mediante la ley de Joule
+<center><math>P=\frac{(\Delta V)^2}{R}</math></center>
+siendo <math>\Delta V</math> la diferencia de potencial entre los extremos de la resistencia, que son los conductores 1 y 3. Por tanto
+<center><math>\Delta V = V_1-V_3=80\,\mathrm{kV}-20\,\mathrm{kV}=60\,\mathrm{kV}</math></center>
+y por tanto
+<center><math>P = \frac{(60\,\mathrm{kV})^2}{1\,\mathrm{k}\Omega}=3.6\,\mathrm{MW}</math></center>
 [[Categoría:Problemas de electrostática en medios materiales (GIE)]]

Dos esferas conductoras dentro de otra

De Laplace

última version al 11:16 8 jul 2014

Contenido

1 Enunciado

2 Potenciales antes de la conexión

3 Estado tras la conexión

4 Cambio en la energía almacenada

5 Potencia disipada

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES