Cálculo de eficiencias máximas
De Laplace
(→Máquinas térmicas) |
(→Bombas de calor) |
||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 38: | Línea 38: | ||
En el caso de un refrigerador, el equivalente al rendimiento es el coeficiente de desempeño, que para un refrigerador que funcione mediante un ciclo reversible vale | En el caso de un refrigerador, el equivalente al rendimiento es el coeficiente de desempeño, que para un refrigerador que funcione mediante un ciclo reversible vale | ||
| - | <center><math>\mathrm{COP}_R = \frac{Q_\mathrm{in}}{W_\mathrm{in}}=\frac{T_F}{T_C-T_F}</math></center> | + | <center><math>\mathrm{COP}_R^\mathrm{rev} = \frac{Q_\mathrm{in}}{W_\mathrm{in}}=\frac{T_F}{T_C-T_F}</math></center> |
Con esta fórmula, el valor máximo pedido es | Con esta fórmula, el valor máximo pedido es | ||
;Entre 4°C y 25°C: | ;Entre 4°C y 25°C: | ||
| - | <center><math>\mathrm{COP}_R = \frac{275}{21}=13.1</math></center> | + | <center><math>\mathrm{COP}_R^\mathrm{rev} = \frac{275}{21}=13.1</math></center> |
;Entre 0°C y 100°C: | ;Entre 0°C y 100°C: | ||
| - | <center><math>\mathrm{COP}_R = \frac{273}{100}=2.73</math></center> | + | <center><math>\mathrm{COP}_R^\mathrm{rev} = \frac{273}{100}=2.73</math></center> |
Observemos que mientras el rendimiento de una máquina térmica aumenta al crecer la diferencia de temperaturas, el coeficiente de desempeño disminuye, ya que cuanto mayor sea la diferencia de temperaturas que hay que superar, más trabajo se necesita para conseguirlo. | Observemos que mientras el rendimiento de una máquina térmica aumenta al crecer la diferencia de temperaturas, el coeficiente de desempeño disminuye, ya que cuanto mayor sea la diferencia de temperaturas que hay que superar, más trabajo se necesita para conseguirlo. | ||
| Línea 51: | Línea 51: | ||
El coeficiente de desempeño de una bomba de calor es parecido al de refrigerador solo que se considera el calor expulsado, en vez del absorbido. Para uno reversible | El coeficiente de desempeño de una bomba de calor es parecido al de refrigerador solo que se considera el calor expulsado, en vez del absorbido. Para uno reversible | ||
| - | <center><math>\mathrm{COP}_{BC} = \frac{Q_\mathrm{out}}{W_\mathrm{in}}=\frac{T_C}{T_C-T_F}</math></center> | + | <center><math>\mathrm{COP}^\mathrm{rev}_{BC} = \frac{Q_\mathrm{out}}{W_\mathrm{in}}=\frac{T_C}{T_C-T_F}</math></center> |
Se cumple la relación entre los dos coeficientes de desempeño: | Se cumple la relación entre los dos coeficientes de desempeño: | ||
| - | <center><math>\mathrm{COP}_{BC}=\mathrm{COP}_R+1\,</math></center> | + | <center><math>\mathrm{COP}^\mathrm{rev}_{BC}=\mathrm{COP}^\mathrm{rev}_R+1\,</math></center> |
lo que nos da los valores | lo que nos da los valores | ||
;Entre 4°C y 25°C: | ;Entre 4°C y 25°C: | ||
| - | <center><math>\mathrm{COP}_{BC} = \frac{298}{21}=1.0+13.1=14.1</math></center> | + | <center><math>\mathrm{COP}^\mathrm{rev}_{BC} = \frac{298}{21}=1.0+13.1=14.1</math></center> |
;Entre 0°C y 100°C: | ;Entre 0°C y 100°C: | ||
| - | <center><math>\mathrm{COP}_{BC} = \frac{373}{100}=3.73</math></center> | + | <center><math>\mathrm{COP}^\mathrm{rev}_{BC} = \frac{373}{100}=3.73</math></center> |
[[Categoría:Problemas del segundo principio de la termodinámica (GIE)]] | [[Categoría:Problemas del segundo principio de la termodinámica (GIE)]] | ||
última version al 18:15 3 abr 2014
Contenido |
1 Enunciado
Calcule el rendimiento máximo que puede tener una máquina térmica que funcione entre
- 0°C y 100°C.
- 100°C y 200°C.
- 27°C y 1200 K.
Halle asimismo el coeficiente de desempeño máximo que pueden tener un refrigerador que funcione entre
- 4°C y 25°C.
- 0°C y 100°C.
Calcule igualmente los valores máximos del coeficiente de desempeño para una bomba de calor que funcione entre las temperaturas de los dos apartados anteriores.
2 Máquinas térmicas
El rendimiento máximo de una máquina térmica lo da el de una máquina reversible que opere entre las dos temperaturas indicadas, absorbiendo calor a la temperatura más alta y cediéndolo a la más baja. El rendimiento de una máquina reversible es
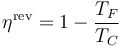
donde TF y TC son las temperaturas absolutas del foco frío y del foco caliente, respectivamente. Con esta fórmula obtenemos los rendimientos máximos
- Entre 0°C y 100°C
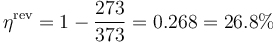
- Entre 100°C y 200°C
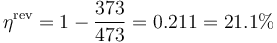
- Vemos que igual diferencia de temperaturas no implica igualdad de rendimiento, sino que depende de las temperaturas absolutas de los focos.
- Entre 27°C y 1200 K
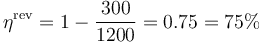
De esta fórmula se deduce que las únicas formas de aumentar el rendimiento máximo son:
- Reduciendo la temperatura del foco frío.
- Aumentando la temperatura del foco caliente.
3 Refrigeradores
En el caso de un refrigerador, el equivalente al rendimiento es el coeficiente de desempeño, que para un refrigerador que funcione mediante un ciclo reversible vale
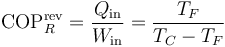
Con esta fórmula, el valor máximo pedido es
- Entre 4°C y 25°C
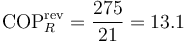
- Entre 0°C y 100°C
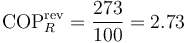
Observemos que mientras el rendimiento de una máquina térmica aumenta al crecer la diferencia de temperaturas, el coeficiente de desempeño disminuye, ya que cuanto mayor sea la diferencia de temperaturas que hay que superar, más trabajo se necesita para conseguirlo.
4 Bombas de calor
El coeficiente de desempeño de una bomba de calor es parecido al de refrigerador solo que se considera el calor expulsado, en vez del absorbido. Para uno reversible
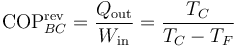
Se cumple la relación entre los dos coeficientes de desempeño:
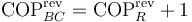
lo que nos da los valores
- Entre 4°C y 25°C
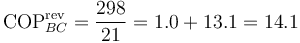
- Entre 0°C y 100°C






