Masa que cae sobre resorte

De Laplace

(Diferencias entre revisiones)

última version al 19:09 28 ene 2014

Contenido

1 Enunciado
2 Compresión del resorte
3 Velocidad de impacto
4 Nueva altura máxima
5 Máxima compresión
6 Energía disipada
7 Máxima compresión en el caso inelástico

1 Enunciado

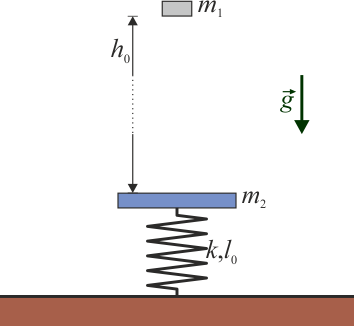
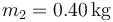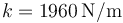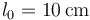Se tiene una plataforma de masa $m_2=0.40\,\mathrm{kg}$ situada sobre un resorte de constante $k=1960\,\mathrm{N}/\mathrm{m}$ y longitud natural $l_0=10\,\mathrm{cm}$ .

Calcule cuánto se comprime el resorte debido al peso de la masa, en la posición de equilibrio.

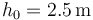Sobre esta plataforma se deja caer una masa $m_1= 0.10\,\mathrm{kg}$ , soltándola sin velocidad inicial desde una altura $h_0= 2.5\,\mathrm{m}$ sobre la plataforma

Calcule la velocidad que tiene la masa $m 1$ justo antes de impactar con la plataforma.

Si la colisión es perfectamente elástica,

Calcule la nueva altura que alcanza la masa $m 1$ tras la colisión.
Calcule cuánto es el máximo que se comprime el resorte por efecto del golpe en la plataforma.

Si la colisión, en vez de ser elástica, es completamente inelástica,

¿Cuánta energía se pierde en la colisión?
¿Cuánto se comprime como máximo el resorte tras la colisión?

Tómese 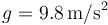$g=9.8\,\mathrm{m}/\mathrm{s}^2$ .

2 Compresión del resorte

Puesto que todas las fuerzas y velocidades van a ser verticales, el problema es unidimensional y podemos emplear cantidades escalares con signo. Consideraremos una velocidad y una fuerza como positivas cuando van hacia abajo y negativas si van hacia arriba.

La presencia de la masa comprime el muelle por acción de su peso. En el equilibrio se compensa la acción del peso con la fuerza recuperadora elástica:

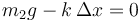
$m_2g-k\,\Delta x=0$

lo que da la compresión del muelle

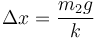
$\Delta x = \frac{m_2g}{k}$

Sustituyendo los valores numéricos

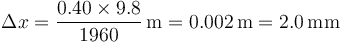
$\Delta x=\frac{0.40\times 9.8}{1960}\,\mathrm{m}=0.002\,\mathrm{m}=2.0\,\mathrm{mm}$

3 Velocidad de impacto

En la caída de la masa 1 se conserva la energía mecánica. En esta caída la energía potencial se transforma en cinética, cumpliéndose

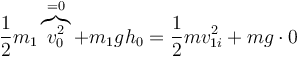
$\frac{1}{2}m_1\overbrace{v_0^2}^{=0}+m_1gh_0=\frac{1}{2}mv_{1i}^2+mg\cdot 0$

de donde

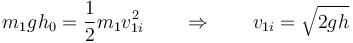
$m_1gh_0=\frac{1}{2}m_1v_{1i}^2\qquad\Rightarrow\qquad v_{1i}=\sqrt{2gh}$

siendo su valor numérico

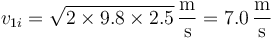
$v_{1i}=\sqrt{2\times 9.8\times 2.5}\,\frac{\mathrm{m}}{\mathrm{s}}=7.0\,\frac{\mathrm{m}}{\mathrm{s}}$

4 Nueva altura máxima

Cuando la masa 1 impacta con la 2 tenemos una colisión elástica en la que se conserva la cantidad de movimiento

$m_1v_{1i}+m_2\cdot 0 = m_1v_{1f}+m_2v_{2f}\,$

y por ser elástica el coeficiente de restitución es la unidad

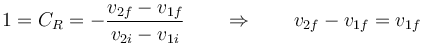
$1=C_R = -\frac{v_{2f}-v_{1f}}{v_{2i}-v_{1i}}\qquad\Rightarrow\qquad v_{2f}-v_{1f}=v_{1f}$

Esto es un sistema de dos ecuaciones con dos incógnitas, cuya solución para la velocidad de la masa 1 justo tras el choque es

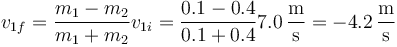
$v_{1f}=\frac{m_1-m_2}{m_1+m_2}v_{1i}=\frac{0.1-0.4}{0.1+0.4}7.0\,\frac{\mathrm{m}}{\mathrm{s}}=-4.2\,\frac{\mathrm{m}}{\mathrm{s}}$

La velocidad es negativa porque la masa rebota hacia arriba. La nueva altura máxima la hallamos aplicando de nuevo la ley de conservación de la energía mecánica

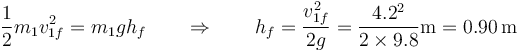
$\frac{1}{2}m_1v_{1f}^2 = m_1g h_f\qquad\Rightarrow\qquad h_f = \frac{v_{1f}^2}{2g}=\frac{4.2^2}{2\times 9.8}\mathrm{m}=0.90\,\mathrm{m}$

5 Máxima compresión

Tras la colisión, la plataforma adquiere también una cierta velocidad. Ésta se obtiene del sistema de ecuaciones del apartado anterior y el resultado es

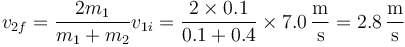
$v_{2f}=\frac{2m_1}{m_1+m_2}v_{1i}=\frac{2\times 0.1}{0.1+0.4}\times 7.0\,\frac{\mathrm{m}}{\mathrm{s}}=2.8\,\frac{\mathrm{m}}{\mathrm{s}}$

Esta velocidad inicial comprime el muelle. La máxima compresión se alcanza cuando toda la energía cinética se almacena como energía potencial elástica

$\frac{1}{2}m_2v_{2f}^2 + \frac{1}{2}k\cdot 0^2 = \frac{1}{2}m_2\cdot 0^2 + \frac{1}{2}kA^2$

es decir

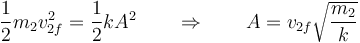
$\frac{1}{2}m_2v_{2f}^2=\frac{1}{2}kA^2 \qquad \Rightarrow\qquad A = v_{2f}\sqrt{\frac{m_2}{k}}$

siendo su valor

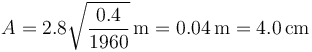
$A = 2.8\sqrt{\frac{0.4}{1960}}\,\mathrm{m}=0.04\,\mathrm{m}=4.0\,\mathrm{cm}$

6 Energía disipada

En el caso de la colisión completamente inelástica, el coeficiente de restitución es nulo. Esto implica que la masa 1 se funde con la 2. De la conservación de la cantidad de movimiento

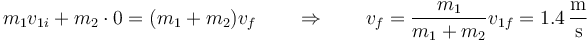
$m_1v_{1i}+m_2\cdot 0 = (m_1+m_2)v_f\qquad\Rightarrow\qquad v_f = \frac{m_1}{m_1+m_2}v_{1f}=1.4\,\frac{\mathrm{m}}{\mathrm{s}}$

La energía que se disipa en esta colisión es

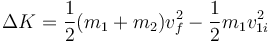
$\Delta K = \frac{1}{2}(m_1+m_2)v_f^2 - \frac{1}{2}m_1v_{1i}^2$

lo que da

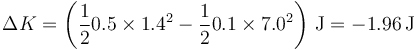
$\Delta K = \left(\frac{1}{2}0.5\times 1.4^2-\frac{1}{2}0.1\times 7.0^2\right)\,\mathrm{J} = -1.96\,\mathrm{J}$

7 Máxima compresión en el caso inelástico

Tras la colisión inelástica, el muelle se comprime adicionalmente por dos motivos:

Porque ahora la plataforma tiene más masa (ya que incluye a la otra masa)
Porque tiene una velocidad inicial

La compresión debida a la velocidad inicial la hallamos aplicando de nuevo la conservación de la energía mecánica, por lo que, operando igual que antes,

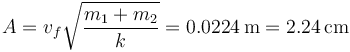
$A = v_f\sqrt{\frac{m_1+m_2}{k}} = 0.0224\,\mathrm{m}=2.24\,\mathrm{cm}$

La nueva compresión debida al peso cumple

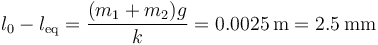
$l_0-l_\mathrm{eq}=\frac{(m_1+m_2)g}{k}=0.0025\,\mathrm{m}=2.5\,\mathrm{mm}$

Esto quiere decir que la nueva posición de equilibrio está medio milímetro por debajo de la anterior.

Sumando las dos deformaciones obtenemos una compresión total de 2.49 cm.

En realidad, hilando más fino, el cálculo correcto debe tener en cuenta que, puesto que la posición de equilibrio ha cambiado, inmediatamente tras la colisión las dos masas tienen una pequeña elongación inicial $x 0$ , de solo 0.5 mm. Por ello, siendo puntillosos, la aplicación de la ley de conservación de la energía da

$\frac{1}{2}(m_1+m_2)v_f^2+\frac{1}{2}kx_0^2=\frac{1}{2}kA^2\qquad\rightarrow\qquad A = \sqrt{x_0^2+\frac{(m_1+m_2)v_f^2}{k}}$

pero al ser tan pequeña esa elongación inicial, el resultado solo se diferencia del anterior en el sexto decimal (0.022366 en vez de 0.022361), por lo que este efecto puede ser ignorado en el cálculo de la amplitud.

@@ Línea 90: / Línea 90: @@
 <center><math>m_1v_{1i}+m_2\cdot 0 = (m_1+m_2)v_f\qquad\Rightarrow\qquad v_f = \frac{m_1}{m_1+m_2}v_{1f}=1.4\,\frac{\mathrm{m}}{\mathrm{s}}</math></center>
+La energía que se disipa en esta colisión es
+<center><math>\Delta K = \frac{1}{2}(m_1+m_2)v_f^2 - \frac{1}{2}m_1v_{1i}^2 </math></center>
+lo que da
+<center><math>\Delta K = \left(\frac{1}{2}0.5\times 1.4^2-\frac{1}{2}0.1\times 7.0^2\right)\,\mathrm{J} = -1.96\,\mathrm{J}</math></center>
 ==Máxima compresión en el caso inelástico==
+Tras la colisión inelástica, el muelle se comprime adicionalmente por dos motivos:
+* Porque ahora la plataforma tiene más masa (ya que incluye a la otra masa)
+* Porque tiene una velocidad inicial
+La compresión debida a la velocidad inicial la hallamos aplicando de nuevo la conservación de la energía mecánica, por lo que, operando igual que antes,
+<center><math>A = v_f\sqrt{\frac{m_1+m_2}{k}} = 0.0224\,\mathrm{m}=2.24\,\mathrm{cm}</math></center>
+La nueva compresión debida al peso cumple
+<center><math>l_0-l_\mathrm{eq}=\frac{(m_1+m_2)g}{k}=0.0025\,\mathrm{m}=2.5\,\mathrm{mm}</math></center>
+Esto quiere decir que la nueva posición de equilibrio está medio milímetro por debajo de la anterior.
+Sumando las dos deformaciones obtenemos una compresión total de 2.49&thinsp;cm.
+En realidad, hilando más fino, el cálculo correcto debe tener en cuenta que, puesto que la posición de equilibrio ha cambiado, inmediatamente tras la colisión las dos masas tienen una pequeña elongación inicial <math>x_0</math>, de solo 0.5&thinsp;mm. Por ello, siendo puntillosos, la aplicación de la ley de conservación de la energía da
+<center><math>
+\frac{1}{2}(m_1+m_2)v_f^2+\frac{1}{2}kx_0^2=\frac{1}{2}kA^2\qquad\rightarrow\qquad A = \sqrt{x_0^2+\frac{(m_1+m_2)v_f^2}{k}}</math></center>
+pero al ser tan pequeña esa elongación inicial, el resultado solo se diferencia del anterior en el sexto decimal (0.022366 en vez de 0.022361), por lo que este efecto puede ser ignorado en el cálculo de la amplitud.
 [[Categoría:Problemas de energía y leyes de conservación (GIE)]]

Masa que cae sobre resorte

De Laplace

última version al 19:09 28 ene 2014

Contenido

1 Enunciado

2 Compresión del resorte

3 Velocidad de impacto

4 Nueva altura máxima

5 Máxima compresión

6 Energía disipada

7 Máxima compresión en el caso inelástico

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES