Preguntas de test de herramientas matemáticas (GIE)
De Laplace
(→Ortogonalidad de dos vectores) |
|||
| (13 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | |||
==Suma de vectores ligados== | ==Suma de vectores ligados== | ||
Dados los vectores ligados de la figura, | Dados los vectores ligados de la figura, | ||
| Línea 21: | Línea 20: | ||
! D | ! D | ||
|} | |} | ||
| + | |||
| + | ;Solución: | ||
| + | La respuesta correcta es la '''<span style="color:red;">C<span>'''. | ||
| + | |||
| + | Para que dos vectores ligados se puedan sumar, deben tener un punto de aplicación común. Como este no es el caso, estos vectores no se pueden sumar. | ||
==Ángulo entre dos vectores== | ==Ángulo entre dos vectores== | ||
¿Qué ángulo forman los vectores <math>\vec{A}=24\vec{\imath}-32\vec{k}</math> y <math>\vec{B}=16\vec{\jmath}+12\vec{k}</math>? | ¿Qué ángulo forman los vectores <math>\vec{A}=24\vec{\imath}-32\vec{k}</math> y <math>\vec{B}=16\vec{\jmath}+12\vec{k}</math>? | ||
| - | * '''A''' 0.00 rad | + | :* '''A''' 0.00 rad |
| - | * '''B''' 1.07 rad | + | :* '''B''' 1.07 rad |
| - | * '''C''' 1.57 rad | + | :* '''C''' 1.57 rad |
| - | * '''D''' 2.07 rad | + | :* '''D''' 2.07 rad |
| + | |||
| + | ;Solución: | ||
| + | La respuesta correcta es la '''<span style="color:red;">D<span>'''. | ||
| + | |||
| + | Obtenemos el ángulo a partir del producto escalar de los dos vectores | ||
| + | |||
| + | <center><math>\vec{A}\cdot\vec{B}=|\vec{A}||\vec{B}|\cos(\alpha)\qquad\Rightarrow\qquad \alpha = \arccos\left(\frac{\vec{A}\cdot\vec{B}}{|\vec{A}||\vec{B}|}\right)</math></center> | ||
| + | |||
| + | Tenemos que | ||
| + | |||
| + | <center><math>\vec{A}\cdot\vec{B}=24\cdot 0+0\cdot 16+(-32)\cdot 12=-384</math></center> | ||
| + | |||
| + | y que | ||
| + | |||
| + | <center><math>|\vec{A}| = \sqrt{\vec{A}\cdot\vec{A}}=\sqrt{24^2+0^2+(-32)^2} = 40\qquad |\vec{B}| = \sqrt{\vec{B}\cdot\vec{B}}=\sqrt{0^2+16^2+12^2} = 20</math></center> | ||
| + | |||
| + | lo que nos da | ||
| + | |||
| + | <center><math>\cos(\alpha)=\frac{-384}{40\cdot20}=-\frac{12}{25}=-0.48\qquad\Rightarrow\qquad \alpha = 2.07\,\mathrm{rad}=118.7^\circ</math></center> | ||
==Posible igualdad vectorial== | ==Posible igualdad vectorial== | ||
| Línea 35: | Línea 58: | ||
<center><math>\vec{A}\cdot\vec{B} = \vec{A}\times\vec{B}</math></center> | <center><math>\vec{A}\cdot\vec{B} = \vec{A}\times\vec{B}</math></center> | ||
| - | * '''A''' Cuando <math>\vec{A}</math> y <math>\vec{B}</math> son paralelos. | + | :* '''A''' Cuando <math>\vec{A}</math> y <math>\vec{B}</math> son paralelos. |
| - | * '''B''' Cuando <math>\vec{A}</math> y <math>\vec{B}</math> son ortogonales. | + | :* '''B''' Cuando <math>\vec{A}</math> y <math>\vec{B}</math> son ortogonales. |
| - | * '''C''' No se cumple nunca. | + | :* '''C''' No se cumple nunca. |
| - | * '''D''' Cuando <math>\vec{A}</math> y <math>\vec{B}</math> forman un ángulo de 45°. | + | :* '''D''' Cuando <math>\vec{A}</math> y <math>\vec{B}</math> forman un ángulo de 45°. |
| + | |||
| + | ;Solución: | ||
| + | La respuesta correcta es la '''<span style="color:red;">C<span>'''. | ||
| + | |||
| + | El producto vectorial de dos vectores es una magnitud vectorial. El producto escalar, como su nombre indica, es una magnitud escalar. De acuerdo con el principio de homogeneidad, un escalar nunca puede ser igual a un vector. Por tanto, la igualdad no se cumple nunca. | ||
| + | |||
| + | ==Relación entre vectores== | ||
| + | Si <math>\vec{A}</math> y <math>\vec{B}</math> son dos vectores unitarios, indique cuándo se cumple la igualdad | ||
| + | |||
| + | <center><math>\vec{A}\cdot\vec{B} = |\vec{A}\times\vec{B}|</math></center> | ||
| + | |||
| + | :* '''A''' Cuando <math>\vec{A}</math> y <math>\vec{B}</math> forman un ángulo de 45°. | ||
| + | :* '''B''' Cuando <math>\vec{A}</math> y <math>\vec{B}</math> son paralelos. | ||
| + | :* '''C''' Cuando <math>\vec{A}</math> y <math>\vec{B}</math> son ortogonales. | ||
| + | :* '''D''' No se cumple nunca. | ||
| + | |||
| + | ;Solución | ||
| + | La respuesta correcta es la '''<span style="color:red;">A<span>'''. | ||
| + | |||
| + | A diferencia de la anterior, ahora se comparan dos escalares, lo que sí es posible. la igualdad se da cuando | ||
| + | |||
| + | <center><math>\mathrm{sen}(\alpha)=\cos(\alpha)\qquad\Rightarrow\qquad \alpha=\frac{\pi}{4}=45^\circ</math></center> | ||
==Otra posible igualdad vectorial== | ==Otra posible igualdad vectorial== | ||
Sean <math>\vec{A}</math>, <math>\vec{B}</math> y <math>\vec{C}</math> vectores arbitrarios no nulos. ¿Cuál de las siguientes afirmaciones es cierta siempre? | Sean <math>\vec{A}</math>, <math>\vec{B}</math> y <math>\vec{C}</math> vectores arbitrarios no nulos. ¿Cuál de las siguientes afirmaciones es cierta siempre? | ||
| - | * '''A''' <math>\vec{A}\cdot\vec{B} = \vec{B}\cdot\vec{A}</math> | + | :* '''A''' <math>\vec{A}\cdot\vec{B} = \vec{B}\cdot\vec{A}</math> |
| - | * '''B''' <math>(\vec{A}\cdot\vec{B})\vec{C} = \vec{A}(\vec{B}\cdot\vec{C})</math> | + | :* '''B''' <math>(\vec{A}\cdot\vec{B})\vec{C} = \vec{A}(\vec{B}\cdot\vec{C})</math> |
| - | * '''C''' <math>\vec{A}\times\vec{B} = \vec{B}\times\vec{A}</math> | + | :* '''C''' <math>\vec{A}\times\vec{B} = \vec{B}\times\vec{A}</math> |
| - | * '''D''' <math>(\vec{A}\times\vec{B})\times\vec{C} = \vec{A}\times(\vec{B}\times\vec{C})</math> | + | :* '''D''' <math>(\vec{A}\times\vec{B})\times\vec{C} = \vec{A}\times(\vec{B}\times\vec{C})</math> |
| + | |||
| + | ;Solución: | ||
| + | La respuesta correcta es la '''<span style="color:red;">A<span>'''. | ||
| + | |||
| + | Es evidente que la respuesta A es correcta, ya que el producto escalar es conmutativo. Para ver por qué las otras son incorrectas, observemos que: | ||
| + | |||
| + | * En la respuesta B tenemos en el primer miembro un vector paralelo a <math>\vec{C}</math> y en el segundo uno paralelo a <math>\vec{A}</math>, por lo que no se da la igualdad. | ||
| + | * En la respuesta C tenemos la posible propiedad conmutativa del producto vectorial, pero esta no se cumple, ya que el producto vectorial es anticonmutativo | ||
| + | |||
| + | <center><math>\vec{A}\times\vec{B}=-\vec{B}\times\vec{A}</math></center> | ||
| + | |||
| + | * En la respuesta D tenemos dos casos de doble producto vectorial, cuyos desarrollos son: | ||
| + | |||
| + | <center><math>(\vec{A}\times\vec{B})\times\vec{C} = (\vec{C}\cdot\vec{A})\vec{B}-(\vec{C}\cdot\vec{B})\vec{A}\qquad\qquad | ||
| + | \vec{A}\times(\vec{B}\times\vec{C})=(\vec{A}\cdot\vec{C})\vec{B}-(\vec{A}\cdot\vec{B})\vec{C}</math></center> | ||
| + | |||
| + | : El primer término si es el mismo en los dos desarrollos, pero el segundo no, por lo que las expresiones son diferentes. | ||
==Área de un triángulo== | ==Área de un triángulo== | ||
Dados tres puntos del espacio A, B y C, siendo O el origen de coordenadas, ¿cómo podemos hallar el área del triángulo que definen? | Dados tres puntos del espacio A, B y C, siendo O el origen de coordenadas, ¿cómo podemos hallar el área del triángulo que definen? | ||
| - | * '''A''' <math>\overrightarrow{AB}\cdot\overrightarrow{AC}</math> | + | :* '''A''' <math>\overrightarrow{AB}\cdot\overrightarrow{AC}</math> |
| - | * '''B''' <math>(\overrightarrow{AB}\cdot\overrightarrow{AC})/2</math> | + | :* '''B''' <math>(\overrightarrow{AB}\cdot\overrightarrow{AC})/2</math> |
| - | * '''C''' <math>|\overrightarrow{AB}\times\overrightarrow{AC}|/2</math> | + | :* '''C''' <math>|\overrightarrow{AB}\times\overrightarrow{AC}|/2</math> |
| - | * '''D''' <math>\overrightarrow{OB}\cdot(\overrightarrow{OB}\times\overrightarrow{OC})</math> | + | :* '''D''' <math>\overrightarrow{OB}\cdot(\overrightarrow{OB}\times\overrightarrow{OC})</math> |
| + | |||
| + | ;Solución: | ||
| + | La respuesta correcta es la '''<span style="color:red;">C<span>'''. | ||
| + | |||
| + | El área de un triángulo es una magnitud escalar, lo que ya descarta la respuesta B. Obtenemos el área de un triángulo como la mitad del área del paralelogramo definido por dos de sus lados. A su vez, el área de un paralelogramo es el módulo del producto vectorial de estos dos vectores. | ||
| + | |||
| + | Si los vértices son A, B y C, dos vectores que dan los lados son <math>\overrightarrow{AB}</math> y <math>\overrightarrow{AC}</math>, por lo que el área buscada es | ||
| + | |||
| + | <center><math>S = \frac{1}{2}\left|\overrightarrow{AB}\times\overrightarrow{AC}\right|</math></center> | ||
| + | |||
| + | ==Comprobación de identidades== | ||
| + | ¿Cuál de las siguientes afirmaciones no es necesariamente incorrecta? Los símbolos son los usuales en cinemática | ||
| + | |||
| + | :* '''A''' <math>\vec{r}=(\vec{v}-\vec{a}t)/|\vec{a}-\vec{v}t|</math> | ||
| + | :* '''B''' <math>\Delta t=(\Delta \vec{r})/\vec{v}</math> | ||
| + | :* '''C''' <math>R=|\vec{v}|^3/|\vec{v}\times\vec{a}|</math> | ||
| + | :* '''D''' <math>\vec{r}\cdot(\vec{a}\cdot\vec{v})= (\vec{v}\cdot\vec{v})\cdot\vec{v}</math> | ||
| + | ;Solución: | ||
| + | La respuesta correcta es la '''<span style="color:red;">C<span>'''. | ||
| + | |||
| + | n la respuesta A no se cumple la homogeneidad dimensional, ya que el producto de una velocidad por un tiempo tiene las dimensiones de una posición, no de una aceleración. | ||
| + | |||
| + | En la respuesta B se divide por un vector. | ||
| + | |||
| + | En la D aparece una operación inexistente, el doble producto escalar. | ||
| + | |||
| + | ==Ángulo entre dos diagonales== | ||
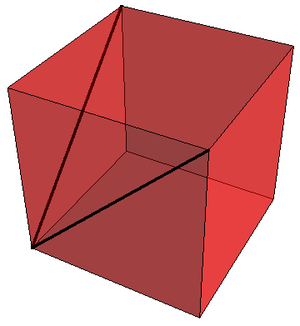
| + | Se tienen dos vectores a lo largo de las diagonales de las caras de un cubo, con el mismo punto de aplicación. ¿Qué ángulo forman? | ||
| + | |||
| + | <center>[[Archivo:diagonales-cubo.png|300px]]</center> | ||
| + | |||
| + | :* '''A''' π/4 | ||
| + | :* '''B''' π/6 | ||
| + | :* '''C''' π/2 | ||
| + | :* '''D''' π/3 | ||
| + | ;Solución: | ||
| + | La respuesta correcta es la '''<span style="color:red;">D<span>'''. | ||
| + | |||
| + | Es fácil ver que el ángulo es de π/3 simplemente completando un triángulo equilátero añadiendo una tercera diagonal: | ||
| + | |||
| + | <center>[[Archivo:diagonales-cubo-02.png|300px]]</center> | ||
| + | |||
| + | Puesto que los tres ángulos de un triángulo equilátero son de 60°, se llega a la respuesta correcta. | ||
| + | |||
| + | No obstante, también puede probarse analíticamente de forma sencilla. Los vectores que definen las diagonales son | ||
| + | |||
| + | <center><math>\vec{v}_1=\vec{\imath}+\vec{k}\qquad\qquad \vec{v}_2=\vec{\jmath}+\vec{k}</math></center> | ||
| + | |||
| + | y el coseno del ángulo que forman vale | ||
| + | |||
| + | <center><math>\cos(\alpha)=\frac{\vec{v}_1\cdot\vec{v}_2}{|\vec{v}_1||\vec{v}_2|}=\frac{0+0+1}{\sqrt{2}\sqrt{2}}=\frac{1}{2}</math></center> | ||
| + | |||
| + | y por tanto | ||
| + | |||
| + | <center><math>\alpha=\arccos\left(\frac{1}{2}\right)=\frac{\pi}{3}</math></center> | ||
| + | de un cubo, con el mismo punto de aplicación. ¿Qué ángulo forman? | ||
| + | |||
| + | ==Ecuaciones con vectores== | ||
| + | Dados dos vectores arbitrarios <math>\vec{a}</math> y <math>\vec{b}</math>, ¿cuál de las siguientes afirmaciones es cierta, en general? | ||
| + | |||
| + | :*'''A''' <math>|\vec{a}||\vec{b}| = |\vec{a}\cdot\vec{b}|+|\vec{a}\times\vec{b}|</math> | ||
| + | :*'''B''' <math>(\vec{a}\times\vec{b})\times\vec{a}=\vec{0}</math> | ||
| + | :*'''C''' <math>(\vec{a}\times\vec{b})\cdot\vec{a}=0</math> | ||
| + | :*'''D''' <math>(\vec{a}\cdot\vec{b})\vec{a}=|\vec{a}|^2\vec{b}</math> | ||
| + | |||
| + | ;Solución: | ||
| + | La respuesta correcta es la '''<span style="color:red">C</span>'''. | ||
| + | |||
| + | ==Ortogonalidad de dos vectores== | ||
| + | Dados dos vectores no nulos, <math>\vec{a}</math> y <math>\vec{b}</math>, ¿cuándo son perpendiculares su suma <math>\vec{a}+\vec{b}</math> y su diferencia <math>\vec{a}-\vec{b}</math>? | ||
| + | |||
| + | :* '''A''' Cuando <math>a</math> y <math>b</math> tienen el mismo módulo. | ||
| + | :* '''B''' Nunca. | ||
| + | :* '''C''' Cuando <math>a</math> y <math>b</math> son paralelos. | ||
| + | :* '''D''' Cuando <math>a</math> y <math>b</math> son ortogonales. | ||
| + | |||
| + | ;Solución | ||
| + | La respuesta correcta es la '''<span style="color:red;">A<span>'''. | ||
| + | |||
| + | Dos vectores son ortogonales cuando se anula su producto escalar | ||
| + | |||
| + | <center><math>0 = (\vec{a}+\vec{b})\cdot(\vec{a}-\vec{b})=\vec{a}\cdot\vec{a}-\vec{b}\cdot\vec{b}=|\vec{a}|^2-|\vec{b}|^2</math></center> | ||
| + | |||
| + | y esta cantidad se anula cuando son iguales los módulos. | ||
| + | |||
| + | ==Ecuación vectorial== | ||
| + | Sea <math>O</math> un punto fijo del espacio, <math>\vec{A}</math> y <math>\vec{C}</math> dos vectores constantes no nulos y <math>P</math> un punto del espacio que verifica <math>\vec{C}\times\overrightarrow{OP}=\vec{A}</math>. El conjunto de todos los puntos <math>P</math> forma… | ||
| + | :* '''A''' una recta paralela a <math>\vec{C}</math> y que no pasa por O. | ||
| + | :* '''B''' un plano perpendicular a <math>\vec{C}</math>. | ||
| + | :* '''C''' una recta paralela a <math>\vec{C}</math> y que pasa por O. | ||
| + | :* '''D''' un plano perpendicular a <math>\vec{A}</math>. | ||
| + | ;Solución: | ||
| + | La respuesta correcta es la '''<span style="color:red;">A<span>'''. | ||
[[Categoría:Problemas de herramientas matemáticas (GIE)]] | [[Categoría:Problemas de herramientas matemáticas (GIE)]] | ||
[[Categoría:Preguntas de test de Física I (GIE)]] | [[Categoría:Preguntas de test de Física I (GIE)]] | ||
última version al 18:04 21 oct 2017
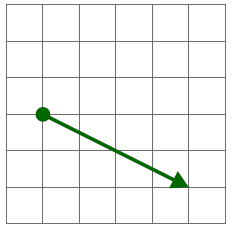
1 Suma de vectores ligados
Dados los vectores ligados de la figura,
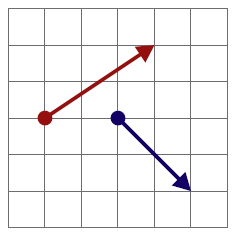
¿cuánto vale su suma vectorial?
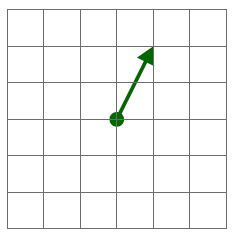
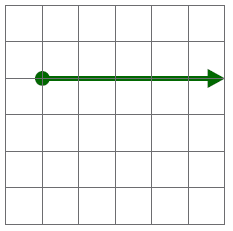
| 
|
| A | B |
|---|---|
| 
|
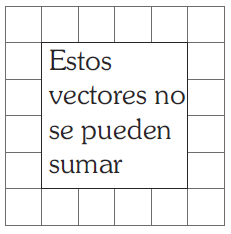
| C | D |
- Solución
La respuesta correcta es la C.
Para que dos vectores ligados se puedan sumar, deben tener un punto de aplicación común. Como este no es el caso, estos vectores no se pueden sumar.
2 Ángulo entre dos vectores
¿Qué ángulo forman los vectores 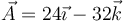 y
y 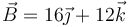 ?
?
- A 0.00 rad
- B 1.07 rad
- C 1.57 rad
- D 2.07 rad
- Solución
La respuesta correcta es la D.
Obtenemos el ángulo a partir del producto escalar de los dos vectores
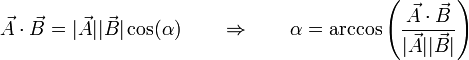
Tenemos que
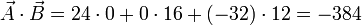
y que
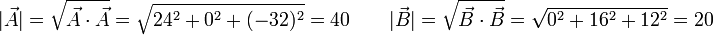
lo que nos da
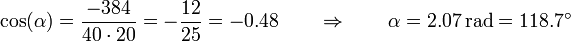
3 Posible igualdad vectorial
Si  y
y  son dos vectores unitarios, indique cuándo se cumple la igualdad
son dos vectores unitarios, indique cuándo se cumple la igualdad
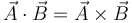
- A Cuando
 y
y  son paralelos.
son paralelos.
- B Cuando
 y
y  son ortogonales.
son ortogonales.
- C No se cumple nunca.
- D Cuando
 y
y  forman un ángulo de 45°.
forman un ángulo de 45°.
- A Cuando
- Solución
La respuesta correcta es la C.
El producto vectorial de dos vectores es una magnitud vectorial. El producto escalar, como su nombre indica, es una magnitud escalar. De acuerdo con el principio de homogeneidad, un escalar nunca puede ser igual a un vector. Por tanto, la igualdad no se cumple nunca.
4 Relación entre vectores
Si  y
y  son dos vectores unitarios, indique cuándo se cumple la igualdad
son dos vectores unitarios, indique cuándo se cumple la igualdad
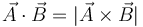
- A Cuando
 y
y  forman un ángulo de 45°.
forman un ángulo de 45°.
- B Cuando
 y
y  son paralelos.
son paralelos.
- C Cuando
 y
y  son ortogonales.
son ortogonales.
- D No se cumple nunca.
- A Cuando
- Solución
La respuesta correcta es la A.
A diferencia de la anterior, ahora se comparan dos escalares, lo que sí es posible. la igualdad se da cuando
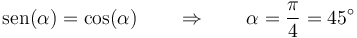
5 Otra posible igualdad vectorial
Sean  ,
,  y
y  vectores arbitrarios no nulos. ¿Cuál de las siguientes afirmaciones es cierta siempre?
vectores arbitrarios no nulos. ¿Cuál de las siguientes afirmaciones es cierta siempre?
- A
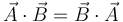
- B
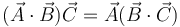
- C
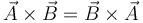
- D
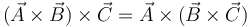
- A
- Solución
La respuesta correcta es la A.
Es evidente que la respuesta A es correcta, ya que el producto escalar es conmutativo. Para ver por qué las otras son incorrectas, observemos que:
- En la respuesta B tenemos en el primer miembro un vector paralelo a
 y en el segundo uno paralelo a
y en el segundo uno paralelo a  , por lo que no se da la igualdad.
, por lo que no se da la igualdad.
- En la respuesta C tenemos la posible propiedad conmutativa del producto vectorial, pero esta no se cumple, ya que el producto vectorial es anticonmutativo
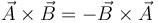
- En la respuesta D tenemos dos casos de doble producto vectorial, cuyos desarrollos son:

- El primer término si es el mismo en los dos desarrollos, pero el segundo no, por lo que las expresiones son diferentes.
6 Área de un triángulo
Dados tres puntos del espacio A, B y C, siendo O el origen de coordenadas, ¿cómo podemos hallar el área del triángulo que definen?
- A
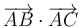
- B
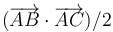
- C
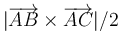
- D
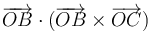
- A
- Solución
La respuesta correcta es la C.
El área de un triángulo es una magnitud escalar, lo que ya descarta la respuesta B. Obtenemos el área de un triángulo como la mitad del área del paralelogramo definido por dos de sus lados. A su vez, el área de un paralelogramo es el módulo del producto vectorial de estos dos vectores.
Si los vértices son A, B y C, dos vectores que dan los lados son 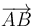 y
y 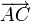 , por lo que el área buscada es
, por lo que el área buscada es
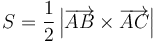
7 Comprobación de identidades
¿Cuál de las siguientes afirmaciones no es necesariamente incorrecta? Los símbolos son los usuales en cinemática
- A
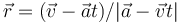
- B
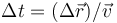
- C
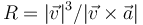
- D
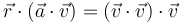
- A
- Solución
La respuesta correcta es la C.
n la respuesta A no se cumple la homogeneidad dimensional, ya que el producto de una velocidad por un tiempo tiene las dimensiones de una posición, no de una aceleración.
En la respuesta B se divide por un vector.
En la D aparece una operación inexistente, el doble producto escalar.
8 Ángulo entre dos diagonales
Se tienen dos vectores a lo largo de las diagonales de las caras de un cubo, con el mismo punto de aplicación. ¿Qué ángulo forman?
- A π/4
- B π/6
- C π/2
- D π/3
- Solución
La respuesta correcta es la D.
Es fácil ver que el ángulo es de π/3 simplemente completando un triángulo equilátero añadiendo una tercera diagonal:

Puesto que los tres ángulos de un triángulo equilátero son de 60°, se llega a la respuesta correcta.
No obstante, también puede probarse analíticamente de forma sencilla. Los vectores que definen las diagonales son

y el coseno del ángulo que forman vale
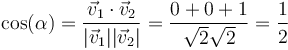
y por tanto
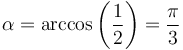
de un cubo, con el mismo punto de aplicación. ¿Qué ángulo forman?
9 Ecuaciones con vectores
Dados dos vectores arbitrarios  y
y  , ¿cuál de las siguientes afirmaciones es cierta, en general?
, ¿cuál de las siguientes afirmaciones es cierta, en general?
- A
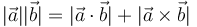
- B
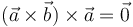
- C
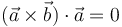
- D
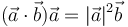
- A
- Solución
La respuesta correcta es la C.
10 Ortogonalidad de dos vectores
Dados dos vectores no nulos,  y
y  , ¿cuándo son perpendiculares su suma
, ¿cuándo son perpendiculares su suma 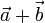 y su diferencia
y su diferencia 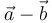 ?
?
- A Cuando a y b tienen el mismo módulo.
- B Nunca.
- C Cuando a y b son paralelos.
- D Cuando a y b son ortogonales.
- Solución
La respuesta correcta es la A.
Dos vectores son ortogonales cuando se anula su producto escalar
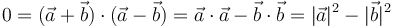
y esta cantidad se anula cuando son iguales los módulos.
11 Ecuación vectorial
Sea O un punto fijo del espacio,  y
y  dos vectores constantes no nulos y P un punto del espacio que verifica
dos vectores constantes no nulos y P un punto del espacio que verifica 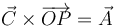 . El conjunto de todos los puntos P forma…
. El conjunto de todos los puntos P forma…
- A una recta paralela a
 y que no pasa por O.
y que no pasa por O.
- B un plano perpendicular a
 .
.
- C una recta paralela a
 y que pasa por O.
y que pasa por O.
- D un plano perpendicular a
 .
.
- A una recta paralela a
- Solución
La respuesta correcta es la A.





