Coeficientes de inducción mutua y autoinducción (GIE)
De Laplace
(→Caso de dos espiras) |
m (→Caso de dos espiras) |
||
| (29 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | == | + | ==Autoinducción== |
| - | + | ===Concepto=== | |
| - | + | Cuando se tiene una espira cerrada por la cual circula una corriente variable en el tiempo, esa corriente produce un campo magnético (de acuerdo con la ley de Biot y Savart), el cual será también variable en el tiempo. Este campo tendrá un flujo magnético a través de la propia espira, y será también variable en el tiempo. De acuerdo con la ley de Faraday, un flujo magnético variable en el tiempo induce una fuerza electromotriz en la espira. Esta f.e.m. hay que añadirla a las otras que hubiera y por tanto modifica a la propia corriente. | |
| - | + | <center>[[Archivo:Ejemplo-autoinduccion.png]]</center> | |
| - | + | ||
| - | Dada una curva cerrada <math> | + | Por tanto, una corriente variable en el tiempo produce un efecto sobre sí misma, debido al campo magnético que genera. Este efecto se denomina autoinducción. |
| + | |||
| + | ===Coeficiente de autoinducción=== | ||
| + | El campo magnético debido a una corriente eléctrica, según la ley de Biot y Savart es proporcional a la intensidad de corriente que lo causa. Asimismo, este campo verifica la regla de la mano derecha respecto a la corriente. | ||
| + | |||
| + | Dada una curva cerrada <math>C</math>, el flujo magnético lo da la integral | ||
<center><math>\Phi_m = \int_S \vec{B}\cdot \mathrm{d}\vec{S}</math></center> | <center><math>\Phi_m = \int_S \vec{B}\cdot \mathrm{d}\vec{S}</math></center> | ||
| - | siendo S una superficie abierta apoyada en | + | siendo S una superficie abierta apoyada en C y orientada según la regla de la mano derecha (es decir, en el mismo sentido que el campo magnético). |
| - | <center>[[Archivo: | + | <center>[[Archivo:Autoflujo-magnetico.png]]</center> |
| - | + | Al ser el campo proporcional a la intensidad de corriente, también lo será su flujo | |
| - | + | ||
<center><math>\Phi_m = L I\,</math></center> | <center><math>\Phi_m = L I\,</math></center> | ||
| Línea 21: | Línea 24: | ||
siendo <math>L</math> el denominado ''coeficiente de autoinducción'', cuya unidad es el Henrio (H) | siendo <math>L</math> el denominado ''coeficiente de autoinducción'', cuya unidad es el Henrio (H) | ||
| - | <center><math>1\,\mathrm{H} = \frac{1\,\mathrm{T}\cdot \mathrm{m}^2}{\mathrm{A}} = | + | <center><math>1\,\mathrm{H} = \frac{1\,\mathrm{T}\cdot \mathrm{m}^2}{\mathrm{A}} = 1\,\Omega\cdot \mathrm{s} |
| - | 1\,\Omega\cdot \mathrm{s} | + | |
</math></center> | </math></center> | ||
| - | ===Inducción mutua==== | + | Por aplicación de la regla de la mano derecha, se llega a que este coeficiente es siempre positivo. |
| + | |||
| + | El coeficiente de autoinducción es una propiedad global del circuito. Sin embargo, dado a que a menudo el campo magnético es mucho más intenso en las bobinas presentes, puede considerarse que el flujo magnético se concentra en ellas y asignarle el valor de la autoinducción como algo localizado. | ||
| + | |||
| + | La fuerza electromotriz debida a la presencia de la autoinducción se calcula mediante la derivada | ||
| + | |||
| + | <center><math>\mathcal{E}=-\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}=-\frac{\mathrm{d}\ }{\mathrm{d}t}(LI)</math></center> | ||
| + | |||
| + | Si la espira es rígida (lo que es lo habitual), el coeficiente de autoinducción es constante y puede salir de la derivada, quedando el resultado más familiar | ||
| + | |||
| + | <center><math>\mathcal{E}=-L\frac{\mathrm{d}I}{\mathrm{d}t}</math></center> | ||
| + | |||
| + | ===Comportamiento de un circuito=== | ||
| + | Supongamos una espira rígida caracterizada por una resistencia eléctrica <math>R</math> y un coeficiente de autoinducción <math>L</math>. Si esta espira se encuentra sometida a una fuera electromotriz externa (causada por un campo magnético aplicado, o por un generador), la ecuación para la corriente que pasa por el circuito es | ||
| + | |||
| + | <center><math>IR=\mathcal{E}_g+\mathcal{E}_L = \mathcal{E}_g-L\frac{\mathrm{d}I}{\mathrm{d}t}\qquad\Rightarrow\qquad L\frac{\mathrm{d}I}{\mathrm{d}t}+IR = \mathcal{E}_g</math></center> | ||
| + | |||
| + | Podemos leer esta ecuación diferencial como que existe solo una fuente de tensión, <math>\mathcal{E}_g</math> que alimenta a dos elementos en serie: | ||
| + | |||
| + | <center><math>\mathcal{E}_g = (\Delta V)_L+(\Delta V)_R</math></center> | ||
| + | |||
| + | * Una resistencia R sin autoinducción, <math>(\Delta V)_R = IR</math> | ||
| + | * Una autoinducción L sin resistencia, <math>(\Delta V)_L = L(\mathrm{d}I/\mathrm{d}t)</math>´. que se representa con un nuevo símbolo | ||
| + | |||
| + | Así, lo que podría ser una simple anilla conductora sometida a un campo externo se modela por tres elementos de circuito. Nunca hay que olvidar que esto es un modelo. No tenemos una resistencia por un lado y una autoinducción por otro. Las dos propiedades van juntas en el mismo elemento real. | ||
| + | |||
| + | Este voltaje <math>\Delta V_L</math> es justamente el que mediría un voltímetro conectado a los extremos de una bobina ideal. Para ver por qué el signo es positivo y no negativo hay que clarificar el convenio de signos. | ||
| + | |||
| + | Supongamos un elemento de circuito, como puede ser un resistor, que tiene dos extremos A y B. Suponemos que la corriente es positiva si va de A a B (y negativa en caso contrario) Si ahora situamos un voltímetro puesto en paralelo entre los dos extremos tomamos la polaridad de forma que el voltímetro mide el voltaje | ||
| + | |||
| + | <center><math>\Delta V = V_A-V_B\,</math></center> | ||
| + | |||
| + | (si es necesario se indica con signos + en en lado de A y - en el de B). En este caso, para un resistor se cumple laey de Ohm | ||
| + | |||
| + | <center><math>\Delta V_R = V_A - V_B = IR</math></center> | ||
| + | |||
| + | Obsérvese que si se cambia el criterio de signos para la corriente o para el voltaje, esta ley aparecería con signo cambiado. | ||
| + | |||
| + | Una expresión análoga se tiene para el caso de un condensador | ||
| + | |||
| + | <center><math>\Delta V_C = \frac{Q}{C}</math></center> | ||
| + | |||
| + | donde, para que el criterio de signos sea el correcto, Q representa la carga de la placa conectada a A. | ||
| + | |||
| + | Si ahora lo aplicamos a un generador observamos que, dado que la corriente en un generador entra por su polo negativo y sale por el positivo, se cumple | ||
| + | |||
| + | <center><math>\Delta V = V_A-V_B = V_N-V_P = -(V_P-V_N)=-(\mathcal{E}-Ir)=Ir-\mathcal{E}</math></center> | ||
| + | |||
| + | que podemos leer como una asociación en serie de una resistencia interna y una fuente ideal. | ||
| + | |||
| + | Si este caso lo particularizamos para una autoinducción | ||
| + | |||
| + | <center><math>\mathcal{E}_L=-L\frac{\mathrm{d}I}{\mathrm{d}t}\qquad\Rightarrow\qquad \Delta V= Ir+L\frac{\mathrm{d}I}{\mathrm{d}t} = \Delta V_R+\Delta V_L</math></center> | ||
| + | |||
| + | ===Corrientes de cierre y de ruptura=== | ||
| + | |||
| + | La presencia de la autoinducción afecta a la corriente que circula por el circuito. | ||
| + | |||
| + | Consideremos el caso particular de una señal escalón, es decir, que la fuente externa se conecta en t=0 cerrando el circuito y partir de ese momento tiene un valor <math>\mathcal{E}_0</math>. Si no hubiera autoinducción, el efecto sería la aparición de una corriente continua de valor | ||
| + | |||
| + | <center><math>I_\mathrm{dc}=\frac{\mathcal{E}_0}{R}</math></center> | ||
| + | |||
| + | Debido a la autoinducción la conducta es un poco más complicada. Tenemos la ecuación | ||
| + | |||
| + | <center><math>L\frac{\mathrm{d}I}{\mathrm{d}t}+IR = \mathcal{E}_0\qquad\qquad I(0) = 0</math></center> | ||
| + | |||
| + | La segunda condición viene de que justo al cerrar el interruptor aun no circula corriente por la espira. La solución de esta ecuación diferencial es | ||
| + | |||
| + | <center><math>I(t) = \frac{\mathcal{E}_0}{R}\left(1-\mathrm{e}^{-t/\tau}\right)\qquad\qquad \tau = \frac{L}{R}</math></center> | ||
| + | |||
| + | Esta solución nos dice que la corriente no se establece instantáneamente, sino que tiende exponencialmente a su valor estacionario. El tiempo que tarda es proporcional a <math>\tau = L/R</math>, de forma que cuando ha pasado 4 o 5 veces el valor de tau ya se puede decir que la corriente ha llegado a su valor estacionario. El efecto de la autoinducción es entonces el de retardar este establecimiento. Como consecuencia de la ley de Lenz, la f.e.m. inducida se opone al cambio y retrasa su variación, tanto más cuanto mayor sea el coeficiente de autoinducción L. | ||
| + | |||
| + | Supongamos ahora el mismo circuito, con la misma fuente, en el que ha pasado el tiempo suficiente para que circule una corriente continua <math>I_0</math>, si ahora cortocircuitamos el generador (es decir, lo mantenemos cerrado pero sin fuente externa que lo alimente), ¿desaparece instantáneamente la corriente? No. La ecuación diferencial para la corriente es ahora | ||
| + | |||
| + | <center><math>L\frac{\mathrm{d}I}{\mathrm{d}t}+IR = 0\qquad\qquad I(0) = I_0</math></center> | ||
| + | |||
| + | y su solución | ||
| + | |||
| + | <center><math>I(t) = I_0\mathrm{e}^{-t/\tau}\qquad\qquad \tau = \frac{L}{R}</math></center> | ||
| + | |||
| + | que quiere decir que la corriente tarda un tiempo del orden de tau en extinguirse. De nuevo, el efecto de la autoinducción es retrasar el cambio, manteniendo una corriente aunque ya no haya fuente externa que la produzca. Este efecto es transitorio y usualmente muy breve. Esta es la causa de que al desconectar un aparato salte una chispa. la autoinducción intenta mantener una corriente circulando por el circuito. | ||
| + | |||
| + | ===Caso de una bobina=== | ||
| + | El ejemplo más sencillo de autoinducción lo da una bobina cilíndrica de radio <math>a</math>, gran longitud <math>h</math> y número de espiras <math>N</math>. Cuando por ella pasa una intensidad de corriente <math>I</math>, el campo magnético que produce en su interior es aproximadamente | ||
| + | |||
| + | <center><math>\vec{B}\simeq \frac{\mu_0NI}{h}\vec{k}</math></center> | ||
| + | |||
| + | siendo <math>\vec{k}</math> el unitario a lo largo del eje. El campo es nulo en su exterior. Para hallar el flujo de este campo a través de la propia bobina hay que tener en cuenta que el campo no atraviesa una sola espira, sino todas ellas, por lo que | ||
| + | |||
| + | <center><math>\Phi_m = N\phi\,</math></center> | ||
| + | |||
| + | siendo <math>\phi\,</math> el flujo a través de una espira | ||
| + | |||
| + | <center><math>\phi = \left(\frac{\mu_0NI}{h}\right)\pi a^2</math></center> | ||
| + | |||
| + | lo que nos da el coeficiente de autoinducción | ||
| + | |||
| + | <center><math>L = \frac{\mu_0N^2S}{h}\qquad \qquad S = \pi a^2</math></center> | ||
| + | |||
| + | Esta bobina también tiene una resistencia eléctrica, por tratarse de un hilo de cobre enrollado. Su valor es | ||
| + | |||
| + | <center><math>R = \frac{l}{\sigma A}=\frac{2\pi Na}{\sigma A}</math></center> | ||
| + | |||
| + | siendo A la sección transversal de cable (no de la bobina; esa es S). | ||
| + | |||
| + | ===Lectura de un voltímetro=== | ||
| + | Un voltímetro es un dispositivo que mide el voltaje (es decir, la integral del campo eléctrico), a lo largo del propio voltímetro. Si este aparato se halla en una región donde no hay campo magnético, esta medida coincide con la diferencia de potencial eléctrico. | ||
| + | |||
| + | Si tenemos una bobina, en la cual la corriente entra por su extremo A y sale por su extremo B, y colocamos un voltímetro entre sus extremos, la lectura que marca es | ||
| + | |||
| + | <center><math>\Delta V = V_A-V_B = -(V_B-V_A) = -(\mathcal{E}-IR)=+L\frac{\mathrm{d}I}{\mathrm{d}t}+IR</math></center> | ||
| + | |||
| + | que de nuevo leemos como que tenemos dos elementos puestos en serie, aunque tengamos un solo elemento real. | ||
| + | |||
| + | ==Inducción mutua== | ||
| + | ===Concepto=== | ||
Si en lugar de una sola espira tenemos un conjunto de ellas, por las cuales circulan corrientes <math>I_k</math>, el flujo a través de una superficie <math>S_i</math> apoyada en la espira <math>i</math> tendrá una contribución por cada una de las espiras | Si en lugar de una sola espira tenemos un conjunto de ellas, por las cuales circulan corrientes <math>I_k</math>, el flujo a través de una superficie <math>S_i</math> apoyada en la espira <math>i</math> tendrá una contribución por cada una de las espiras | ||
| Línea 45: | Línea 162: | ||
Para conocer el signo de cada coeficiente debe aplicarse el criterio siguiente: | Para conocer el signo de cada coeficiente debe aplicarse el criterio siguiente: | ||
| - | * Para cada espira <math> | + | * Para cada espira <math>C_i</math> se asigna un sentido de recorrido de la corriente. |
| - | * La regla de la mano derecha establece el sentido de la normal <math>\vec{n}_i</math> a la superficie <math>S_i</math> apoyada en <math> | + | * La regla de la mano derecha establece el sentido de la normal <math>\vec{n}_i</math> a la superficie <math>S_i</math> apoyada en <math>C_i</math>. |
| - | * El campo magnético producido por la espira <math> | + | * El campo magnético producido por la espira <math>C_k</math> verifica asimismo la regla de la mano derecha respecto de la corriente que lo produce. |
* El flujo del campo magnético es positivo si <math>\vec{B}</math> y <math>\vec{n}</math> van el mismo sentido y negativo en caso contrario. | * El flujo del campo magnético es positivo si <math>\vec{B}</math> y <math>\vec{n}</math> van el mismo sentido y negativo en caso contrario. | ||
* Por tanto, si el campo <math>\vec{B}_k</math> entra en la espira <math>i</math> según la orientación dada por la regla de la mano derecha para esta espira, <math>L_{ik}>0</math>. En caso contrario <math>L_{ik}<0</math>. | * Por tanto, si el campo <math>\vec{B}_k</math> entra en la espira <math>i</math> según la orientación dada por la regla de la mano derecha para esta espira, <math>L_{ik}>0</math>. En caso contrario <math>L_{ik}<0</math>. | ||
* Como caso particular, los coeficientes de autoinducción <math>L_{kk}</math>, son siempre positivos. | * Como caso particular, los coeficientes de autoinducción <math>L_{kk}</math>, son siempre positivos. | ||
| - | == | + | ===Fuerza electromotriz=== |
| - | La inducción electromagnética se basa en que, a lo largo de una espira <math> | + | La inducción electromagnética se basa en que, a lo largo de una espira <math>C</math>, atravesada por un campo magnético cuyo flujo es variable en el tiempo, se induce una fuerza electromotriz (f.e.m.) dada por |
<center><math>\mathcal{E} = -\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}</math></center> | <center><math>\mathcal{E} = -\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}</math></center> | ||
| - | + | Si en lugar de una espira tenemos <math>N</math> espiras, rígidas y en una posición relativa fija, la f.e.m. que se induce en la espira <math>i</math> tendrá contribuciones de cada una de las espiras | |
| - | <center><math>\mathcal{E} = -\frac{\mathrm{d}\ }{\mathrm{d}t}\ | + | <center><math>\mathcal{E}_i = -\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\sum_k L_{ik}I_k\right)= -\sum_k L_{ik}\frac{\mathrm{d}I_k}{\mathrm{d}t}</math></center> |
| - | + | Esta fuerza electromotriz inducida habrá que añadirla a otras posibles fuentes, como generadores de tensión. | |
| - | Si | + | Si las espiras no son rígidas, hay que tener cuidado con la derivación. Un caso particular importante es el de un alternador. Si tenemos una bobina que gira en el campo magnético de otra, el coeficiente de inducción mutua no es constante, sino que oscila en el tiempo de forma aproximadamente sinusoidal |
| - | <center><math> | + | <center><math>M(t) = M_0\cos(\omega t)\,</math></center> |
| - | + | de forma que la fuerza electromotriz inducida en la bobina en reposo (el estátor) por la bobina giratoria (el rotor) cuando por esta circula una corriente continua es una función oscilante | |
| + | |||
| + | <center><math>\mathcal{E}_{21}=-\frac{\mathrm{d}\Phi_{21}}{\mathrm{d}t}=-\frac{\mathrm{d}\ }{\mathrm{d}t}(M_0I_0\cos(\omega t)) = M_0I_0\omega\, \mathrm{sen}(\omega t)</math></center> | ||
| + | |||
| + | Esta es la base de los generadores de corriente alterna. | ||
| - | ==Caso de dos espiras== | + | ===Caso de dos espiras=== |
Cuando solo tenemos dos espiras, el sistema se reduce a dos ecuaciones | Cuando solo tenemos dos espiras, el sistema se reduce a dos ecuaciones | ||
| Línea 89: | Línea 210: | ||
Cuando k es igual a la unidad (en valor absoluto) se dice que el acoplamiento es total. En ese caso todas las líneas de campo magnético que pasan por el interior de una espira, pasan también por el interior de la otra. | Cuando k es igual a la unidad (en valor absoluto) se dice que el acoplamiento es total. En ese caso todas las líneas de campo magnético que pasan por el interior de una espira, pasan también por el interior de la otra. | ||
| + | |||
| + | <center>[[Image:dosbobinas.png]]</center> | ||
| + | |||
| + | Así, en el caso de [[Autoinducción_e_inducción_mutua_de_bobinas|dos bobinas concéntricas]] las autoinducciones de cada bobina valen | ||
| + | |||
| + | <center><math>L_1 = \frac{\mu_0 N_1^2 \pi a^2}{h}\qquad\qquad L_2 = \frac{\mu_0 N_2^2 \pi b^2}{h}</math></center> | ||
| + | |||
| + | siendo <math>N_1</math> y <math>N_2</math> el numero de vueltas de la bobina interior y exterior, y <math>a</math> y <math>b</math> sus respectivos radios (<math>b>a</math>). | ||
| + | |||
| + | El coeficiente de inducción mutua en este caso vale | ||
| + | |||
| + | <center><math>M = \frac{\mu_0 N_1N_2 \pi a^2}{h}</math></center> | ||
| + | |||
| + | siendo el coeficiente de acoplamiento | ||
| + | |||
| + | <center><math>k = \frac{\mu_0 N_1N_2 \pi a^2}{\sqrt{\mu_0N_1^2\pi a^2/h}\sqrt{\mu_0N_2^2\pi b^2/h}}=\frac{a}{b}</math></center> | ||
| + | |||
| + | Esta cantidad es siempre menor que la unidad, pues <math>a < b</math>. | ||
| + | |||
| + | ==Transformador ideal== | ||
| + | Un modelo muy simplificado de transformador es un conjunto de dos bobinas del mismo radio pero diferente número de espiras y montadas de forma que su acoplamiento es total. Esto puede conseguirse montando una sobre otra o, lo más usual, las dos alrededor de un núcleo de hierro que conduce el flujo magnético provocando que las líneas de campo que pasan por una bobina lo hagan por la otra. | ||
| + | |||
| + | Si <math>\phi\,</math> es el flujo que atraviesa cada una de las espiras (el mismo en ambas bobinas), el flujo total en cada bobina será | ||
| + | |||
| + | <center><math>\Phi_1 = N_1\phi\qquad\qquad \Phi_2 = N_2\phi</math></center> | ||
| + | |||
| + | Si colocamos un voltímetro entre los bornes de cada bobina sus lecturas serán | ||
| + | |||
| + | <center><math>\Delta V_1 = \frac{\mathrm{d}\Phi_1}{\mathrm{d}t} = N_1\frac{\mathrm{d}\phi}{\mathrm{d}t} \qquad\qquad | ||
| + | \Delta V_2 = \frac{\mathrm{d}\Phi_1}{\mathrm{d}t} = N_2\frac{\mathrm{d}\phi}{\mathrm{d}t}</math></center> | ||
| + | |||
| + | y por tanto los dos voltajes son proporcionales | ||
| + | |||
| + | <center><math>\frac{\Delta V_2}{\Delta V_1}=\frac{N_2}{N_1}</math></center> | ||
| + | |||
| + | Esto quiere decir que si por la bobina 1 (el ''primario'') se establece un voltaje dependiente del tiempo <math>\Delta V_1</math>, en la bobina 2 (el “secundario”) aparece un voltaje <math>\Delta V_2</math>, relacionado por el anterior solo por la proporción entre los números de espiras. Es decir, que no depende de cómo varía la señal del primario con el tiempo, con tal de que no sea constante. Si el número de vueltas del secundario es superior al del primario, el voltaje del secundario será mayor en la misma proporción. Esto quiere decir que mediante este dispositivo se puede aumentar o reducir el voltaje a voluntad. Por ello, éste es un transformador ideal. | ||
| + | |||
| + | Podría parece que si se puede incrementar el voltaje, se puede “fabricar” energía de la nada. No es así. De la igualdad en los flujos magnéticos se puede demostrar que en un transformador ideal | ||
| + | |||
| + | <center><math>\frac{I_2}{I_1}=\frac{N_1}{N_2}</math></center> | ||
| + | |||
| + | es decir, que si el voltaje aumenta, la intensidad de corriente disminuye en la misma proporción, cumpliéndose | ||
| + | |||
| + | <center><math>P_\mathrm{in}=I_1\,\Delta V_1 = I_2\,\Delta V_2 = P_\mathrm{out}</math></center> | ||
| + | |||
| + | (en realidad sale menos de la que entra, porque siempre hay disipación por efecto Joule). | ||
| + | |||
| + | Podemos preguntarnos entonces por la utilidad de un transformador. Una importante es precisamente cambiar la intensidad de la corriente. Supongamos que tenemos una central eléctrica situada a 100km de una ciudad. Para llevar la energía eléctrica desde la central es necesario hacerla circular por un tendido eléctrico, en el cual se disipa energía por efecto Joule. Si la intensidad de corriente por este tendido es demasiado alta, las pérdidas pueden constituir una parte importante del total producido (y también hay que pagarlas). Por ello se emplea una serie de transformadores en la propia central para elevar la tensión al máximo posible. Se hace circular la corriente por un tendido de alta tensión y en la proximidad de la ciudad se vuelve a bajar la tensión a valores domésticos. Esto solo se puede hacer si la señal es variable en el tiempo, por lo que es necesario el uso de corriente alterna. | ||
[[Categoría:Inducción electromagnética (GIE)]] | [[Categoría:Inducción electromagnética (GIE)]] | ||
última version al 22:23 24 abr 2021
Contenido |
1 Autoinducción
1.1 Concepto
Cuando se tiene una espira cerrada por la cual circula una corriente variable en el tiempo, esa corriente produce un campo magnético (de acuerdo con la ley de Biot y Savart), el cual será también variable en el tiempo. Este campo tendrá un flujo magnético a través de la propia espira, y será también variable en el tiempo. De acuerdo con la ley de Faraday, un flujo magnético variable en el tiempo induce una fuerza electromotriz en la espira. Esta f.e.m. hay que añadirla a las otras que hubiera y por tanto modifica a la propia corriente.
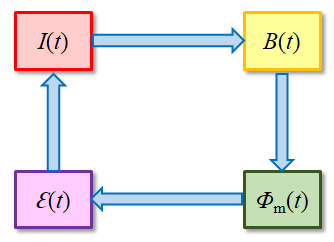
Por tanto, una corriente variable en el tiempo produce un efecto sobre sí misma, debido al campo magnético que genera. Este efecto se denomina autoinducción.
1.2 Coeficiente de autoinducción
El campo magnético debido a una corriente eléctrica, según la ley de Biot y Savart es proporcional a la intensidad de corriente que lo causa. Asimismo, este campo verifica la regla de la mano derecha respecto a la corriente.
Dada una curva cerrada C, el flujo magnético lo da la integral
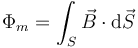
siendo S una superficie abierta apoyada en C y orientada según la regla de la mano derecha (es decir, en el mismo sentido que el campo magnético).
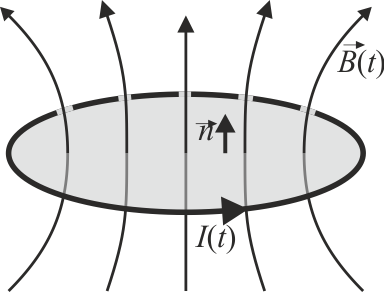
Al ser el campo proporcional a la intensidad de corriente, también lo será su flujo
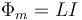
siendo L el denominado coeficiente de autoinducción, cuya unidad es el Henrio (H)
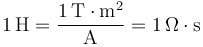
Por aplicación de la regla de la mano derecha, se llega a que este coeficiente es siempre positivo.
El coeficiente de autoinducción es una propiedad global del circuito. Sin embargo, dado a que a menudo el campo magnético es mucho más intenso en las bobinas presentes, puede considerarse que el flujo magnético se concentra en ellas y asignarle el valor de la autoinducción como algo localizado.
La fuerza electromotriz debida a la presencia de la autoinducción se calcula mediante la derivada
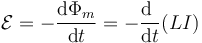
Si la espira es rígida (lo que es lo habitual), el coeficiente de autoinducción es constante y puede salir de la derivada, quedando el resultado más familiar
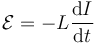
1.3 Comportamiento de un circuito
Supongamos una espira rígida caracterizada por una resistencia eléctrica R y un coeficiente de autoinducción L. Si esta espira se encuentra sometida a una fuera electromotriz externa (causada por un campo magnético aplicado, o por un generador), la ecuación para la corriente que pasa por el circuito es
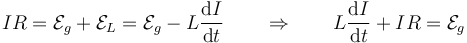
Podemos leer esta ecuación diferencial como que existe solo una fuente de tensión, 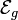 que alimenta a dos elementos en serie:
que alimenta a dos elementos en serie:
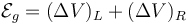
- Una resistencia R sin autoinducción, (ΔV)R = IR
- Una autoinducción L sin resistencia, (ΔV)L = L(dI / dt)´. que se representa con un nuevo símbolo
Así, lo que podría ser una simple anilla conductora sometida a un campo externo se modela por tres elementos de circuito. Nunca hay que olvidar que esto es un modelo. No tenemos una resistencia por un lado y una autoinducción por otro. Las dos propiedades van juntas en el mismo elemento real.
Este voltaje ΔVL es justamente el que mediría un voltímetro conectado a los extremos de una bobina ideal. Para ver por qué el signo es positivo y no negativo hay que clarificar el convenio de signos.
Supongamos un elemento de circuito, como puede ser un resistor, que tiene dos extremos A y B. Suponemos que la corriente es positiva si va de A a B (y negativa en caso contrario) Si ahora situamos un voltímetro puesto en paralelo entre los dos extremos tomamos la polaridad de forma que el voltímetro mide el voltaje
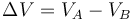
(si es necesario se indica con signos + en en lado de A y - en el de B). En este caso, para un resistor se cumple laey de Ohm
Obsérvese que si se cambia el criterio de signos para la corriente o para el voltaje, esta ley aparecería con signo cambiado.
Una expresión análoga se tiene para el caso de un condensador
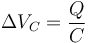
donde, para que el criterio de signos sea el correcto, Q representa la carga de la placa conectada a A.
Si ahora lo aplicamos a un generador observamos que, dado que la corriente en un generador entra por su polo negativo y sale por el positivo, se cumple
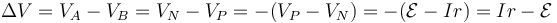
que podemos leer como una asociación en serie de una resistencia interna y una fuente ideal.
Si este caso lo particularizamos para una autoinducción
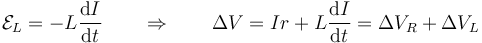
1.4 Corrientes de cierre y de ruptura
La presencia de la autoinducción afecta a la corriente que circula por el circuito.
Consideremos el caso particular de una señal escalón, es decir, que la fuente externa se conecta en t=0 cerrando el circuito y partir de ese momento tiene un valor 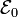 . Si no hubiera autoinducción, el efecto sería la aparición de una corriente continua de valor
. Si no hubiera autoinducción, el efecto sería la aparición de una corriente continua de valor
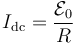
Debido a la autoinducción la conducta es un poco más complicada. Tenemos la ecuación
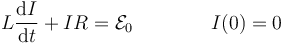
La segunda condición viene de que justo al cerrar el interruptor aun no circula corriente por la espira. La solución de esta ecuación diferencial es
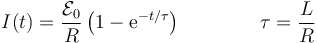
Esta solución nos dice que la corriente no se establece instantáneamente, sino que tiende exponencialmente a su valor estacionario. El tiempo que tarda es proporcional a τ = L / R, de forma que cuando ha pasado 4 o 5 veces el valor de tau ya se puede decir que la corriente ha llegado a su valor estacionario. El efecto de la autoinducción es entonces el de retardar este establecimiento. Como consecuencia de la ley de Lenz, la f.e.m. inducida se opone al cambio y retrasa su variación, tanto más cuanto mayor sea el coeficiente de autoinducción L.
Supongamos ahora el mismo circuito, con la misma fuente, en el que ha pasado el tiempo suficiente para que circule una corriente continua I0, si ahora cortocircuitamos el generador (es decir, lo mantenemos cerrado pero sin fuente externa que lo alimente), ¿desaparece instantáneamente la corriente? No. La ecuación diferencial para la corriente es ahora
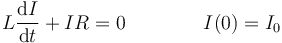
y su solución
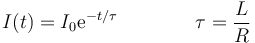
que quiere decir que la corriente tarda un tiempo del orden de tau en extinguirse. De nuevo, el efecto de la autoinducción es retrasar el cambio, manteniendo una corriente aunque ya no haya fuente externa que la produzca. Este efecto es transitorio y usualmente muy breve. Esta es la causa de que al desconectar un aparato salte una chispa. la autoinducción intenta mantener una corriente circulando por el circuito.
1.5 Caso de una bobina
El ejemplo más sencillo de autoinducción lo da una bobina cilíndrica de radio a, gran longitud h y número de espiras N. Cuando por ella pasa una intensidad de corriente I, el campo magnético que produce en su interior es aproximadamente
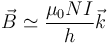
siendo  el unitario a lo largo del eje. El campo es nulo en su exterior. Para hallar el flujo de este campo a través de la propia bobina hay que tener en cuenta que el campo no atraviesa una sola espira, sino todas ellas, por lo que
el unitario a lo largo del eje. El campo es nulo en su exterior. Para hallar el flujo de este campo a través de la propia bobina hay que tener en cuenta que el campo no atraviesa una sola espira, sino todas ellas, por lo que
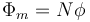
siendo  el flujo a través de una espira
el flujo a través de una espira
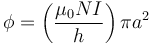
lo que nos da el coeficiente de autoinducción

Esta bobina también tiene una resistencia eléctrica, por tratarse de un hilo de cobre enrollado. Su valor es
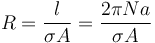
siendo A la sección transversal de cable (no de la bobina; esa es S).
1.6 Lectura de un voltímetro
Un voltímetro es un dispositivo que mide el voltaje (es decir, la integral del campo eléctrico), a lo largo del propio voltímetro. Si este aparato se halla en una región donde no hay campo magnético, esta medida coincide con la diferencia de potencial eléctrico.
Si tenemos una bobina, en la cual la corriente entra por su extremo A y sale por su extremo B, y colocamos un voltímetro entre sus extremos, la lectura que marca es
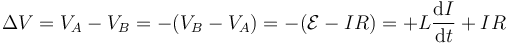
que de nuevo leemos como que tenemos dos elementos puestos en serie, aunque tengamos un solo elemento real.
2 Inducción mutua
2.1 Concepto
Si en lugar de una sola espira tenemos un conjunto de ellas, por las cuales circulan corrientes Ik, el flujo a través de una superficie Si apoyada en la espira i tendrá una contribución por cada una de las espiras
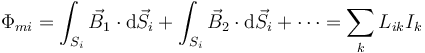
Las cantidades Lik para 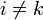 se denominan coeficientes de inducción mutua. Se miden asimismo en Henrios. Para i = k tenemos los coeficientes de autoinducción (del cual el sistema de una sola espira es un caso particular).
se denominan coeficientes de inducción mutua. Se miden asimismo en Henrios. Para i = k tenemos los coeficientes de autoinducción (del cual el sistema de una sola espira es un caso particular).
Los coeficientes de inducción mutua forman una matriz simétrica
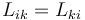
en la que los términos diagonales son siempre estrictamente positivos, mientras que los no diagonales pueden tener cualquier signo o ser nulos.
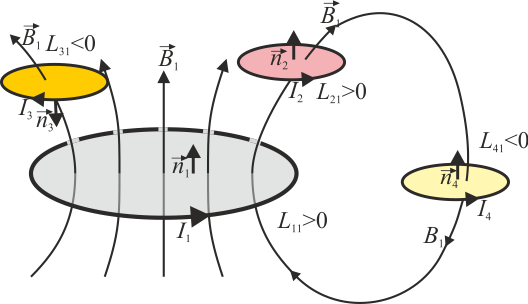
Para conocer el signo de cada coeficiente debe aplicarse el criterio siguiente:
- Para cada espira Ci se asigna un sentido de recorrido de la corriente.
- La regla de la mano derecha establece el sentido de la normal
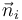 a la superficie Si apoyada en Ci.
a la superficie Si apoyada en Ci.
- El campo magnético producido por la espira Ck verifica asimismo la regla de la mano derecha respecto de la corriente que lo produce.
- El flujo del campo magnético es positivo si
 y
y 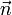 van el mismo sentido y negativo en caso contrario.
van el mismo sentido y negativo en caso contrario.
- Por tanto, si el campo
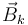 entra en la espira i según la orientación dada por la regla de la mano derecha para esta espira, Lik > 0. En caso contrario Lik < 0.
entra en la espira i según la orientación dada por la regla de la mano derecha para esta espira, Lik > 0. En caso contrario Lik < 0.
- Como caso particular, los coeficientes de autoinducción Lkk, son siempre positivos.
2.2 Fuerza electromotriz
La inducción electromagnética se basa en que, a lo largo de una espira C, atravesada por un campo magnético cuyo flujo es variable en el tiempo, se induce una fuerza electromotriz (f.e.m.) dada por
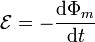
Si en lugar de una espira tenemos N espiras, rígidas y en una posición relativa fija, la f.e.m. que se induce en la espira i tendrá contribuciones de cada una de las espiras
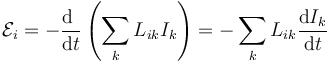
Esta fuerza electromotriz inducida habrá que añadirla a otras posibles fuentes, como generadores de tensión.
Si las espiras no son rígidas, hay que tener cuidado con la derivación. Un caso particular importante es el de un alternador. Si tenemos una bobina que gira en el campo magnético de otra, el coeficiente de inducción mutua no es constante, sino que oscila en el tiempo de forma aproximadamente sinusoidal
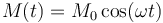
de forma que la fuerza electromotriz inducida en la bobina en reposo (el estátor) por la bobina giratoria (el rotor) cuando por esta circula una corriente continua es una función oscilante
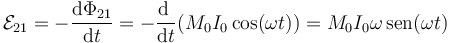
Esta es la base de los generadores de corriente alterna.
2.3 Caso de dos espiras
Cuando solo tenemos dos espiras, el sistema se reduce a dos ecuaciones
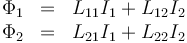
pero por las propiedades de simetría, esto se reduce a tres coeficientes
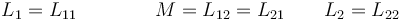
siendo L1 y L2 los coeficientes de autoinducción y M el único coeficiente de inducción mutua. A partir de ellos se define el coeficiente de acoplamiento
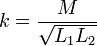
Puede demostrarse que k es un número menor que la unidad en valor absoluto.
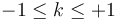
Cuando k es igual a la unidad (en valor absoluto) se dice que el acoplamiento es total. En ese caso todas las líneas de campo magnético que pasan por el interior de una espira, pasan también por el interior de la otra.
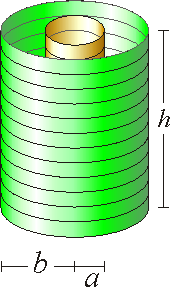
Así, en el caso de dos bobinas concéntricas las autoinducciones de cada bobina valen

siendo N1 y N2 el numero de vueltas de la bobina interior y exterior, y a y b sus respectivos radios (b > a).
El coeficiente de inducción mutua en este caso vale
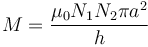
siendo el coeficiente de acoplamiento
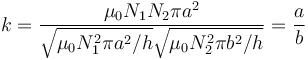
Esta cantidad es siempre menor que la unidad, pues a < b.
3 Transformador ideal
Un modelo muy simplificado de transformador es un conjunto de dos bobinas del mismo radio pero diferente número de espiras y montadas de forma que su acoplamiento es total. Esto puede conseguirse montando una sobre otra o, lo más usual, las dos alrededor de un núcleo de hierro que conduce el flujo magnético provocando que las líneas de campo que pasan por una bobina lo hagan por la otra.
Si  es el flujo que atraviesa cada una de las espiras (el mismo en ambas bobinas), el flujo total en cada bobina será
es el flujo que atraviesa cada una de las espiras (el mismo en ambas bobinas), el flujo total en cada bobina será

Si colocamos un voltímetro entre los bornes de cada bobina sus lecturas serán

y por tanto los dos voltajes son proporcionales
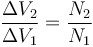
Esto quiere decir que si por la bobina 1 (el primario) se establece un voltaje dependiente del tiempo ΔV1, en la bobina 2 (el “secundario”) aparece un voltaje ΔV2, relacionado por el anterior solo por la proporción entre los números de espiras. Es decir, que no depende de cómo varía la señal del primario con el tiempo, con tal de que no sea constante. Si el número de vueltas del secundario es superior al del primario, el voltaje del secundario será mayor en la misma proporción. Esto quiere decir que mediante este dispositivo se puede aumentar o reducir el voltaje a voluntad. Por ello, éste es un transformador ideal.
Podría parece que si se puede incrementar el voltaje, se puede “fabricar” energía de la nada. No es así. De la igualdad en los flujos magnéticos se puede demostrar que en un transformador ideal
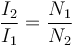
es decir, que si el voltaje aumenta, la intensidad de corriente disminuye en la misma proporción, cumpliéndose
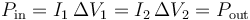
(en realidad sale menos de la que entra, porque siempre hay disipación por efecto Joule).
Podemos preguntarnos entonces por la utilidad de un transformador. Una importante es precisamente cambiar la intensidad de la corriente. Supongamos que tenemos una central eléctrica situada a 100km de una ciudad. Para llevar la energía eléctrica desde la central es necesario hacerla circular por un tendido eléctrico, en el cual se disipa energía por efecto Joule. Si la intensidad de corriente por este tendido es demasiado alta, las pérdidas pueden constituir una parte importante del total producido (y también hay que pagarlas). Por ello se emplea una serie de transformadores en la propia central para elevar la tensión al máximo posible. Se hace circular la corriente por un tendido de alta tensión y en la proximidad de la ciudad se vuelve a bajar la tensión a valores domésticos. Esto solo se puede hacer si la señal es variable en el tiempo, por lo que es necesario el uso de corriente alterna.





