Dilatación de un líquido en un recipiente

De Laplace

(Diferencias entre revisiones)

última version al 17:30 18 may 2013

1 Enunciado

Un líquido con un coeficiente de dilatación volumétrica $β$ llena por completo una estructura esférica de volumen $V 0$ a una temperatura $T 0$ . El material del que está hecho la esfera tiene un coeficiente medio de dilatación lineal $α$ . El líquido se puede expandir ocupando el tubo capilar de sección $A$ unido a la parte superior de la esfera. Si se produce una aumento de temperatura $Δ T$ , encuentre la expresión que da la altura $Δ h$ que sube el líquido en el capilar.

2 Solución

Al aumentar la temperatura en

Δ T

el nuevo volumen del líquido es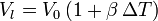

$V_l = V_0\,(1+\beta\,\Delta T)$

El recipiente también se dilata. El coeficiente medio de dilatación cúbica es 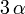$3\,\alpha$ . Por tanto el nuevo volumen es

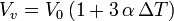
$V_v = V_0 \,(1+3\,\alpha\,\Delta T)$

El exceso de volumen del líquido es el que ocupa el capilar. Si la sección del capilar es $A 0$ la altura que sube el líquido es

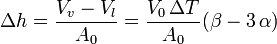
$\Delta h = \dfrac{V_v-V_l}{A_0} = \dfrac{V_0\,\Delta T}{A_0}(\beta-3\,\alpha)$

En general el coeficiente medio de dilatación cúbica de los líquidos es mayor que el de los sólidos. Suponiendo que el líquido es mercurio y el recipiente está hecho de vidrio tenemos

$\beta = 1.82\times10^{-4}\,\mathrm{K^{-1}} \qquad\qquad 3\alpha= 27\times10^{-6}\,\mathrm{K^{-1}}$

Por tanto $β - 3α > 0$ y el líquido sube por el capilar

2.1 Corrección teniendo en cuenta el aumento de la sección

Al aumentar la temperatura, la sección del capilar también aumenta. Como es una superficie, el coeficiente relevante es el coeficiente medio de dilatación superficial, que es igual a $2α$ , siendo $α$ el coeficiente de dilatación lineal. La sección es

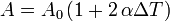
$A = A_0\,(1+2\,\alpha\Delta T)$

Entonces la altura que sube el líquido es

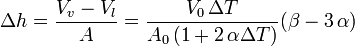
$\Delta h = \dfrac{V_v-V_l}{A} = \dfrac{V_0\,\Delta T}{A_0\,(1+2\,\alpha\Delta T)}(\beta-3\,\alpha)$

Ahora bien, si tenemos en cuenta que 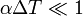$\alpha\Delta T\ll1$ podemos usar el desarrollo de Taylor de 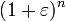$(1+\varepsilon)^n$ cuando 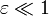$\varepsilon\ll1$ y obtenemos

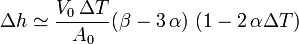
$\Delta h \simeq \dfrac{V_0\,\Delta T}{A_0}(\beta-3\,\alpha) \, \left(1- 2\,\alpha\Delta T \right)$

Al despreciar el segundo término del último paréntesis obtenemos la expresión anterior. Para una variación de temperatura 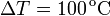$\Delta T=100\,\mathrm{^oC}$ el error relativo que se comete sería

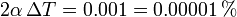
$2\alpha\,\Delta T = 0.001 = 0.00001\,%$

Como vemos, es muy pequeño, por lo que la expresión que obtuvimos en el apartado anterior es completamente válida.

@@ Línea 3: / Línea 3: @@
 == Solución==
-Al aumentar la temperatura en <math>\Delta T  </math> el nuevo volumen del líquido es
+[[Imagen:ejer_T1_4.gif|right]]Al aumentar la temperatura en <math>\Delta T  </math> el nuevo volumen del líquido es
 <center>
 <math>

Dilatación de un líquido en un recipiente

De Laplace

última version al 17:30 18 may 2013

1 Enunciado

2 Solución

2.1 Corrección teniendo en cuenta el aumento de la sección

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES