Fuerzas magnéticas (GIE)
De Laplace
(→Trabajo magnético nulo) |
m (→Par) |
||
| (23 ediciones intermedias no se muestran.) | |||
| Línea 22: | Línea 22: | ||
===Trabajo magnético nulo=== | ===Trabajo magnético nulo=== | ||
| - | Una propiedad característica de la fuerza magnética sobre una carga | + | Una propiedad característica de la fuerza magnética sobre una carga puntual es que no realiza trabajo, por ser siempre normal a la velocidad. |
<center><math>W = \int \vec{F}_m\cdot\mathrm{d}\vec{r}=\int(q\,\vec{v}\times\vec{B})\cdot(\vec{v}\,\mathrm{d}t)= q\int\vec{v}\cdot(\vec{v}\times\vec{B})\,\mathrm{d}t)=0</math></center> | <center><math>W = \int \vec{F}_m\cdot\mathrm{d}\vec{r}=\int(q\,\vec{v}\times\vec{B})\cdot(\vec{v}\,\mathrm{d}t)= q\int\vec{v}\cdot(\vec{v}\times\vec{B})\,\mathrm{d}t)=0</math></center> | ||
| Línea 43: | Línea 43: | ||
==Fuerza sobre una corriente lineal== | ==Fuerza sobre una corriente lineal== | ||
| + | En la naturaleza, raramente se presentan cargas puntuales individualmente. Lo habitual es que formen distribuciones de carga, con miles de millones de ellas en movimientos muy variados. En ese caso, la fuerza magnética sobre una distribución será la resultante de las fuerzas individuales | ||
| + | |||
| + | <center><math>\vec{F}=\sum_i q_i\left(\vec{v}_i\times\vec{B}(\vec{r}_i)\right)</math></center> | ||
| + | |||
| + | pero, como en otras ocasiones, este sumatorio no es nada útil, pues no conocemos, ni cuantas cargas hay, ni sus posiciones y velocidades. No obstante, podemos emplear esta expresión para deducir a partir de ellas expresiones más prácticas. | ||
| + | |||
| + | Cuando tenemos una corriente eléctrica, existe un movimiento neto de cargas, con una velocidad promedio en la dirección de la corriente. Si ésta se encuentra inmersa en un campo magnético, aparece una fuerza neta sobre la corriente, que sí puede ser medible. | ||
| + | |||
===Rectilínea=== | ===Rectilínea=== | ||
| + | Por simplificar el cálculo, supongamos un cable rectilíneo de longitud <math>l</math>, y sección transversal <math>S</math> por el cual circula una intensidad de corriente <math>I</math> y que este segmento se encuentra sumergido en un campo magnético uniforme <math>\vec{B}_0</math>. Entonces, en promedio, tenemos un flujo de cargas positivas avanzando a lo largo del hilo. Cada una de ellas experimenta una fuerza magnética perpendicular al campo y a la velocidad, es decir, perpendicular a la corriente. | ||
| + | |||
| + | El valor de la fuerza neta será el producto de la cantidad de carga en movimiento, por la velocidad promedio y por el campo magnético. Si consideramos un solo tipo de portadores de carga <math>Ze</math> (por ejemplo, para electrones, sería <math>Z = -1</math>), tales que hay N cargas por unidad de volumen, la carga total es | ||
| + | |||
| + | <center><math>Q= N(Ze)Sl\,</math></center> | ||
| + | |||
| + | y la fuerza neta | ||
| + | |||
| + | <center><math>\vec{F} = (N(Ze)Sl) \vec{v}\times \vec{B}</math></center> | ||
| + | |||
| + | pero | ||
| + | |||
| + | <center><math>I = JS = N(Ze)vS\,</math></center> | ||
| + | |||
| + | así que podemos expresar esta fuerza como | ||
| + | |||
| + | <center><math>\vec{F} = I(\Delta \vec{r})\times\vec{B}</math></center> | ||
| + | |||
| + | siendo <math>\Delta\vec{r}</math> el vector que va del inicio al final del segmento. | ||
| + | |||
| + | En el caso particular de que la corriente sea perpendicular al campo, si suponemos que el campo va en la dirección del eje Z, y la velocidad en la del eje Y nos queda | ||
| + | |||
| + | <center><math>\vec{B}_0=B_0\vec{k}\qquad\qquad \Delta\vec{r}=l\vec{\jmath}\qquad\Rightarrow\qquad \vec{F}=IlB_0\vec{\jmath}\times\vec{k}=IlB_0\vec{\imath}</math></center> | ||
| + | |||
===De forma arbitraria=== | ===De forma arbitraria=== | ||
| + | El cálculo anterior es demasiado simple para una situación general, en la que podemos tener una distribución cualquiera de corriente en un hilo de cualquier forma. Más en general, la fuerza sobre un elemento de corriente de longitud diferencial <math>\mathrm{d}\vec{r}</math> es | ||
| + | |||
| + | <center><math>\mathrm{d}\vec{F}=I\,\mathrm{d}\vec{r}\times\vec{B}</math></center> | ||
| + | |||
| + | siendo la fuerza total la suma de todos los diferenciales | ||
| + | |||
| + | <center><math>\vec{F}=I\int \mathrm{d}\vec{r}\times\vec{B}</math></center> | ||
| + | |||
| + | donde podemos sacar la intensidad de la integral, porque es constante a lo largo del cable. | ||
| + | <!-- | ||
| + | ===Espira sumergida totalmente en un campo=== | ||
| + | [[Imagen:espiratotal.gif|left|300px]] | ||
| + | |||
| + | Supongamos una espira cerrada por la que circula una corriente <math>I</math>, completamente inmersa en un campo magnético uniforme <math>\vec{B}_0</math>. ¿Cuánto vale la fuerza sobre la espira? | ||
| + | |||
| + | Al ser el campo uniforme, se puede extraer de la integral (¡ojo al orden!) | ||
| + | |||
| + | <center><math>\vec{F}_\vec{m}= I\oint_\Gamma \mathrm{d}\vec{r} \times \vec{B} = I\left( \oint_\Gamma \mathrm{d}\vec{r}\right) \times \vec{B}_0 = \vec{0}</math></center> | ||
| + | |||
| + | La integral sobre una curva cerrada de dr, es Δr, el desplazamiento entre el punto inicial y el final, que se anula para una curva cerrada. | ||
| + | |||
| + | ===Espira sumergida parcialmente en un campo=== | ||
| + | |||
| + | [[Imagen:espiraparcial.gif|left|300px]] | ||
| + | |||
| + | ¿Cuánto vale la fuerza sobre una espira cerrada, si ésta se encuentra sólo parcialmente dentro del campo magnético? | ||
| + | |||
| + | La integral se descompone en dos tramos | ||
| + | |||
| + | <center><math>\vec{F}_\mathrm{m} = I\oint_\Gamma \mathrm{d}\vec{r}\times\vec{B} = I\int_{\vec{r}_i}^{\vec{r}_f}\mathrm{d}\vec{r} \times \vec{B}_0 + I\int_{\vec{r}_f}^{\vec{r}_i}\mathrm{d}\vec{r} \times \vec{0} = I\left(\vec{r}_f-\vec{r}_i\right) \times \vec{B}_0</math></center> | ||
| + | |||
| + | El resultado sólo depende del desplazamiento entre el punto de entrada y de salida en el campo, no de la forma de la espira. | ||
| + | |||
| + | ===Fuerza sobre un segmento rectilíneo=== | ||
| + | |||
| + | Para el caso frecuente de un segmento rectilíneo de extremos <math>\vec{r}_i</math> y <math>\vec{r}_f</math>, inmerso en un campo magnético uniforme <math>\vec{B}_0</math>, la fuerza magnética se reduce a | ||
| + | |||
| + | <center><math>\vec{F}_\mathrm{m} = I\left(\vec{r}_f - \vec{r}_i\right) \times \vec{B}_0</math></center> | ||
| + | --> | ||
| + | |||
==Fuerza y par sobre una espira== | ==Fuerza y par sobre una espira== | ||
===Fuerza=== | ===Fuerza=== | ||
| + | Si tenemos una espira cerrada (un circuito) sumergida en un campo magnético, la fuerza sobre ella la da la integral cerrada | ||
| + | |||
| + | <center><math>\vec{F}=I\oint \mathrm{d}\vec{r}\times\vec{B}</math></center> | ||
| + | |||
| + | En general, esta integral no es nula, ya que el campo magnético depende de la posición. | ||
| + | |||
| + | En el caso particular de un campo magnético uniforme, <math>\vec{B}=\vec{B}_0</math>, el campo puede salir de la integral, aunque conservando el orden de los factores, por tratarse de un producto vectorial | ||
| + | |||
| + | <center><math>\vec{F}=I\oint \mathrm{d}\vec{r}\times\vec{B}_0=I\left(\oint \mathrm{d}\vec{r}\right)\times\vec{B}_0=\vec{0}</math></center> | ||
| + | |||
| + | La fuerza se anula porque la integral sobre una curva cerrada de una diferencial vale 0 (es igual a la diferencia entre su valor final e inicial, que son el mismo). | ||
| + | |||
| + | El que la fuerza neta sea nula no quiere decir que no se produzca acción alguna sobre la espira. De acuerdo con los teoremas para un sistema de partícula, esta anulación lo que implica es que el centro de masas de la espira no se acelera. Si inicialmente estaba en reposo, permanece en él. | ||
| + | |||
| + | Consideremos una espira cuadrada situada en un plano perpendicular a un campo magnético uniforme. Dependiendo del sentido de la corriente, sobre cada lada de la espira aparece una fuerza que va hacia el exterior o hacia el interior de la espira. Por tanto, aunque su centro no tiende a moverse, la espira tiende a deformarse, estirándose o encogiéndose. | ||
| + | |||
===Par=== | ===Par=== | ||
| - | == | + | Un caso particular importante, por su aplicación en máquinas eléctricas es el del par producido por un campo magnético sobre una espira de corriente. |
| + | |||
| + | Como modelo sencillo, consideremos el caso de una espira rectangular de lados <math>a</math> y <math>b</math>, inmersa en un campo magnético uniforme, similar al producido entre los polos de un imán. La espira no es perpendicular al campo magnético, sino que está inclinada respecto a él. | ||
| + | |||
| + | Para medir esta inclinación tomamos el ángulo <math>\alpha</math> formado por el campo magnético y el vector normal al plano de la espira <math>\vec{n}</math>, es decir que cuando <math>\alpha=0</math> la espira es completamente ortogonal al campo y si <math>\alpha = \pi/2</math> el campo magnético es paralelo al plano de la espira. | ||
| + | |||
| + | Sobre cada uno de los lados de la espira aparece una fuerza, que podemos situar en el centro de cada lado. La suma de estas cuatro fuerzas es nula. Sin embargo, sus direcciones no son coincidentes sino que se hallan sobre rectas paralelas. Por tanto aparece un par de fuerzas que tiende a rotar la espira. | ||
| + | |||
| + | <center>[[Archivo:par-magnetico.png]]</center> | ||
| + | |||
| + | Eso se ve más claro considerando un diagrama en el que la espira se encuentra de perfil, en el plano del campo magnético. Ahí se ve que la fuerza sobre el lado superior y sobre el inferior son iguales y opuestas, pero separadas una distancia que depende del tamaño de la espira y de su inclinación. Además de estas dos fuerzas hay fuerzas sobre los lados inclinados que, estas sí, se hallan sobre la misma recta, por lo que se anulan mutuamente. | ||
| + | |||
| + | El momento resultante puede calcularse según la fórmula general | ||
| + | |||
| + | <center><math>\vec{M}_O=\sum_i\vec{r}_i\times\vec{F}_i</math></center> | ||
| + | |||
| + | Su módulo es igual al producto de la fuerza del par multiplicado por la distancia entre las rectas soporte | ||
| + | |||
| + | <center><math>|\vec{M}_O| = |\vec{F}_1|d</math></center> | ||
| + | |||
| + | La fuerza sobre uno de los lados tiene por módulo | ||
| + | |||
| + | <center><math>|\vec{F}_1| = IbB_0</math></center> | ||
| + | |||
| + | y la distancia entre las rectas de acción de las fuerzas | ||
| + | |||
| + | <center><math>d = a\,\mathrm{sen}(\alpha)</math></center> | ||
| + | |||
| + | lo que da el módulo del momento del par de fuerzas | ||
| + | |||
| + | <center><math>|\vec{M}_O| = IabB_0\,\mathrm{sen}(\alpha)</math></center> | ||
| + | |||
| + | En forma vectorial, el vector momento puede escribirse como el producto vectorial | ||
| + | |||
| + | <center><math>\vec{M}_O = \vec{m}\times\vec{B}</math></center> | ||
| + | |||
| + | donde definimos el '''momento magnético''' (o momento dipolar magnético) de la espira como | ||
| + | |||
| + | <center><math>\vec{m}=IS\vec{n}\qquad\qquad S=ab</math></center> | ||
| + | |||
| + | siendo <math>\vec{n}</math> el vector normal al plano de la espira, orientado según la regla de la mano derecha respecto a la corriente. | ||
| + | |||
| + | El efecto de este par es alinear en dirección y sentido el vector momento magnético con el campo magnético aplicado. | ||
| + | |||
| + | Este es el principio subyacente a muchos motores eléctricos, en que mediante un campo magnético se hace girar una pieza. Para mantener una rotación constante, se hace cambiar el sentido del campo aplicado, de manera que el momento tenga que perseguir al campo continuadamente. | ||
| + | |||
| + | También es el principio de las brújulas. Un pequeño imán se comporta como un dipolo con momento magnético <math>\vec{m}</math>, con lo que al situarse en el interior de un campo magnético, se alinea con éste, marcando la dirección y en el sentido en que apunta. | ||
| + | |||
[[Categoría:Campo magnético (GIE)]] | [[Categoría:Campo magnético (GIE)]] | ||
última version al 19:57 21 mar 2017
Contenido |
1 Fuerza de Lorentz
1.1 Expresión
Según se ve en el tema de electrostática, la fuerza eléctrica sobre una carga puntual en reposo viene dada por
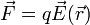
Sin embargo, si dicha carga se encuentra en movimiento, la experiencia muestra que se ve sometida a una fuerza adicional. Esta fuerza, que llamaremos fuerza magnética, verifica que es:
- Proporcional a la carga
- Proporcional al módulo de su velocidad
- Perpendicular a la velocidad
Con estas condiciones, la fuerza magnética debe ser de la forma
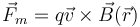
siendo  un nuevo campo, conocido como campo magnético. La fuerza total sobre una carga puntual es entonces
un nuevo campo, conocido como campo magnético. La fuerza total sobre una carga puntual es entonces
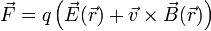
Esta expresión, que es válida en general, tanto para situaciones estáticas como dinámicas, se denomina Fuerza de Lorentz.
1.2 Trabajo magnético nulo
Una propiedad característica de la fuerza magnética sobre una carga puntual es que no realiza trabajo, por ser siempre normal a la velocidad.
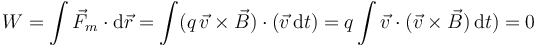
y por tanto permanece constante la energía cinética de una carga que se mueve en un campo magnético.
En términos de las componentes intrínsecas de la aceleración, tenemos que la fuerza es siempre normal a la velocidad y por tanto la aceleración tangencial es siempre nula
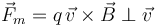

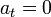
Si la aceleración tangencial es nula, la rapidez (módulo de la velocidad) permanece constante
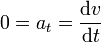

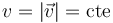
Una rapidez constante implica una energía cinética constante.
Esto quiere decir que una carga puntual que se mueve en el seno de un campo magnético podrá cambiar de dirección de la velocidad (esto es, su movimiento sí será acelerado), pero no se moverá ni más rápido ni más lento en ningún momento.
Hay que destacar que esta conclusión, que el campo magnético no realiza trabajo, es sólo cierta para una carga puntual sometida a la fuerza de Lorentz. Si tenemos una corriente eléctrica (formada por millones de partículas en movimiento) o un dipolo magnético (que también experimenta fuerzas magnéticas) no es cierto que la energía cinética permanezca constante. De hecho, los frenos magnéticos se basan en la disminución de la energía cinética por acción de un campo magnético.
2 Fuerza sobre una corriente lineal
En la naturaleza, raramente se presentan cargas puntuales individualmente. Lo habitual es que formen distribuciones de carga, con miles de millones de ellas en movimientos muy variados. En ese caso, la fuerza magnética sobre una distribución será la resultante de las fuerzas individuales
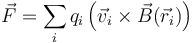
pero, como en otras ocasiones, este sumatorio no es nada útil, pues no conocemos, ni cuantas cargas hay, ni sus posiciones y velocidades. No obstante, podemos emplear esta expresión para deducir a partir de ellas expresiones más prácticas.
Cuando tenemos una corriente eléctrica, existe un movimiento neto de cargas, con una velocidad promedio en la dirección de la corriente. Si ésta se encuentra inmersa en un campo magnético, aparece una fuerza neta sobre la corriente, que sí puede ser medible.
2.1 Rectilínea
Por simplificar el cálculo, supongamos un cable rectilíneo de longitud l, y sección transversal S por el cual circula una intensidad de corriente I y que este segmento se encuentra sumergido en un campo magnético uniforme 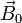 . Entonces, en promedio, tenemos un flujo de cargas positivas avanzando a lo largo del hilo. Cada una de ellas experimenta una fuerza magnética perpendicular al campo y a la velocidad, es decir, perpendicular a la corriente.
. Entonces, en promedio, tenemos un flujo de cargas positivas avanzando a lo largo del hilo. Cada una de ellas experimenta una fuerza magnética perpendicular al campo y a la velocidad, es decir, perpendicular a la corriente.
El valor de la fuerza neta será el producto de la cantidad de carga en movimiento, por la velocidad promedio y por el campo magnético. Si consideramos un solo tipo de portadores de carga Ze (por ejemplo, para electrones, sería Z = − 1), tales que hay N cargas por unidad de volumen, la carga total es
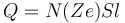
y la fuerza neta
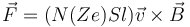
pero
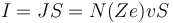
así que podemos expresar esta fuerza como
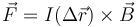
siendo 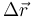 el vector que va del inicio al final del segmento.
el vector que va del inicio al final del segmento.
En el caso particular de que la corriente sea perpendicular al campo, si suponemos que el campo va en la dirección del eje Z, y la velocidad en la del eje Y nos queda
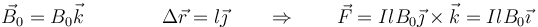
2.2 De forma arbitraria
El cálculo anterior es demasiado simple para una situación general, en la que podemos tener una distribución cualquiera de corriente en un hilo de cualquier forma. Más en general, la fuerza sobre un elemento de corriente de longitud diferencial 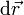 es
es
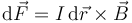
siendo la fuerza total la suma de todos los diferenciales
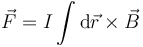
donde podemos sacar la intensidad de la integral, porque es constante a lo largo del cable.
3 Fuerza y par sobre una espira
3.1 Fuerza
Si tenemos una espira cerrada (un circuito) sumergida en un campo magnético, la fuerza sobre ella la da la integral cerrada
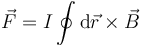
En general, esta integral no es nula, ya que el campo magnético depende de la posición.
En el caso particular de un campo magnético uniforme, 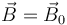 , el campo puede salir de la integral, aunque conservando el orden de los factores, por tratarse de un producto vectorial
, el campo puede salir de la integral, aunque conservando el orden de los factores, por tratarse de un producto vectorial

La fuerza se anula porque la integral sobre una curva cerrada de una diferencial vale 0 (es igual a la diferencia entre su valor final e inicial, que son el mismo).
El que la fuerza neta sea nula no quiere decir que no se produzca acción alguna sobre la espira. De acuerdo con los teoremas para un sistema de partícula, esta anulación lo que implica es que el centro de masas de la espira no se acelera. Si inicialmente estaba en reposo, permanece en él.
Consideremos una espira cuadrada situada en un plano perpendicular a un campo magnético uniforme. Dependiendo del sentido de la corriente, sobre cada lada de la espira aparece una fuerza que va hacia el exterior o hacia el interior de la espira. Por tanto, aunque su centro no tiende a moverse, la espira tiende a deformarse, estirándose o encogiéndose.
3.2 Par
Un caso particular importante, por su aplicación en máquinas eléctricas es el del par producido por un campo magnético sobre una espira de corriente.
Como modelo sencillo, consideremos el caso de una espira rectangular de lados a y b, inmersa en un campo magnético uniforme, similar al producido entre los polos de un imán. La espira no es perpendicular al campo magnético, sino que está inclinada respecto a él.
Para medir esta inclinación tomamos el ángulo α formado por el campo magnético y el vector normal al plano de la espira 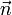 , es decir que cuando α = 0 la espira es completamente ortogonal al campo y si α = π / 2 el campo magnético es paralelo al plano de la espira.
, es decir que cuando α = 0 la espira es completamente ortogonal al campo y si α = π / 2 el campo magnético es paralelo al plano de la espira.
Sobre cada uno de los lados de la espira aparece una fuerza, que podemos situar en el centro de cada lado. La suma de estas cuatro fuerzas es nula. Sin embargo, sus direcciones no son coincidentes sino que se hallan sobre rectas paralelas. Por tanto aparece un par de fuerzas que tiende a rotar la espira.
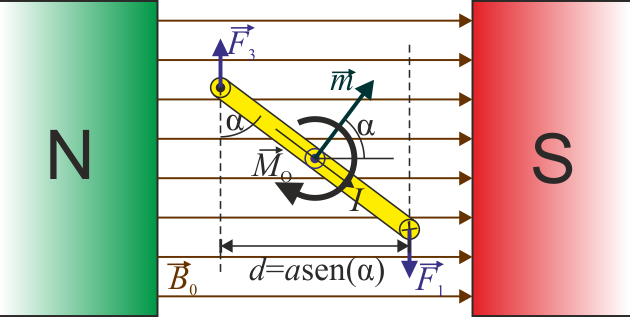
Eso se ve más claro considerando un diagrama en el que la espira se encuentra de perfil, en el plano del campo magnético. Ahí se ve que la fuerza sobre el lado superior y sobre el inferior son iguales y opuestas, pero separadas una distancia que depende del tamaño de la espira y de su inclinación. Además de estas dos fuerzas hay fuerzas sobre los lados inclinados que, estas sí, se hallan sobre la misma recta, por lo que se anulan mutuamente.
El momento resultante puede calcularse según la fórmula general
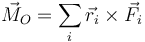
Su módulo es igual al producto de la fuerza del par multiplicado por la distancia entre las rectas soporte
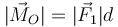
La fuerza sobre uno de los lados tiene por módulo
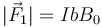
y la distancia entre las rectas de acción de las fuerzas
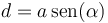
lo que da el módulo del momento del par de fuerzas
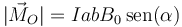
En forma vectorial, el vector momento puede escribirse como el producto vectorial
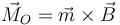
donde definimos el momento magnético (o momento dipolar magnético) de la espira como

siendo 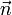 el vector normal al plano de la espira, orientado según la regla de la mano derecha respecto a la corriente.
el vector normal al plano de la espira, orientado según la regla de la mano derecha respecto a la corriente.
El efecto de este par es alinear en dirección y sentido el vector momento magnético con el campo magnético aplicado.
Este es el principio subyacente a muchos motores eléctricos, en que mediante un campo magnético se hace girar una pieza. Para mantener una rotación constante, se hace cambiar el sentido del campo aplicado, de manera que el momento tenga que perseguir al campo continuadamente.
También es el principio de las brújulas. Un pequeño imán se comporta como un dipolo con momento magnético 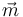 , con lo que al situarse en el interior de un campo magnético, se alinea con éste, marcando la dirección y en el sentido en que apunta.
, con lo que al situarse en el interior de un campo magnético, se alinea con éste, marcando la dirección y en el sentido en que apunta.





