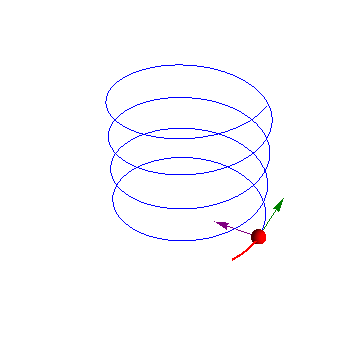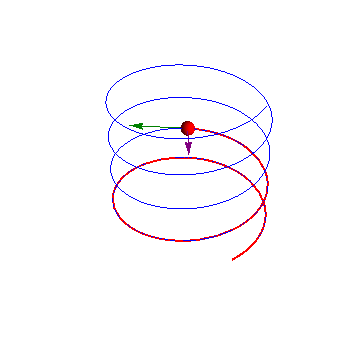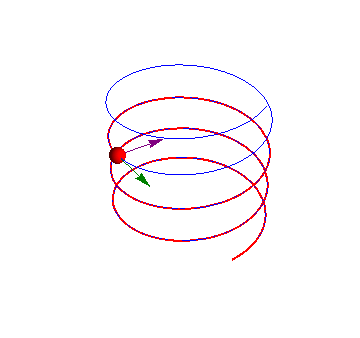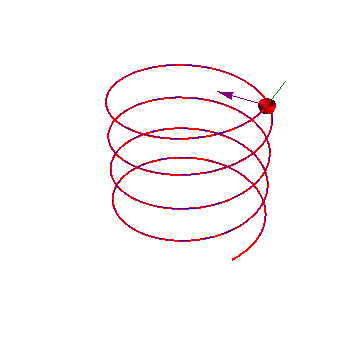
Ejemplo de movimiento helicoidal (GIE)
De Laplace
(→Velocidad) |
(→Radio de curvatura) |
||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 11: | Línea 11: | ||
# Determine la velocidad en cada punto expresada en la base de coordenadas cilíndricas. | # Determine la velocidad en cada punto expresada en la base de coordenadas cilíndricas. | ||
| - | # Determine las ecuaciones horarias <math>\rho=\rho(t)</math>, <math>\ | + | # Determine las ecuaciones horarias <math>\rho=\rho(t)</math>, <math>\theta=\theta(t)</math> y <math>z=z(t)</math>. ¿Cuánto vale el ''paso de rosca'' de la hélice, esto es, lo que sube en el tiempo que da una vuelta alrededor del eje? |
# Calcule la aceleración del movimiento, así como sus componentes intrínsecas en cada punto del movimiento. | # Calcule la aceleración del movimiento, así como sus componentes intrínsecas en cada punto del movimiento. | ||
# Determine el radio de curvatura de la trayectoria en cualquier instante. | # Determine el radio de curvatura de la trayectoria en cualquier instante. | ||
| Línea 29: | Línea 29: | ||
La base asociada a las coordenadas cilíndricas forma un triedro ortonormal y dextrógiro, por lo que cumple | La base asociada a las coordenadas cilíndricas forma un triedro ortonormal y dextrógiro, por lo que cumple | ||
| - | <center><math>\vec{k}\times\vec{u}_\rho=\vec{u}_\ | + | <center><math>\vec{k}\times\vec{u}_\rho=\vec{u}_\theta</math></center> |
y queda la velocidad | y queda la velocidad | ||
| - | <center><math>\vec{v}=\omega_0\rho\vec{u}_\ | + | <center><math>\vec{v}=\omega_0\rho\vec{u}_\theta+v_0\vec{k}</math></center> |
Vemos que posee una componente acimutal (correspondiente al giro) y una vertical, asociada a la ascensión. | Vemos que posee una componente acimutal (correspondiente al giro) y una vertical, asociada a la ascensión. | ||
| Línea 40: | Línea 40: | ||
Por otra parte, la velocidad de una partícula, expresada en coordenadas cilíndricas, es | Por otra parte, la velocidad de una partícula, expresada en coordenadas cilíndricas, es | ||
| - | <center><math>\vec{v}=\dot{\rho}\vec{u}_\rho + \rho\dot{\ | + | <center><math>\vec{v}=\dot{\rho}\vec{u}_\rho + \rho\dot{\theta}\vec{u}_\theta+\dot{z}\vec{k}</math></center> |
Igualando componente a componente, nos quedan las igualdades | Igualando componente a componente, nos quedan las igualdades | ||
| - | <center><math>\dot{\rho} = 0\qquad \rho\dot{\ | + | <center><math>\dot{\rho} = 0\qquad \rho\dot{\theta}=\omega_0\rho\qquad\dot{z}=v_0</math></center> |
La integración de estas tres ecuaciones es inmediata, ya que cada una de las derivadas es una constante o nula. | La integración de estas tres ecuaciones es inmediata, ya que cada una de las derivadas es una constante o nula. | ||
| - | <center><math>\rho=\rho_0\qquad\ | + | <center><math>\rho=\rho_0\qquad\theta=\omega_0t + \theta_0\qquad z=v_0t+z_0</math></center> |
Los valores de las constantes de integración los obtenemos de la posición inicial. sabemos que en <math>t=0</math> la partícula se encuentra en | Los valores de las constantes de integración los obtenemos de la posición inicial. sabemos que en <math>t=0</math> la partícula se encuentra en | ||
| Línea 56: | Línea 56: | ||
que corresponde a las coordenadas cilíndricas | que corresponde a las coordenadas cilíndricas | ||
| - | <center><math>\rho_0 = A\qquad\ | + | <center><math>\rho_0 = A\qquad\theta_0 = 0\qquad z_0=0</math></center> |
por tanto las ecuaciones horarias del movimiento son | por tanto las ecuaciones horarias del movimiento son | ||
| - | <center><math>\rho=A\qquad\ | + | <center><math>\rho=A\qquad\theta=\omega_0t\qquad z=v_0t</math></center> |
En coordenadas cartesianas, estas ecuaciones horarias quedan | En coordenadas cartesianas, estas ecuaciones horarias quedan | ||
| - | <center><math>x = \rho \cos(\ | + | <center><math>x = \rho \cos(\theta) = A\cos(\omega_0t)\qquad y = \rho\,\mathrm{sen}(\theta) = A\,\mathrm{sen}(\omega_0t)\qquad z = v_0t</math></center> |
==Aceleración== | ==Aceleración== | ||
| Línea 74: | Línea 74: | ||
o la correspondiente en cilíndricas | o la correspondiente en cilíndricas | ||
| - | <center><math>\vec{a} = (\ddot{ | + | <center><math>\vec{a} = (\ddot{\rho}-\rho\,\dot{\theta}^2)\,\vec{u}_{\rho} + (2\dot{\rho}\,\dot{\theta}+\rho\ddot{\theta})\,\vec{u}_{\theta}+\ddot{z}\vec{k}</math></center> |
Para aplicar esta última, hallamos las segundas derivadas, | Para aplicar esta última, hallamos las segundas derivadas, | ||
| - | <center><math>\ddot{\rho}=0\qquad\ddot{\ | + | <center><math>\ddot{\rho}=0\qquad\ddot{\theta}=0\qquad\ddot{z}=0</math></center> |
y la aceleración se reduce a | y la aceleración se reduce a | ||
| Línea 85: | Línea 85: | ||
Resulta una aceleración puramente radial y hacia adentro. | Resulta una aceleración puramente radial y hacia adentro. | ||
| + | |||
===Aceleración tangencial=== | ===Aceleración tangencial=== | ||
[[Archivo:movimiento-helicoidal.gif|right]] | [[Archivo:movimiento-helicoidal.gif|right]] | ||
| Línea 90: | Línea 91: | ||
La aceleración que acabamos de hallar es puramente ortogonal a la velocidad, ya que una es radial, mientras que la otra posee solo componentes acimutal y vertical | La aceleración que acabamos de hallar es puramente ortogonal a la velocidad, ya que una es radial, mientras que la otra posee solo componentes acimutal y vertical | ||
| - | <center><math>\vec{a}\cdot\vec{v}=\left(-\omega_0^2A\vec{u}_\rho\right)\cdot\left(\omega_0\rho\vec{u}_\ | + | <center><math>\vec{a}\cdot\vec{v}=\left(-\omega_0^2A\vec{u}_\rho\right)\cdot\left(\omega_0\rho\vec{u}_\theta+v_0\vec{k}\right) = 0</math></center> |
Por tanto, la aceleración tangencial es nula | Por tanto, la aceleración tangencial es nula | ||
| Línea 114: | Línea 115: | ||
<center><math>R = \frac{|\vec{v}|^2}{a_n}=\frac{\omega_0^2A^2+v_0^2}{\omega_0^2A}=A+\frac{v_0^2}{\omega_0^2A}</math></center> | <center><math>R = \frac{|\vec{v}|^2}{a_n}=\frac{\omega_0^2A^2+v_0^2}{\omega_0^2A}=A+\frac{v_0^2}{\omega_0^2A}</math></center> | ||
| - | Resulta un radio de curvatura mayor que el radio de la hélice (que vale A) ya que una hélice viene a ser | + | Resulta un radio de curvatura mayor que el radio de la hélice (que vale A) ya que una hélice viene a ser un arco circular que se estira verticalmente. |
[[Categoría:Problemas de cinemática de la partícula (GIE)]] | [[Categoría:Problemas de cinemática de la partícula (GIE)]] | ||
[[Categoría:Problemas de cinemática tridimensional (GIE)]] | [[Categoría:Problemas de cinemática tridimensional (GIE)]] | ||
última version al 19:13 28 oct 2016
Contenido |
1 Enunciado
El movimiento de un pájaro en una corriente térmica es aproximadamente helicoidal, compuesto de un movimiento ascensional y uno de giro alrededor del eje de subida, de forma que la velocidad en cada punto de la trayectoria puede escribirse como
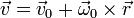
siendo

dos vectores constantes. Si la posición inicial es 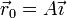
- Determine la velocidad en cada punto expresada en la base de coordenadas cilíndricas.
- Determine las ecuaciones horarias ρ = ρ(t), θ = θ(t) y z = z(t). ¿Cuánto vale el paso de rosca de la hélice, esto es, lo que sube en el tiempo que da una vuelta alrededor del eje?
- Calcule la aceleración del movimiento, así como sus componentes intrínsecas en cada punto del movimiento.
- Determine el radio de curvatura de la trayectoria en cualquier instante.
2 Velocidad
La velocidad en cada punto la obtenemos simplemente sustituyendo en la expresión indicada
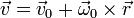
donde  es el vector de posición del pájaro, que en coordenadas cilíndricas se expresa
es el vector de posición del pájaro, que en coordenadas cilíndricas se expresa
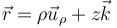
Sustituyendo nos queda
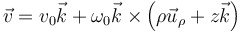
La base asociada a las coordenadas cilíndricas forma un triedro ortonormal y dextrógiro, por lo que cumple
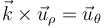
y queda la velocidad
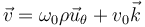
Vemos que posee una componente acimutal (correspondiente al giro) y una vertical, asociada a la ascensión.
3 Ecuaciones horarias
Por otra parte, la velocidad de una partícula, expresada en coordenadas cilíndricas, es
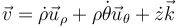
Igualando componente a componente, nos quedan las igualdades
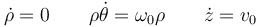
La integración de estas tres ecuaciones es inmediata, ya que cada una de las derivadas es una constante o nula.
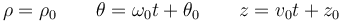
Los valores de las constantes de integración los obtenemos de la posición inicial. sabemos que en t = 0 la partícula se encuentra en
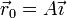
que corresponde a las coordenadas cilíndricas
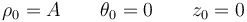
por tanto las ecuaciones horarias del movimiento son
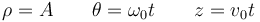
En coordenadas cartesianas, estas ecuaciones horarias quedan
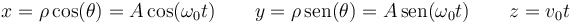
4 Aceleración
4.1 Vector aceleración
Podemos hallar la aceleración a partir de su expresión en cartesianas
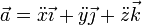
o la correspondiente en cilíndricas
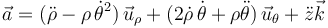
Para aplicar esta última, hallamos las segundas derivadas,
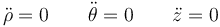
y la aceleración se reduce a
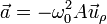
Resulta una aceleración puramente radial y hacia adentro.
4.2 Aceleración tangencial
La aceleración que acabamos de hallar es puramente ortogonal a la velocidad, ya que una es radial, mientras que la otra posee solo componentes acimutal y vertical
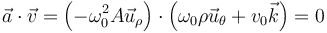
Por tanto, la aceleración tangencial es nula
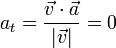
Esto nos dice también que el movimiento es uniforme y la celeridad es constante
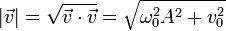
4.3 Aceleración normal
Si la aceleración tangencial es nula, toda la aceleración es normal
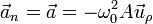
y, en forma escalar,
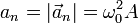
5 Radio de curvatura
Una vez que tenemos la aceleración normal y la rapidez, el radio de curvatura es inmediato
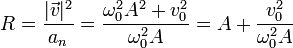
Resulta un radio de curvatura mayor que el radio de la hélice (que vale A) ya que una hélice viene a ser un arco circular que se estira verticalmente.