Asociación de dos máquinas térmicas
De Laplace
(→Máquinas reales) |
(→Máquinas ideales) |
||
| (Una edición intermedia no se muestra.) | |||
| Línea 14: | Línea 14: | ||
Al tratarse de máquinas de Carnot ideales, la primera máquina produce un trabajo por unidad de tiempo | Al tratarse de máquinas de Carnot ideales, la primera máquina produce un trabajo por unidad de tiempo | ||
| - | <center><math>\dot{W}_\mathrm{out1} = \eta_1\,\dot{Q}_\mathrm{in1} = \left(1-\frac{T_M}{T_C}\right)\dot{Q}_\mathrm{in1}</math></center> | + | <center><math>\dot{W}_\mathrm{out1} = \eta_1^\mathrm{rev}\,\dot{Q}_\mathrm{in1} = \left(1-\frac{T_M}{T_C}\right)\dot{Q}_\mathrm{in1}</math></center> |
que numéricamente tiene el valor | que numéricamente tiene el valor | ||
| Línea 34: | Línea 34: | ||
La potencia desarrollada por la segunda máquina la da su rendimiento | La potencia desarrollada por la segunda máquina la da su rendimiento | ||
| - | <center><math>\dot{W}_\mathrm{out2} = \eta_2 \dot{Q}_\mathrm{in2}= \left(1-\frac{T_F}{T_M}\right)\frac{T_M}{T_C}\dot{Q}_\mathrm{in1}=\left(\frac{T_M}{T_C}-\frac{T_F}{T_C}\right)\dot{Q}_\mathrm{in1}</math></center> | + | <center><math>\dot{W}_\mathrm{out2} = \eta_2^\mathrm{rev} \dot{Q}_\mathrm{in2}= \left(1-\frac{T_F}{T_M}\right)\frac{T_M}{T_C}\dot{Q}_\mathrm{in1}=\left(\frac{T_M}{T_C}-\frac{T_F}{T_C}\right)\dot{Q}_\mathrm{in1}</math></center> |
con el valor numérico | con el valor numérico | ||
| Línea 40: | Línea 40: | ||
<center><math>\dot{W}_\mathrm{out2}=\left(1-\frac{300}{600}\right)384\,\mathrm{W} = 192\,\mathrm{W}</math></center> | <center><math>\dot{W}_\mathrm{out2}=\left(1-\frac{300}{600}\right)384\,\mathrm{W} = 192\,\mathrm{W}</math></center> | ||
| - | El flujo calor desechado por la segunda máquina es | + | El flujo de calor desechado por la segunda máquina es |
<center><math>\dot{Q}_\mathrm{out2}=\dot{Q}_\mathrm{in2}-\dot{W}_\mathrm{out2}=\frac{T_F}{T_M}\dot{Q}_\mathrm{in2}=\frac{T_F}{T_M}\,\frac{T_M}{T_C}\dot{Q}_\mathrm{in1}=\frac{T_F}{T_C}\dot{Q}_\mathrm{in1}</math></center> | <center><math>\dot{Q}_\mathrm{out2}=\dot{Q}_\mathrm{in2}-\dot{W}_\mathrm{out2}=\frac{T_F}{T_M}\dot{Q}_\mathrm{in2}=\frac{T_F}{T_M}\,\frac{T_M}{T_C}\dot{Q}_\mathrm{in1}=\frac{T_F}{T_C}\dot{Q}_\mathrm{in1}</math></center> | ||
última version al 18:16 3 abr 2014
Contenido |
1 Enunciado
Se tiene una máquina de Carnot que opera entre 1500 K y 600 K recibiendo un flujo de calor 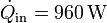 . El calor que sale de ella no se desperdicia sino que se usa para alimentar una segunda máquina de Carnot que opera entre 600 K y 300 K. Halle el rendimiento del conjunto, el calor que sale del sistema y el trabajo total que realiza en la unidad de tiempo.
. El calor que sale de ella no se desperdicia sino que se usa para alimentar una segunda máquina de Carnot que opera entre 600 K y 300 K. Halle el rendimiento del conjunto, el calor que sale del sistema y el trabajo total que realiza en la unidad de tiempo.
Supongamos ahora que en lugar de tratarse de máquinas de Carnot se trata de máquinas reales que tienen un rendimiento del 50\% del máximo posible. ¿Cuál sería en ese caso el rendimiento de la asociación, el calor desechado y el trabajo total realizado? ¿Cuánta entropía se produce a lo largo de un ciclo de la máquina?
2 Máquinas ideales
Consideramos los tres focos térmicos con las temperaturas

Al tratarse de máquinas de Carnot ideales, la primera máquina produce un trabajo por unidad de tiempo
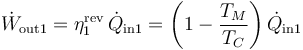
que numéricamente tiene el valor
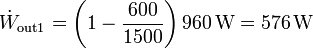
El flujo de calor desechado por esta máquina es

con el valor

Este calor de desecho es el que se usa para alimentar la segunda máquina
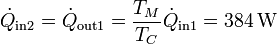
La potencia desarrollada por la segunda máquina la da su rendimiento
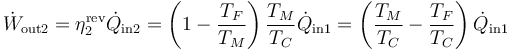
con el valor numérico
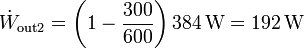
El flujo de calor desechado por la segunda máquina es
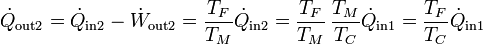
con valor
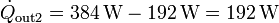
La potencia total desarrollada por el sistema es la suma de las dos individuales

Vemos que el resultado es exactamente el mismo que el que resultaría de una sola máquina de Carnot que operara entre las dos temperaturas extremas. Esto es así, porque al ser cada una de ellas reversible, el conjunto también lo es. Todas las máquinas reversibles que operan entre las mismas temperaturas tienen el mismo rendimiento por lo que el resultado debe ser el indicado.
El valor numérico de la potencia total es
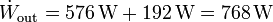
y el rendimiento de la asociación
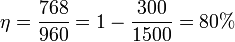
3 Máquinas reales
En el segundo caso tenemos máquinas con un rendimiento inferior al ideal. Nos dan el rendimiento relativo al máximo, o rendimiento de la segunda ley. Para la primera máquina
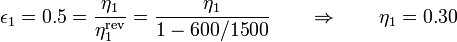
y para la segunda
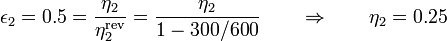
La potencia desarrollada por la primera máquina es ahora la mitad de la máxima
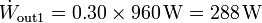
mientras que el calor desechado por segundo aumenta
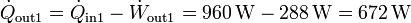
Este calor se entra como entrada para la segunda máquina, que produce una potencia

y desecha un flujo de calor
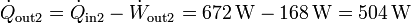
La potencia total desarrollada vale
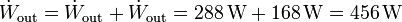
Siendo el rendimiento
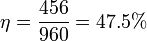
El rendimiento de la segunda ley para la asociación es
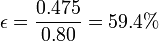
es decir, es mayor que el de cada una de las máquinas por separado. La razón es que mientras la primera máquina produce ahora la mitad de trabajo que la ideal, la segunda produce más (un 87.5%) porque le entra más calor que antes.
4 Producción de entropía
4.1 Máquinas de Carnot reversibles
En el primer caso, las máquinas son perfectamente reversibles y la producción de entropía en cada una de ellas es nula.
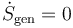
4.2 Máquinas reales
En el segundo caso, las máquinas no realizan todo el trabajo posible y ello va unido a la producción de entropía por ellas.
La entropía producida por una máquina térmica que opera entre dos focos es
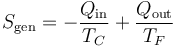
Una expresión análoga se cumple si consideramos la producción de entropía por segundo
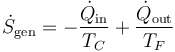
Para la máquina superior, esta fórmula nos da
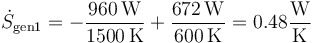
y para la inferior
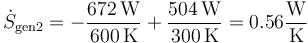
Sumando las dos contribuciones, la producción de entropía por segundo es

Vemos que el término intermedio se cancela, ya que la entropía que expulsa una máquina es absorbida por la otra. Podríamos haber calculado la producción de entropía directamente como