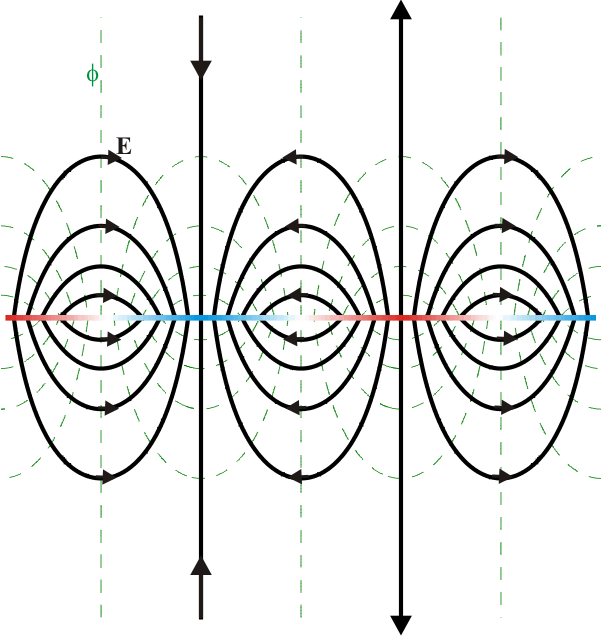
Campo y carga de un potencial conocido
De Laplace
(→Campo eléctrico) |
(→Superficial) |
||
| (6 ediciones intermedias no se muestran.) | |||
| Línea 11: | Línea 11: | ||
==Solución== | ==Solución== | ||
===Campo eléctrico=== | ===Campo eléctrico=== | ||
| - | Para calcular el campo debemos | + | Para calcular el campo debemos hallar el gradiente del potencial, cambiado de signo. |
<center><math>\mathbf{E}=-\nabla\phi\,</math></center> | <center><math>\mathbf{E}=-\nabla\phi\,</math></center> | ||
| Línea 17: | Línea 17: | ||
Para esto es conveniente separa el potencial en dos regiones | Para esto es conveniente separa el potencial en dos regiones | ||
| - | <center><math>\phi = \begin{cases}V_0 \mathrm{e}^ | + | <center><math>\phi = \begin{cases}V_0 \mathrm{e}^{ky}\cos(kx) & y < 0 \\ & \\ V_0 \mathrm{e}^{-ky}\cos(kx) & y > 0 \end{cases}</math></center> |
Hallando ahora el gradiente en cada región tenemos, | Hallando ahora el gradiente en cada región tenemos, | ||
<center> | <center> | ||
<math>\mathbf{E}=-\frac{\partial\phi}{\partial x}\mathbf{u}_x-\frac{\partial\phi}{\partial y}\mathbf{u}_y= | <math>\mathbf{E}=-\frac{\partial\phi}{\partial x}\mathbf{u}_x-\frac{\partial\phi}{\partial y}\mathbf{u}_y= | ||
| - | \begin{cases} | + | \begin{cases}V_0k\mathrm{e}^{ky}\left(\mathrm{sen}(kx)\mathbf{u}_x-\cos(kx)\mathbf{u}_y\right) & y < 0 \\ & \\ |
| - | + | V_0k\mathrm{e}^{-ky}\left(\mathrm{sen}(kx)\mathbf{u}_x+\cos(kx)\mathbf{u}_y\right) & y > 0\end{cases}</math></center> | |
| + | |||
| + | o, agrupando los dos casos | ||
| + | |||
| + | <center><math>\mathbf{E}=V_0k\mathrm{e}^{-k|y|}\left(\mathrm{sen}(kx)\mathbf{u}_x+\sgn(y)\cos(kx)\mathbf{u}_y\right)</math> | ||
| + | </center> | ||
===Densidad de carga=== | ===Densidad de carga=== | ||
| + | ====Volumétrica==== | ||
| + | La densidad de carga de volumen la obtenemos por aplicación de la ley de Gauss en forma diferencial | ||
| + | |||
| + | <center><math>\rho = \varepsilon_0 \nabla\cdot \mathbf{E} = \varepsilon_0\left(\frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}+\frac{\partial E_z}{\partial y}\right)</math></center> | ||
| + | |||
| + | Para hallar esta cantidad volvemos a descomponer en los dos semiespacios. Para <math>y > 0</math> tenemos | ||
| + | |||
| + | <center><math>\mathbf{E} = V_0k\left(\mathrm{e}^{-ky}\mathrm{sen}(kx)\mathbf{u}_x+\mathrm{e}^{-ky}\cos(kx)\mathbf{u}_y\right)</math></center> | ||
| + | |||
| + | |||
| + | <center><math>\rho = \varepsilon_0 V_0 k \left(k\mathrm{e}^{-ky}\cos(kx)-k\mathrm{e}^{-ky}\cos(kx)\right) = 0</math></center> | ||
| + | |||
| + | y para <math>y < 0</math> | ||
| + | |||
| + | <center><math>\mathbf{E} = V_0k\left(\mathrm{e}^{ky}\mathrm{sen}(kx)\mathbf{u}_x-\mathrm{e}^{ky}\cos(kx)\mathbf{u}_y\right)</math></center> | ||
| + | |||
| + | |||
| + | <center><math>\rho = \varepsilon_0 V_0 k \left(k\mathrm{e}^{ky}\cos(kx)-k\mathrm{e}^{ky}\cos(kx)\right) = 0</math></center> | ||
| + | |||
| + | Por tanto, la densidad de carga de volumen es nula en todos los puntos del espacio. Puesto que el campo no es nulo, y además se anula en el infinito, es claro que debe haber alguna densidad de carga adicional. Esta densidad es la superficial, que se encuentra en las superficies donde el campo es discontinuo. | ||
| + | |||
| + | ====Superficial==== | ||
| + | La densidad de carga superficial sólo puede estar presente en las superficies de discontinuidad, siendo su valor | ||
| + | |||
| + | <center><math>\sigma_s = \varepsilon_0 \mathbf{n}\cdot\left[\mathbf{E}\right]</math></center> | ||
| + | |||
| + | En nuestro caso, el único salto en el campo eléctrico se da en <math>y=0</math>, a cuyos lados el campo vale | ||
| + | |||
| + | <center><math>\mathbf{E}(y=0^+) = V_0k\left(\mathrm{sen}(kx)\mathbf{u}_x+\cos(kx)\mathbf{u}_y\right)</math></center> | ||
| + | |||
| + | <center><math>\mathbf{E}(y=0^-) = V_0k\left(\mathrm{sen}(kx)\mathbf{u}_x-\cos(kx)\mathbf{u}_y\right)</math></center> | ||
| + | |||
| + | Vemos que la componente tangencial (en la dirección de <math>\mathbf{u}_x</math>) es continua, mientras que la normal (en la dirección de <math>\mathbf{u}_y</math>) cambia de signo. La densidad superficial de carga vale | ||
| + | |||
| + | <center> | ||
| + | <math>\sigma_s = \varepsilon_0\mathbf{u}_y\cdot\left(\mathbf{E}(y=0^+)-\mathbf{E}(y=0^-)\right) = 2\varepsilon_0kV_0\cos(kx)</math></center> | ||
| + | |||
| + | La distribución de carga a lo largo del plano <math>y=0</math> es sinusoidal, con zonas donde la carga es positiva y zonas donde los es negativa. Las líneas de campo reflejan este hecho, descirbiendo arcos que van desde las zonas cargadas positivamente a las de signo opuesto. | ||
| + | |||
| + | <center>[[Imagen:planoseno.png]]</center> | ||
[[Categoría:Problemas de electrostática en el vacío]] | [[Categoría:Problemas de electrostática en el vacío]] | ||
última version al 14:14 26 nov 2008
Contenido |
1 Enunciado
El potencial eléctrico en todos los puntos del espacio viene dado por la ecuación
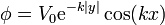
con k y V0 constantes.
- Halle el campo eléctrico en todos los puntos del espacio.
- Calcule la densidad de carga que crea este campo eléctrico.
2 Solución
2.1 Campo eléctrico
Para calcular el campo debemos hallar el gradiente del potencial, cambiado de signo.
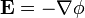
Para esto es conveniente separa el potencial en dos regiones
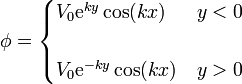
Hallando ahora el gradiente en cada región tenemos,
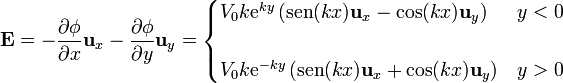
o, agrupando los dos casos
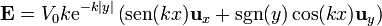
2.2 Densidad de carga
2.2.1 Volumétrica
La densidad de carga de volumen la obtenemos por aplicación de la ley de Gauss en forma diferencial
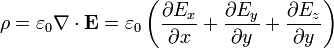
Para hallar esta cantidad volvemos a descomponer en los dos semiespacios. Para y > 0 tenemos
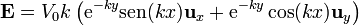
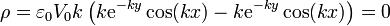
y para y < 0

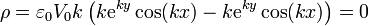
Por tanto, la densidad de carga de volumen es nula en todos los puntos del espacio. Puesto que el campo no es nulo, y además se anula en el infinito, es claro que debe haber alguna densidad de carga adicional. Esta densidad es la superficial, que se encuentra en las superficies donde el campo es discontinuo.
2.2.2 Superficial
La densidad de carga superficial sólo puede estar presente en las superficies de discontinuidad, siendo su valor
![\sigma_s = \varepsilon_0 \mathbf{n}\cdot\left[\mathbf{E}\right]](/wiki/images/math/9/5/a/95a77b9f6c7efed7a82e4e9d96b429dd.png)
En nuestro caso, el único salto en el campo eléctrico se da en y = 0, a cuyos lados el campo vale

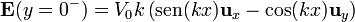
Vemos que la componente tangencial (en la dirección de 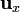 ) es continua, mientras que la normal (en la dirección de
) es continua, mientras que la normal (en la dirección de 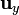 ) cambia de signo. La densidad superficial de carga vale
) cambia de signo. La densidad superficial de carga vale
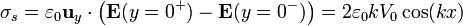
La distribución de carga a lo largo del plano y = 0 es sinusoidal, con zonas donde la carga es positiva y zonas donde los es negativa. Las líneas de campo reflejan este hecho, descirbiendo arcos que van desde las zonas cargadas positivamente a las de signo opuesto.