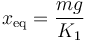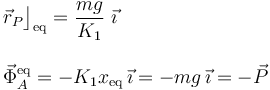Ejercicio de partícula vinculada en equilibrio, Noviembre 2012 (F1 GIA)

De Laplace

Revisión de 19:30 7 ene 2013 (ver código fuente) Gabriel (Discusión | contribuciones) (→Equilibrio del sistema) ← Edición más antigua		última version al 21:11 7 ene 2013 (ver código fuente) Gabriel (Discusión | contribuciones) (→Equilibrio del sistema)
(18 ediciones intermedias no se muestran.)
Línea 22:		Línea 22:
	El resorte de constante recuperadora <math>K_1</math> tienen longitud natural despreciable y sus extremos conectados a ambas partículas. Por tanto, la fuerza que ejerce sobre la partícula <math>A</math> es:		El resorte de constante recuperadora <math>K_1</math> tienen longitud natural despreciable y sus extremos conectados a ambas partículas. Por tanto, la fuerza que ejerce sobre la partícula <math>A</math> es:
-	<center><math>\vec{F}_1(A)=K_1\!\ \overrightarrow{AP}=K_1\!\ \left[\vec{r}_P-\vec{r}_A\right]=K_1 \!\ \left(-x\!\ \vec{\imath}+y\!\ \vec{\jmath}\!\ \right)</math></center>	+	<center><math>\vec{F}_1(A)=K_1\!\ \overrightarrow{AP}=K_1 \left[\vec{r}_P-\vec{r}_A\right]=K_1 \left(x\!\ \vec{\imath}-y\!\ \vec{\jmath}\!\ \right)</math></center>
	El segundo resorte tiene sus extremos conectado al punto fijo <math>O</math> y a la partícula <math>A</math>, y su longitud natural tiene un valor <math>l_0</math>, no nulo. Así, la fuerza que ejerce sobre esta partícula es:		El segundo resorte tiene sus extremos conectado al punto fijo <math>O</math> y a la partícula <math>A</math>, y su longitud natural tiene un valor <math>l_0</math>, no nulo. Así, la fuerza que ejerce sobre esta partícula es:
-	<center><math>\vec{F}_2(A)=K_2\!\ \bigg(|\overrightarrow{OA}|-l_0\bigg)\!\ \frac{\overrightarrow{AO}}{|\overrightarrow{OA}|}=K_2 \!\ \big(y-l_0\big) \!\ \vec{\jmath}</math></center>	+	<center><math>\vec{F}_2(A)=K_2\!\ \bigg(|\overrightarrow{OA}|-l_0\bigg)\!\ \frac{\overrightarrow{AO}}{|\overrightarrow{OA}|}=K_2 \!\ \big(l_0-y\big) \!\ \vec{\jmath}</math></center>
	===Fuerzas aplicadas en la partícula P===		===Fuerzas aplicadas en la partícula P===
Línea 35:		Línea 35:
	Además, hay dos fuerzas activas aplicadas a esta partícula: la fuerza peso, que describe la interacción gravitatoria sobre esta partícula de masa <math>m</math>, y la fuerza de constante recuperadora <math>K_1</math>. Ésta actúa sobre el extremo <math>P</math> de manera que el resorte recupere su longitud natural nula:		Además, hay dos fuerzas activas aplicadas a esta partícula: la fuerza peso, que describe la interacción gravitatoria sobre esta partícula de masa <math>m</math>, y la fuerza de constante recuperadora <math>K_1</math>. Ésta actúa sobre el extremo <math>P</math> de manera que el resorte recupere su longitud natural nula:
-	<center><math>\vec{P}=m\!\ \vec{g}=mg\!\ \vec{\imath}\mathrm{;}\qquad\vec{F}_1(P)=K_1\!\ \overrightarrow{PA}=K_1 \!\ \left(x\!\ \vec{\imath}-y\!\ \vec{\jmath}\!\ \right)=-\vec{F}_1(A)</math></center>	+	<center><math>\vec{P}=m\!\ \vec{g}=mg\!\ \vec{\imath}\mathrm{;}\qquad\vec{F}_1(P)=K_1\!\ \overrightarrow{PA}=K_1 \left(x\!\ \vec{\imath}-y\!\ \vec{\jmath}\!\ \right)=-\vec{F}_1(A)</math></center>
	Es decir, las respectivas fuerzas que ejerce este resorte en sus extremos son opuestas, tal como establece el principio de acción y reacción.		Es decir, las respectivas fuerzas que ejerce este resorte en sus extremos son opuestas, tal como establece el principio de acción y reacción.
	===Equilibrio del sistema===		===Equilibrio del sistema===
-	El sistema estará en equilibrio cuando todas sus partes se hallen en dicho estado. Es decir, cada una de los dos partículas debe estar en equilibrio, para lo cual es condición necesaria que las resultantes de las fuerzas aplicadas sobre cada una de ellas sean nulas.	+	El sistema estará en equilibrio cuando todas sus partes se hallen en dicho estado. Es decir, cada una de los dos partículas debe estar en equilibrio, para lo cual es condición necesaria que las resultantes de las fuerzas aplicadas sobre cada una de ellas sean nulas:
-	<center><math>\vec{r}_A=y_\mathrm{eq}\vec{\jmath}=\overrightatow{OA}_\mathrm{eq}\mathrm{,}\;\;\mathrm{ctes.}\quad\Longrightarrow\quad \vec{F}_1(A_\mathrm{eq})+\vec{F}_2(A_\mathrm{eq})+\vec{\Phi}_A^\mathrm{eq}=\vec{0}</math></center>	+	<center><math>\vec{r}_A\big\rfloor_\mathrm{eq}=y_\mathrm{eq}\!\ \vec{\jmath}=\overrightarrow{OA}_\mathrm{eq}\mathrm{,}\;\;\mathrm{cte.}\quad\Longrightarrow\quad \vec{F}_1(A_\mathrm{eq})+\vec{F}_2(A_\mathrm{eq})+\vec{\Phi}_A^\mathrm{eq}=\vec{0}\quad\longleftrightarrow\quad\left\{\begin{array}{l}\displaystyle K_1x_\mathrm{eq}+\Phi_x^A=0\\ \\
		+	-K_1y_\mathrm{eq}+K_2(l_0-y_\mathrm{eq})=0\\ \\
		+	\Phi_z^A=0\end{array}\right.</math></center>
-	<center><math>\vec{r}_A=y_\mathrm{eq}\vec{\jmath}\mathrm{,}\;\;\vec{r}_P=x_\mathrm{eq}\vec{\imath}\mathrm{,}\;\;\mathrm{ctes.}\quad\Longrightarrow\quad\left\{\begin{array}{l}\displaystyle \vec{F}_1(A_\mathrm{eq})+\vec{F}_2(A_\mathrm{eq})+\vec{\Phi}_A^\mathrm{eq}=\vec{0}\\ \\ \displaystyle \vec{F}_1(P_\mathrm{eq})+\vec{P}+\vec{\Phi}_P^\mathrm{eq}=\vec{0}\end{array}\right.</math></center>	+	&nbsp;
		+
		+	<center><math>\vec{r}_P\big\rfloor_\mathrm{eq}=x_\mathrm{eq}\!\ \vec{\imath}=\overrightarrow{OP}_\mathrm{eq}\mathrm{,}\;\;\mathrm{cte.}\quad\Longrightarrow\quad \vec{F}_1(P_\mathrm{eq})+\vec{P}+\vec{\Phi}_P^\mathrm{eq}=\vec{0}\quad\longleftrightarrow\quad\left\{\begin{array}{l}\displaystyle -K_1x_\mathrm{eq}+mg=0\\ \\
		+	K_1y_\mathrm{eq}+\Phi_y^P=0\\ \\
		+	\Phi_z^P=0\end{array}\right.</math></center>
		+
		+	Este sistema de seis ecuaciones permite determinar tanto las posiciones de equilibrio, como los valores de las fuerzas de reacción vincular que actúan sobre las partículas en dichas posiciones.
		+
		+	De la segunda ecuación se obtiene la posición de equilibrio de la partícula sin masa <math>A</math>; y este resultado, junto con las ecuaciones quinta
		+	y sexta, permite determinar la reacción vincular que el eje vertical ejerce sobre la partícula <math>P</math>:
		+
		+	<center><math>y_\mathrm{eq}=\frac{K_2}{K_1+K_2}\ l_0</math>{{qquad}}{{tose}}{{qquad}}<math style="border:solid blue 2px;padding:10px">\begin{array}{l}\displaystyle \vec{r}_A\big\rfloor_\mathrm{eq}=\frac{K_2}{K_1+K_2}\ l_0\!\ \vec{\jmath}\\ \\ \displaystyle
		+	\vec{\Phi}_P^\mathrm{eq}=-K_1y_\mathrm{eq}\!\ \vec{\jmath}=-\frac{K_1K_2\!\ l_0}{K_1+K_2}\ \vec{\jmath}\end{array}</math></center>
		+
		+	Análogamente, la cuarta ecuación algebraica proporciona la posición de equilibrio de la partícula <math>P</math>; y esta posición, permite determinar la fuerza de reacción vincular ejercida por la barra horizontal sobre la partícula <math>A</math>:
		+
		+	<center><math>x_\mathrm{eq}=\frac{mg}{K_1}</math>{{qquad}}{{tose}}{{qquad}}<math style="border:solid red 2px;padding:10px">\begin{array}{l}\displaystyle \vec{r}_P\big\rfloor_\mathrm{eq}=\frac{mg}{K_1}\ \vec{\imath}\\ \\ \displaystyle
		+	\vec{\Phi}_A^\mathrm{eq}=-K_1x_\mathrm{eq}\!\ \vec{\imath}=-mg\!\ \vec{\imath}=-\vec{P}\end{array}</math></center>

---

última version al 21:11 7 ene 2013

Contenido 1 Enunciado 2 Solución 2.1 Fuerzas aplicadas en la partícula A 2.2 Fuerzas aplicadas en la partícula P 2.3 Equilibrio del sistema

1 Enunciado

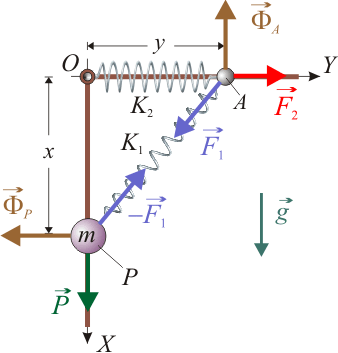
El sistema de la figura está formado por dos barras fijas conectadas en el punto O y dirigidas, una en la dirección de la vertical gravitatoria OX, y otra en una dirección horizontal OY. Una partícula pesada P, de masa m, se halla ensartada en la barra vertical, pudiendo deslizar por ella sin rozamiento. Un segundo punto material A, cuya masa es despreciable, está obligado a moverse siempre en la barra horizontal. Un resorte de longitud natural nula y constante recuperadora K₁ tiene conectados cada uno de sus extremos a dichos puntos móviles. Un segundo resorte de constante K₂ y longitud natural l₀ conecta la partícula sin masa A con el punto fijo O. Considerando que el rozamiento entre la barra horizontal y la partícula A es también despreciable, determine las posiciones que ocupan las partículas y las fuerzas de reacción vincular que actúan sobre ellas cuando ambas se encuentran en equilibrio.

2 Solución

Consideremos que el sistema se haya en una posición arbitraria en que las partículas A y P, ensartadas en sendos ejes horizontal y vertical, ocupan las posiciones dadas por los vectores posición,

Y para que estas posiciones sean de equilibrio, es condición necesaria que sean nulas cada una de las resultantes de las fuerzas aplicadas sobre las partículas.

2.1 Fuerzas aplicadas en la partícula A

En el enunciado se indica que la partícula insertada en la barra horizontal (perpendicular a la dirección de la gravedad), tiene masa nula o despreciable frente a la de la otra partícula. Por tanto, no hemos de considerar la fuerza peso que actúa sobre dicha partícula: sólo la acción de los resortes y la fuerza de reacción vincular que impide cualquier desplazamiento no compatible con el vínculo geométrico descrito.

La partícula sólo puede desplazarse a lo largo de la barra horizontal que hemos identificado con el eje OY. Por tanto, aplicamos el principio de liberación y consideramos la existencia de una fuerza de reacción vincular 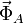que sólo permite dichos desplazamientos:

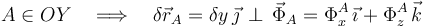
En el enunciado que indica que los rozamientos entre partículas y barras son despreciables; es decir, los vínculos son geométricos y lisos, por lo que la anterior fuerza de reacción vincular caracteriza completamenta el contacto entre la barra horizontal y la partícula A.

El resorte de constante recuperadora K₁ tienen longitud natural despreciable y sus extremos conectados a ambas partículas. Por tanto, la fuerza que ejerce sobre la partícula A es:

El segundo resorte tiene sus extremos conectado al punto fijo O y a la partícula A, y su longitud natural tiene un valor l₀, no nulo. Así, la fuerza que ejerce sobre esta partícula es:

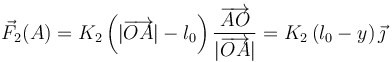
2.2 Fuerzas aplicadas en la partícula P

Se trata también de una partícula sometida a un vínculo geométrico, bilateral y liso, consistente en permanecer siempre sobre el eje vertical. Para aplicar el principio de liberación en este partícula consideramos una fuerza de reacción vicnular que impide todo desplazamiento no compatible la restricción descrita:

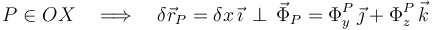
Además, hay dos fuerzas activas aplicadas a esta partícula: la fuerza peso, que describe la interacción gravitatoria sobre esta partícula de masa m, y la fuerza de constante recuperadora K₁. Ésta actúa sobre el extremo P de manera que el resorte recupere su longitud natural nula:

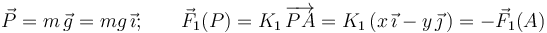
Es decir, las respectivas fuerzas que ejerce este resorte en sus extremos son opuestas, tal como establece el principio de acción y reacción.

2.3 Equilibrio del sistema

El sistema estará en equilibrio cuando todas sus partes se hallen en dicho estado. Es decir, cada una de los dos partículas debe estar en equilibrio, para lo cual es condición necesaria que las resultantes de las fuerzas aplicadas sobre cada una de ellas sean nulas:

 

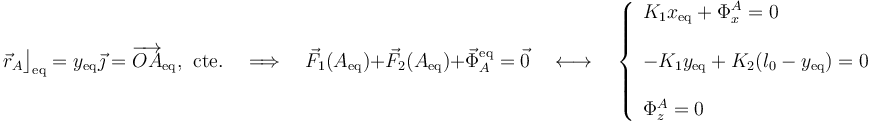
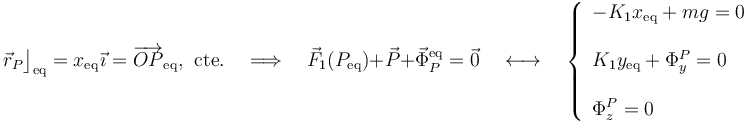
Este sistema de seis ecuaciones permite determinar tanto las posiciones de equilibrio, como los valores de las fuerzas de reacción vincular que actúan sobre las partículas en dichas posiciones.

De la segunda ecuación se obtiene la posición de equilibrio de la partícula sin masa A; y este resultado, junto con las ecuaciones quinta y sexta, permite determinar la reacción vincular que el eje vertical ejerce sobre la partícula P:

              

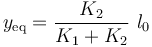
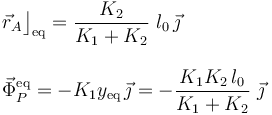
Análogamente, la cuarta ecuación algebraica proporciona la posición de equilibrio de la partícula P; y esta posición, permite determinar la fuerza de reacción vincular ejercida por la barra horizontal sobre la partícula A: