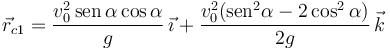2.6. Tiro parabólico
De Laplace
(→Celeridad y vector tangente) |
m (3.6. Tiro parabólico trasladada a 2.6. Tiro parabólico) |
||
| (22 ediciones intermedias no se muestran.) | |||
| Línea 10: | Línea 10: | ||
# Determine el vector de posición, la velocidad y la aceleración en cada instante. | # Determine el vector de posición, la velocidad y la aceleración en cada instante. | ||
| - | # Calcule la celeridad y el vector tangente en el instante en el cual el proyectil se encuentra a | + | # Calcule la celeridad y el vector tangente en el instante en el cual el proyectil se encuentra a máxima altura. |
# Halle la aceleración tangencial y la aceleración normal, así como el vector unitario normal, en el mismo instante del apartado anterior. | # Halle la aceleración tangencial y la aceleración normal, así como el vector unitario normal, en el mismo instante del apartado anterior. | ||
# Calcule el radio de curvatura y el centro de curvatura en el punto más alto de la trayectoria. | # Calcule el radio de curvatura y el centro de curvatura en el punto más alto de la trayectoria. | ||
| Línea 23: | Línea 23: | ||
<center><math>\vec{r}_0 =\vec{0}</math></center> | <center><math>\vec{r}_0 =\vec{0}</math></center> | ||
| - | mientras que la velocidad inicial posee módulo <math>v_0</math> y forma un ángulo <math>\alpha</math> con la horizontal | + | mientras que la velocidad inicial posee módulo <math>v_0\,</math> y forma un ángulo <math>\alpha</math> con la horizontal |
<center><math>\vec{v}_0 = v_0\cos(\alpha)\vec{\imath}+v_0\,\mathrm{sen}(\alpha)\vec{k}</math></center> | <center><math>\vec{v}_0 = v_0\cos(\alpha)\vec{\imath}+v_0\,\mathrm{sen}(\alpha)\vec{k}</math></center> | ||
| Línea 29: | Línea 29: | ||
lo que nos da el vector de posición en cada instante | lo que nos da el vector de posición en cada instante | ||
| - | <center><math>\vec{r}=(v_0\cos\alpha)t\vec{\imath}+\left((v_0\,\mathrm{sen}\,\alpha)t-\frac{1}{2}gt^2\right)\vec{k}</math></center> | + | <center><math>\vec{r}=(v_0\cos\alpha)t\,\vec{\imath}+\left((v_0\,\mathrm{sen}\,\alpha)t-\frac{1}{2}gt^2\right)\vec{k}</math></center> |
Derivando el vector de posición respecto al tiempo obtenemos la velocidad intantánea | Derivando el vector de posición respecto al tiempo obtenemos la velocidad intantánea | ||
| Línea 55: | Línea 55: | ||
</center> | </center> | ||
| - | ==Celeridad y vector tangente== | + | ==Celeridad y vector tangente en el punto de máxima altura== |
| - | El instante <math>t_1\,</math> en el que debemos calcular las diferentes magnitudes es | + | El instante <math>t_1\,</math> en el que debemos calcular las diferentes magnitudes es aquel en el cual el proyectil alcanza su máxima altura. Ésta se alcanza cuando <math>z</math> tiene un máximo, esto es, cuando la componente <math>z</math> de la velocidad es nula |
| - | + | ||
| - | + | ||
<center><math>0 = \frac{\mathrm{d}z}{\mathrm{d}t}=v_z = v_0\,\mathrm{sen}\,\alpha-gt_1</math>{{tose}} <math>t_1 = \frac{v_0\,\mathrm{sen}\,\alpha}{g}</math></center> | <center><math>0 = \frac{\mathrm{d}z}{\mathrm{d}t}=v_z = v_0\,\mathrm{sen}\,\alpha-gt_1</math>{{tose}} <math>t_1 = \frac{v_0\,\mathrm{sen}\,\alpha}{g}</math></center> | ||
| - | La posición, velocidad y aceleración | + | La posición, velocidad y aceleración en este instante las hallamos sustituyendo en las ecuaciones anteriores |
| - | + | <center><math>\vec{r}_1=\frac{v_0^2\,\mathrm{sen}\,\alpha\cos\alpha}{g}\vec{\imath}+\frac{v_0^2\,\mathrm{sen}^2\alpha}{2g}\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{v}_1=v_0\cos\alpha\,\vec{\imath}</math>{{qquad}}{{qquad}}<math>\vec{a}_1=-g\,\vec{k}</math></center> | |
| - | <center><math>\vec{r}_1=\frac{v_0^2\,\mathrm{sen}\,\alpha\cos\alpha}{g}\vec{\imath}+\frac{v_0^2\,\mathrm{sen}^2\alpha}{2g}\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{v}_1=v_0\cos\alpha\vec{\imath}</math>{{qquad}}{{qquad}}<math>\vec{a}_1=-g\vec{k}</math></center> | + | |
===Celeridad=== | ===Celeridad=== | ||
| - | + | La celeridad es el módulo de la velocidad. Para el instante estudiado vale | |
| - | |||
<center><math>v_1 = v_0\cos\alpha\,</math></center> | <center><math>v_1 = v_0\cos\alpha\,</math></center> | ||
| Línea 76: | Línea 72: | ||
Obtenemos el vector tangente en el instante estudiado dividiendo la velocidad por su módulo | Obtenemos el vector tangente en el instante estudiado dividiendo la velocidad por su módulo | ||
| - | + | <center><math>\vec{T}_1 = \frac{\vec{v}_1}{v_1}=\vec{\imath}</math></center> | |
| - | <center><math>\vec{T}_1 = \frac{\vec{v} | + | |
| - | ==Componentes intrínsecas de la aceleración== | + | ==Componentes intrínsecas de la aceleración en el punto de máxima altura== |
===Aceleración tangencial=== | ===Aceleración tangencial=== | ||
Obtenemos la componente tangencial de la aceleración proyectando sobre el vector tangente | Obtenemos la componente tangencial de la aceleración proyectando sobre el vector tangente | ||
| Línea 85: | Línea 80: | ||
<center><math>a_t = \vec{a}\cdot\vec{T}=\frac{\vec{a}\cdot\vec{v}}{v}</math></center> | <center><math>a_t = \vec{a}\cdot\vec{T}=\frac{\vec{a}\cdot\vec{v}}{v}</math></center> | ||
| - | Para | + | Para el instante señalado es |
| - | + | <center><math>a_{t1}=0\,</math></center> | |
| - | <center><math>a_{t1}= | + | |
| - | + | Esta nulidad de la aceleración tangencial sólo se produce en el punto de la trayectoria que estamos analizando (punto de máxima altura), y nos informa de que la celeridad del proyectil alcanza un mínimo en el vértice de la parábola. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
En forma vectorial la aceleración tangencial es | En forma vectorial la aceleración tangencial es | ||
| Línea 104: | Línea 92: | ||
que nos da | que nos da | ||
| - | + | <center><math>\vec{a}_{t1}=\vec{0}\,</math></center> | |
| - | <center><math>\vec{a}_{t1 | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
===Aceleración normal=== | ===Aceleración normal=== | ||
| Línea 117: | Línea 98: | ||
[[Archivo:parabolico-atn.gif|right]] | [[Archivo:parabolico-atn.gif|right]] | ||
| - | Una vez que tenemos la aceleración tangencial | + | Una vez que tenemos la aceleración tangencial, calculamos la aceleración normal restando |
<center><math>\vec{a}_n = \vec{a}-\vec{a}_t</math></center> | <center><math>\vec{a}_n = \vec{a}-\vec{a}_t</math></center> | ||
| - | Lo que nos da | + | Lo que nos da: |
| - | + | <center><math>\vec{a}_{n1}=-g\,\vec{k}</math></center> | |
| - | <center><math>\vec{a}_{n1}=- | + | |
| - | + | En módulo, esta aceleración normal vale | |
| - | + | ||
| - | + | <center><math>a_{n1}=g\,</math></center> | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | <center><math>a_{n1}=g | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
===Vector normal=== | ===Vector normal=== | ||
| Línea 153: | Línea 120: | ||
y nos da | y nos da | ||
| - | + | <center><math>\vec{N}_{1}=-\vec{k}</math></center> | |
| - | <center><math>\vec{N}_{1}= | + | |
| - | + | Vemos que el vector normal apunta hacia el interior de la curva (entendiendo por interior el lado hacia el que se curva). Es inmediato comprobar que este vector es ortogonal al vector tangente. | |
| - | + | ||
| - | + | Podemos hallar el vector binormal multiplicando vectorialmente el vector tangente por el normal | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | Podemos hallar el vector binormal | + | |
<center><math>\vec{B}=\vec{T}\times\vec{N}</math></center> | <center><math>\vec{B}=\vec{T}\times\vec{N}</math></center> | ||
| - | que | + | que da |
| - | <center><math>\vec{B}_1 | + | <center><math>\vec{B}_1=\vec{\jmath}</math></center> |
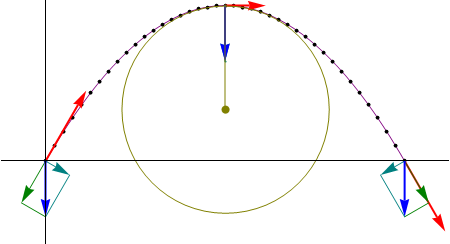
| - | + | El vector binormal calculado en cualquier otro instante del movimiento sería el mismo, ya que estamos ante una trayectoria plana (vector binormal constante). | |
<center>[[Archivo:tiroparabolico.png]]</center> | <center>[[Archivo:tiroparabolico.png]]</center> | ||
| - | ==Radio y centro de curvatura== | + | ==Radio y centro de curvatura en el punto de máxima altura== |
===Radio de curvatura=== | ===Radio de curvatura=== | ||
Una vez que tenemos la aceleración normal y la celeridad hallamos el radio de curvatura como | Una vez que tenemos la aceleración normal y la celeridad hallamos el radio de curvatura como | ||
| Línea 184: | Línea 144: | ||
Sustituyendo tenemos, para el punto de máxima altura | Sustituyendo tenemos, para el punto de máxima altura | ||
| - | <center><math> | + | <center><math>R_1=\frac{v_0^2\cos^2\alpha}{g}</math></center> |
El centro de curvatura lo obtenemos a partir de la posición de la partícula, el radio de curvatura y del vector normal | El centro de curvatura lo obtenemos a partir de la posición de la partícula, el radio de curvatura y del vector normal | ||
| Línea 192: | Línea 152: | ||
lo que nos da, para este punto | lo que nos da, para este punto | ||
| - | <center><math>\vec{r}_{ | + | <center><math>\vec{r}_{c1}=\frac{v_0^2\,\mathrm{sen}\,\alpha\cos\alpha}{g}\,\vec{\imath}+\frac{v_0^2(\mathrm{sen}^2\alpha-2\cos^2\alpha)}{2g}\,\vec{k}</math></center> |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
[[Categoría:Problemas de cinemática del punto material (G.I.T.I.)]] | [[Categoría:Problemas de cinemática del punto material (G.I.T.I.)]] | ||
[[Categoría:Cinemática del punto material (G.I.T.I.)]] | [[Categoría:Cinemática del punto material (G.I.T.I.)]] | ||
última version al 15:21 23 sep 2013
Contenido |
1 Enunciado
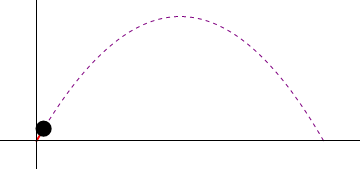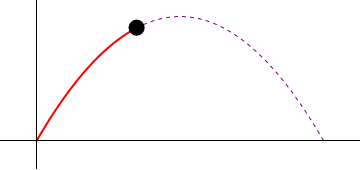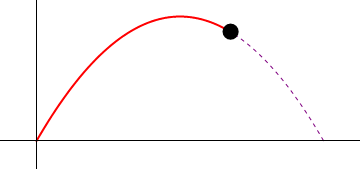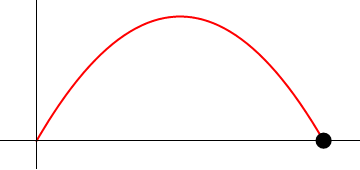
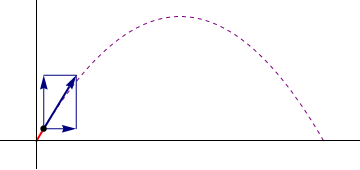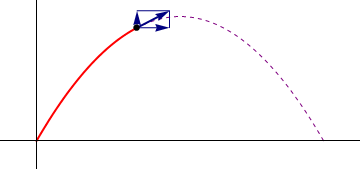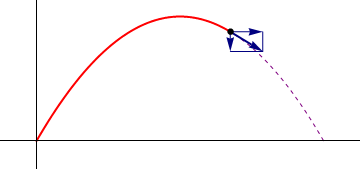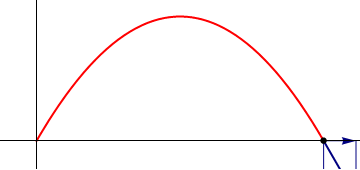
Supóngase el movimiento de un proyectil que se caracteriza por poseer una aceleración constante

una posición inicial nula (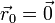 ) y una velocidad inicial que forma un ángulo α con la horizontal y tiene rapidez inicial v0.
) y una velocidad inicial que forma un ángulo α con la horizontal y tiene rapidez inicial v0.
- Determine el vector de posición, la velocidad y la aceleración en cada instante.
- Calcule la celeridad y el vector tangente en el instante en el cual el proyectil se encuentra a máxima altura.
- Halle la aceleración tangencial y la aceleración normal, así como el vector unitario normal, en el mismo instante del apartado anterior.
- Calcule el radio de curvatura y el centro de curvatura en el punto más alto de la trayectoria.
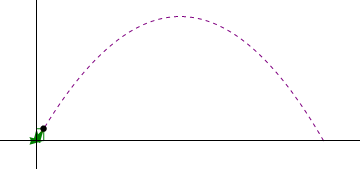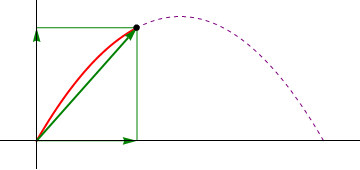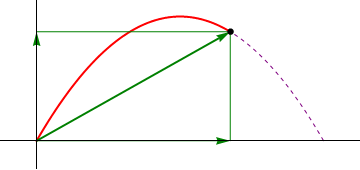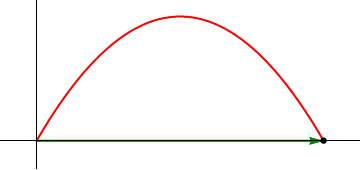
2 Posición, velocidad y aceleración
Al ser la aceleración constante, la integración es inmediata:
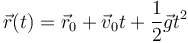
La posición inicial, según nos indica el enunciado, es nula
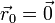
mientras que la velocidad inicial posee módulo 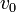 y forma un ángulo α con la horizontal
y forma un ángulo α con la horizontal
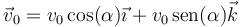
lo que nos da el vector de posición en cada instante
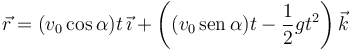
Derivando el vector de posición respecto al tiempo obtenemos la velocidad intantánea

La velocidad de avance horizontal permanece constante, mientras que la vertical varía linealmente con el tiempo. Comienza siendo positiva, se anula en el punto más alto, y a partir de ahí es negativa.
Para la aceleración, derivamos la velocidad instantánea respecto al tiempo y comprobamos que, tal como indica el enunciado, es constante

| 
| 
|
| Posición | Velocidad | Aceleración |
|---|
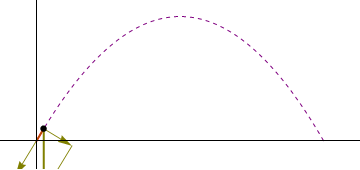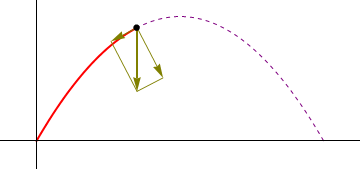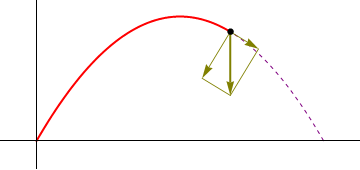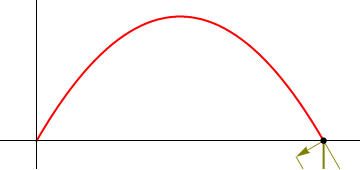
3 Celeridad y vector tangente en el punto de máxima altura
El instante 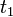 en el que debemos calcular las diferentes magnitudes es aquel en el cual el proyectil alcanza su máxima altura. Ésta se alcanza cuando z tiene un máximo, esto es, cuando la componente z de la velocidad es nula
en el que debemos calcular las diferentes magnitudes es aquel en el cual el proyectil alcanza su máxima altura. Ésta se alcanza cuando z tiene un máximo, esto es, cuando la componente z de la velocidad es nula
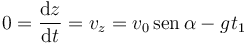

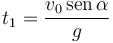
La posición, velocidad y aceleración en este instante las hallamos sustituyendo en las ecuaciones anteriores
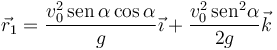
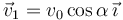
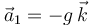
3.1 Celeridad
La celeridad es el módulo de la velocidad. Para el instante estudiado vale
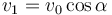
3.2 Vector tangente
Obtenemos el vector tangente en el instante estudiado dividiendo la velocidad por su módulo
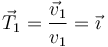
4 Componentes intrínsecas de la aceleración en el punto de máxima altura
4.1 Aceleración tangencial
Obtenemos la componente tangencial de la aceleración proyectando sobre el vector tangente
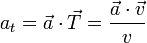
Para el instante señalado es
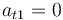
Esta nulidad de la aceleración tangencial sólo se produce en el punto de la trayectoria que estamos analizando (punto de máxima altura), y nos informa de que la celeridad del proyectil alcanza un mínimo en el vértice de la parábola.
En forma vectorial la aceleración tangencial es
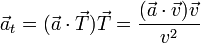
que nos da
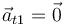
4.2 Aceleración normal
Una vez que tenemos la aceleración tangencial, calculamos la aceleración normal restando
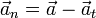
Lo que nos da:
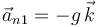
En módulo, esta aceleración normal vale
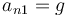
4.3 Vector normal
El vector unitario normal lo hallamos dividiendo la aceleración normal por su módulo
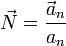
y nos da
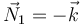
Vemos que el vector normal apunta hacia el interior de la curva (entendiendo por interior el lado hacia el que se curva). Es inmediato comprobar que este vector es ortogonal al vector tangente.
Podemos hallar el vector binormal multiplicando vectorialmente el vector tangente por el normal
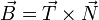
que da
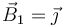
El vector binormal calculado en cualquier otro instante del movimiento sería el mismo, ya que estamos ante una trayectoria plana (vector binormal constante).
5 Radio y centro de curvatura en el punto de máxima altura
5.1 Radio de curvatura
Una vez que tenemos la aceleración normal y la celeridad hallamos el radio de curvatura como
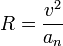
Sustituyendo tenemos, para el punto de máxima altura
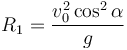
El centro de curvatura lo obtenemos a partir de la posición de la partícula, el radio de curvatura y del vector normal
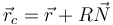
lo que nos da, para este punto