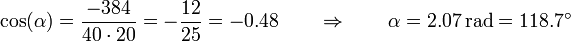Calcular el ángulo entre dos vectores
De Laplace
(Diferencias entre revisiones)
(→Solución) |
|||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 21: | Línea 21: | ||
<center><math>\cos(\alpha)=\frac{-384}{40\cdot20}=-\frac{12}{25}=-0.48\qquad\Rightarrow\qquad \alpha = 2.07\,\mathrm{rad}=118.7^\circ</math></center> | <center><math>\cos(\alpha)=\frac{-384}{40\cdot20}=-\frac{12}{25}=-0.48\qquad\Rightarrow\qquad \alpha = 2.07\,\mathrm{rad}=118.7^\circ</math></center> | ||
| - | [[Categoría:Problemas de | + | [[Categoría:Problemas de herramientas matemáticas (GIE)]] |
última version al 11:51 19 sep 2012
1 Enunciado
Halle el ángulo que forman los vectores
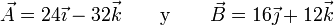
2 Solución
Obtenemos el ángulo a partir del producto escalar de los dos vectores
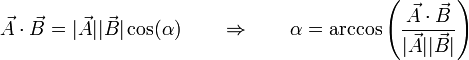
Tenemos que
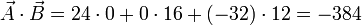
y que
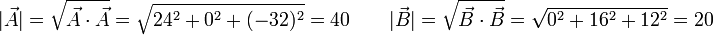
lo que nos da