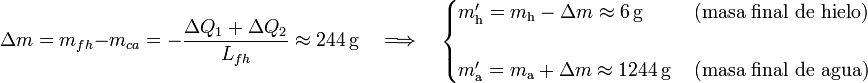Enfriado de agua con hielo GIA
De Laplace
(→Hipótesis C) |
(→Hipótesis C) |
||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 86: | Línea 86: | ||
<center><math>\Delta Q_\mathrm{h}=\Delta Q_2+m_{fh}L_{fh}=-\Delta Q_1+m_{ca}L_{fh}=-\Delta Q_\mathrm{a}\quad\Longrightarrow\quad (m_{fh}-m_{ca})L_{fh}=-\Delta Q_1-\Delta Q_2\approx 81.5\,\mathrm{kJ}\,</math></center> | <center><math>\Delta Q_\mathrm{h}=\Delta Q_2+m_{fh}L_{fh}=-\Delta Q_1+m_{ca}L_{fh}=-\Delta Q_\mathrm{a}\quad\Longrightarrow\quad (m_{fh}-m_{ca})L_{fh}=-\Delta Q_1-\Delta Q_2\approx 81.5\,\mathrm{kJ}\,</math></center> | ||
| + | |||
| + | Es decir, la cantidad de calor cedido por el agua al enfriarse hasta la temperatura del punto de congelación es mayor que el necesario para calentar el hielo hasta dicho punto. En consecuencia, la cantidad <math>m_{fh}</math> de hielo que se funde va a ser mayor que la de agua, <math>m_{ca}</math> que pudiera llegar a congelarse. La diferencia entre estas cantidades será el valor neto de masa de hielo fundida y, por consiguiente, el aumento de masa de agua líquida: | ||
| + | |||
| + | <center><math>\Delta m=m_{fh}-m_{ca}=-\frac{\Delta Q_1+\Delta Q_2}{L_{fh}}\approx 244\,\mathrm{g}\quad \Longrightarrow\quad\begin{cases}m^\prime_\mathrm{h}=m_\mathrm{h}-\Delta m \approx 6\,\mathrm{g}\,&\mbox{(masa final de hielo)}\\ \\ | ||
| + | m^\prime_\mathrm{a}=m_\mathrm{a}+\Delta m \approx 1244\,\mathrm{g}\,&\mbox{(masa final de agua)}\end{cases}</math></center> | ||
| + | |||
| + | |||
| + | <center>[[Archivo:bol_T2_04_3.gif]]</center> | ||
última version al 13:15 13 jun 2012
Contenido |
1 Enunciado
Para enfriar un litro de agua que está a 20°C se le añaden 250 gramos de hielo a -4°C. Determinar el estado final de la mezcla supuestas despreciables las pérdidas de calor.
Datos: calor específico del agua, 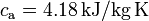 ; calor específico del hielo,
; calor específico del hielo, 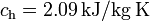 ; calor latente de fusión del hielo,
; calor latente de fusión del hielo, 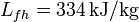 .
.
2 Solución
En primer lugar, consideraremos que la mezcla inicial de hielo y agua se encuentra en un recipiente de paredes fijas, a una presión aproximada de una atmósfera y que, según se indica en el enunciado, las cantidad de calor que intercambia aquél con la mezcla son despreciables. En consecuencia, las únicas transferencias de energía a tener en cuenta, serán las que existan entre la masas 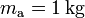 de agua, y
de agua, y 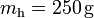 de hielo. Por otra parte, como la primera sustancia es un líquido incompresible, y el hielo es un sólido, admitiremos que la única forma posible de transferencia de energía será en forma de calor, debido a las diferentes temperaturas que inicialmente tienen los componentes de la mezcla. Obsérvese que, como éstos son la misma sustancia pero en diferente fase, las cantidades de calor transferidas en el proceso que termina en el equilibrio térmico, van a producir tanto cambios de temperatura, como cambios de fase, que determinarán el estado final de la mezcla que, a su vez estará condicionado por la temperatura final de equilibrio.
de hielo. Por otra parte, como la primera sustancia es un líquido incompresible, y el hielo es un sólido, admitiremos que la única forma posible de transferencia de energía será en forma de calor, debido a las diferentes temperaturas que inicialmente tienen los componentes de la mezcla. Obsérvese que, como éstos son la misma sustancia pero en diferente fase, las cantidades de calor transferidas en el proceso que termina en el equilibrio térmico, van a producir tanto cambios de temperatura, como cambios de fase, que determinarán el estado final de la mezcla que, a su vez estará condicionado por la temperatura final de equilibrio.
A priori, no podemos asegurar cuál va a ser dicho estado final, y no tenenos más remedio que establecer ciertas hipótesis de trabajo y comprobar si el resultado que se obtiene, es compatible con aquéllas.
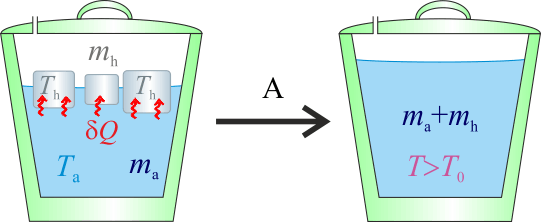
2.1 Hipótesis A
Dado que la cantidad de agua es cuatro veces la hielo y que la diferencia de temperatura de aquélla (Ta) con respecto a la del punto de congelación (T0), es cinco veces mayor que la de éste respecto de la del hielo (Th), resulta una hipótesis plausible que la temperatura de equilibrio, T, esté por encima de la del punto de congelación.
Nótese que esta hipótesis, implica que toda la masa de hielo debe haberse fundido, mientras que la de agua sólo habrá reducido su temperatura. Es decir, el resultado final de la mezcla tras el proceso serían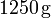 de agua a una temperatura T tal que
de agua a una temperatura T tal que
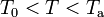
El calor transferido en el proceso a la masa ma de agua líquida sería:
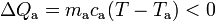
Es decir, es un calor cedido que dependerá de la reducción de temperatura desde el valor inicial Ta, equivalente a 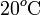 en la escala Celsius, hasta el valor de la temperatura final. En este mismo proceso, el hielo ha de pasar desde una temperatura inicial Th a la que corresponden
en la escala Celsius, hasta el valor de la temperatura final. En este mismo proceso, el hielo ha de pasar desde una temperatura inicial Th a la que corresponden 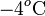 en la escala Celsius, hasta la temperatura final de la mezcla T, pasando previamente por la temperatura T0 correspondiente al punto de congelación del agua (a
en la escala Celsius, hasta la temperatura final de la mezcla T, pasando previamente por la temperatura T0 correspondiente al punto de congelación del agua (a 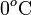 ), en la cuál toda la masa de hielo se funde. Por tanto, el calor transferido al hielo puede descomponerse en tres términos:
), en la cuál toda la masa de hielo se funde. Por tanto, el calor transferido al hielo puede descomponerse en tres términos:
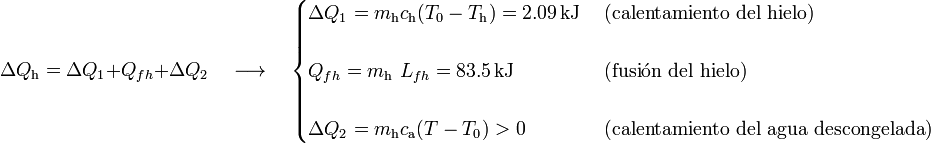
Esta cantidad de calor absorbido debe ser opuesta al cedido por el agua, de manera que,
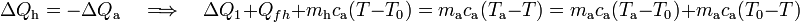
donde en el segundo término hemos restado y sumando el producto de la capacidad calorífica de la masa de agua por la temperatura del punto de congelación, para operar siempre con incrementos de temperatura que, como sabemos, son idénticos en las escalas centrígrada y absoluta. Reordenado estos términos, se obtiene:
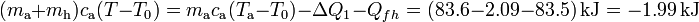
A partir de este resultado parcial, se obtiene que la diferencia entre la temperatura final final de la mezcla, T, y la T0 del punto de congelación sería:
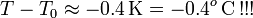
Obsérvese que esta diferencia de temperatura negativa implicaría una temperatura final de unos 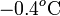 contradiciendo, por tanto, la hipótesis de que T es mayor que la temperatura correspondiente al punto de congelación del agua. En consecuencia, las transferencias de calor que hemos calculado no serán correctas y hemos de rehacer los cálculos para el caso de que la temperatura final esté por debajo del punto de congelación.
contradiciendo, por tanto, la hipótesis de que T es mayor que la temperatura correspondiente al punto de congelación del agua. En consecuencia, las transferencias de calor que hemos calculado no serán correctas y hemos de rehacer los cálculos para el caso de que la temperatura final esté por debajo del punto de congelación.
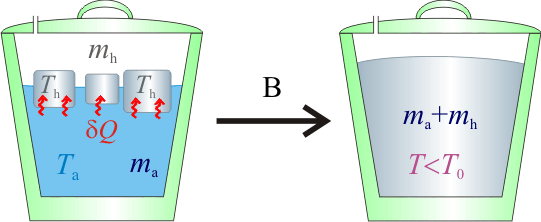
2.2 Hipótesis B
Si la temperatura final queda por debajo del punto de congelación, esto implicaría que toda la masa de agua líquida debería acabar congelada. Esto resulta bastante extraño. Sin embargo, calculemos cuáles serían los calores transferidos en este caso y obtengamos el hipotético valor de temperatura bajo cero resultante que, de todas formas, sería mayor que la Th inicial del hielo:
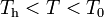
En consecuencia, la masa inicial de hielo sólo habrá sufrido un cierto calentamiento, pero sin llegar a cambiar de fase. En dicho proceso habrá absorbido una cantidad indeterminada de calor,
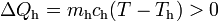
Este calor será cedido por la masa ma de agua al enfriarse desde la temperatura Ta (correspondiente a 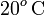 en la escala Celsius), hasta la temperatura final T por debajo de
en la escala Celsius), hasta la temperatura final T por debajo de 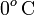 , lo cual exigiría la congelación de la masa de agua inicialmente líquida. De manera análoga al apartado anterior, la cantidad de calor transferida desde el agua puede descomponerse en tres términos:
, lo cual exigiría la congelación de la masa de agua inicialmente líquida. De manera análoga al apartado anterior, la cantidad de calor transferida desde el agua puede descomponerse en tres términos:
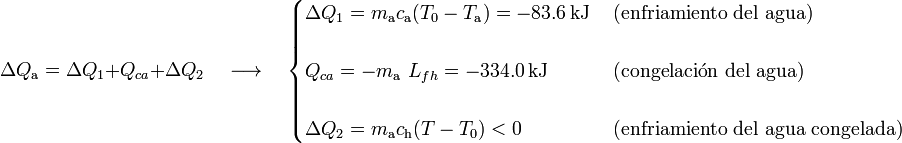
Operando de forma similar a como se hizo en la hipótesis anterior, se tendrá...
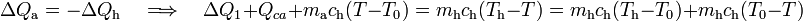
Y agrupando en un mismo miembro los términos que dependen de la temperatura final, se obtiene:
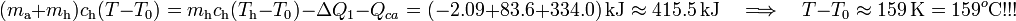
Es decir, llegamos de nuevo a un resultado incompatible con la hipótesis de trabajo: partiendo de que la temperatura final va a estar por debajo del punto de congelación y, por tanto, todo la masa de agua se ha acabado congelando, llegamos al resultado de que el valor de la temperatura final ¡¡es de unos 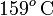 !!
!!
Luego si ambas hipótesis, T > T0 y T < T0, llevan a sendos resultados inconsistentes, la única opción posible es que la temperatura final de equilibrio sea la T0 correspondiente al punto de congelación.
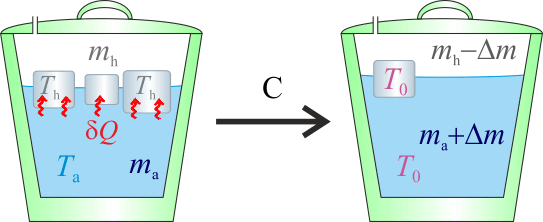
2.3 Hipótesis C
Y si la temperatura resultante es T0, el estado final será, en general, una mezcla de hielo y agua a 0oC, pudiendo ocurrir tanto que una cierta cantidad de hielo mhf se funda, como que otra cantidad mca de agua acabe congelándose. De esta forma, la masa de agua cedería calor para disminuir su temperatura desde Ta hasta T0, y para que se congelase la cantidad indeterminada mca:
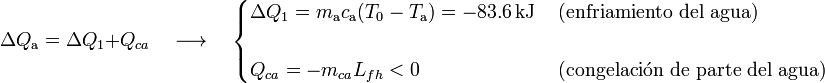
Por su parte, la masa de hielo absorbería calor para elevar su temperatura hasta los 0oC y también para la posible fusión de una cierta cantidad mfh de dicha masa:
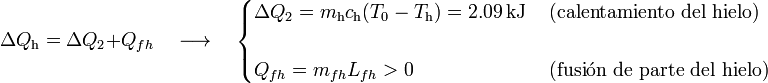
Aplicando una vez más que las anteriores cantidades de calor deben ser opuestas, se obtiene:
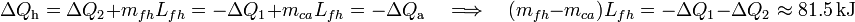
Es decir, la cantidad de calor cedido por el agua al enfriarse hasta la temperatura del punto de congelación es mayor que el necesario para calentar el hielo hasta dicho punto. En consecuencia, la cantidad mfh de hielo que se funde va a ser mayor que la de agua, mca que pudiera llegar a congelarse. La diferencia entre estas cantidades será el valor neto de masa de hielo fundida y, por consiguiente, el aumento de masa de agua líquida: