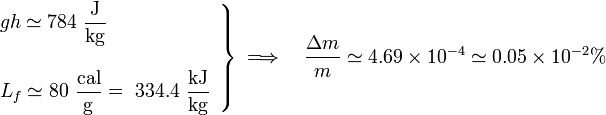Transformación de energía potencial gravitatoria en calor
De Laplace
(→Solución) |
(→Solución) |
||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 3: | Línea 3: | ||
==Solución== | ==Solución== | ||
| - | Aquí tenemos una situación en que la energía mecánica se transforma en calor. Cuando el bloque está a una altura <math>h</math> sobre el | + | Aquí tenemos una situación en que la energía mecánica se transforma en calor. Cuando el bloque está a una altura <math>h=80\,m</math> sobre el |
suelo, y en reposo, su energía mecánica es igual a la energía potencial gravitatoria. Si se toma como origen de potencial coincidiendo con el suelo, se tendrá que, | suelo, y en reposo, su energía mecánica es igual a la energía potencial gravitatoria. Si se toma como origen de potencial coincidiendo con el suelo, se tendrá que, | ||
| Línea 17: | Línea 17: | ||
Como éste se encuentra a una temperatura de <math>0^o\mathrm{C}</math>, este calor absorbido se invierte en primer lugar, en derretir | Como éste se encuentra a una temperatura de <math>0^o\mathrm{C}</math>, este calor absorbido se invierte en primer lugar, en derretir | ||
| - | una parte <math>\Delta m</math> de la masa total de hielo. Si <math>L_f</math> es el calor latente de fusión del hielo a una atmósfera de presión, se tendrá | + | una parte <math>\Delta m</math> de la masa total de hielo. Si <math>L_f</math> es el calor latente de fusión del hielo a una atmósfera de presión, se tendrá que, |
<center> | <center> | ||
<math> | <math> | ||
| - | \Delta m=\frac{\Delta Q}{L_f}=\frac{\lambda mgh}{L_f} | + | \Delta m=\frac{\Delta Q}{L_f}=\frac{\lambda mgh}{L_f}\quad\Longrightarrow\quad\frac{\Delta m}{m}=\frac{\lambda gh}{L_f} |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | \frac{ | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
</math> | </math> | ||
</center> | </center> | ||
| + | es la fracción de masa derretida. En función de los datos del problema, se obtiene: | ||
| + | |||
| + | <center><math>\left.\begin{array}{l}\displaystyle gh\simeq 784\ \frac{\mathrm{J}}{\mathrm{kg}}\\ \\ \displaystyle L_f\simeq 80\ \frac{\mathrm{cal}}{\mathrm{g}}=\ 334.4\ \frac{\mathrm{kJ}}{\mathrm{kg}}\end{array}\right\}\;\Longrightarrow\quad\frac{\Delta m}{m}\simeq 4.69\times 10^{-4}\simeq 0.05\times 10^{-2}\%</math></center> | ||
| + | |||
[[Categoría:Problemas del primer principio de la termodinámica]][[Categoría:Problemas de Primer Principio F2 GIA]] | [[Categoría:Problemas del primer principio de la termodinámica]][[Categoría:Problemas de Primer Principio F2 GIA]] | ||
última version al 11:55 6 jun 2012
1 Enunciado
Un bloque de hielo a 0°C se deja caer libremente desde una altura de 80 m. En el momento del choque, un 20% de la energía del bloque se transforma en calor absorbible por su masa. ¿Que parte del hielo se funde a causa de esta absorción?
2 Solución
Aquí tenemos una situación en que la energía mecánica se transforma en calor. Cuando el bloque está a una altura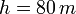 
sobre el
suelo, y en reposo, su energía mecánica es igual a la energía potencial gravitatoria. Si se toma como origen de potencial coincidiendo con el suelo, se tendrá que,
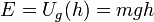
donde m es la masa de hielo, y g la aceleración de la gravedad en las proximidades de la superficie terrestre. En el proceso de caída la energía potencial se va transformado en energía cinética, pero manteniéndose constante la energía mecánica total pues, si se desprecia el rozamiento del hielo con el aire, la única fuerza que actúa es el peso que, como se sabe, es conservativa:
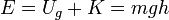
En el instante de impacto inminente, toda la energía potencial inicial se habrá transformado en cinética y, al chocar con el suelo, una fracción λ = 0.2 (es decir, el 20%) de esa energía mecánica se transforma en calor absorbible por el hielo:
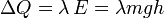
Como éste se encuentra a una temperatura de 0oC, este calor absorbido se invierte en primer lugar, en derretir una parte Δm de la masa total de hielo. Si Lf es el calor latente de fusión del hielo a una atmósfera de presión, se tendrá que,
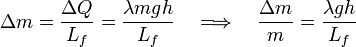
es la fracción de masa derretida. En función de los datos del problema, se obtiene:
