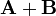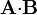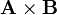Entrar Página Discusión Historial Go to the site toolbox

Operaciones con vectores en diferentes sistemas

De Laplace

(Diferencias entre revisiones)
(Nueva página: ==Enunciado== Dados los vectores <center><math>\mathbf{A} = \mathbf{u}_{\rho}-\mathbf{u}_{z}</math>{{qquad}} <math>\mathbf{B} = 5\mathbf{u}_{r}+12\mathbf{u}_{\theta}</math></center> ...)
(→Producto escalar)
 
(7 ediciones intermedias no se muestran.)
Línea 12: Línea 12:
==Solución==
==Solución==
 +
La única complicación de este problema consiste en expresar ambos vectores en la misma base, ya que, aunque se encuentran evaluados en el mismo punto, uno se encuentra en la base de esféricas y el otro en la de cilíndricas.
 +
 +
Para operar conviene reducirlos a una base común. Ésta no tiene por qué ser la base cartesiana, sino que nos vale la cilíndrica o la esférica (o, cualquier otra, en realidad).
 +
 +
Si empleamos la base de cilíndricas, tenemos que
 +
 +
<center><math>\mathbf{u}_{r}=\mathrm{sen}\,\theta \mathbf{u}_{\rho}+\cos\theta\mathbf{u}_{z}</math>{{qquad}}
 +
<math>\mathbf{u}_{\theta}= \cos\theta\mathbf{u}_{\rho}-\mathrm{sen}\,\theta\mathbf{u}_{z}</math></center>
 +
 +
Sin embargo, es importante que recordar que <math>\theta</math> no tiene un valor arbitrario, sino el correspondiente al punto en que se evalúan los vectores.
 +
 +
Para este punto tenemos que
 +
 +
<center><math>x=3\,</math>{{qquad}}<math>y = 4\,</math>{{qquad}}<math>z=12\,</math></center>
 +
 +
 +
<center><math>\rho = \sqrt{x^2+y^2} = 5</math>{{qquad}}<math>r = \sqrt{x^2+y^2+z^2}=13</math></center>
 +
 +
y de aquí
 +
 +
<center><math>\mathrm{sen}\,\theta = \frac{\rho}{r}= \frac{5}{13}</math>{{qquad}}
 +
<math>\cos\theta = \frac{z}{r} = \frac{12}{13}</math></center>
 +
 +
 +
<center><math>\mathbf{u}_{r}=\frac{5}{13}\mathbf{u}_{\rho}+\frac{12}{13}\mathbf{u}_{z}</math>{{qquad}}
 +
<math>\mathbf{u}_{\theta}=\frac{12}{13}\mathbf{u}_{\rho}-\frac{5}{13}5\mathbf{u}_{z}</math></center>
 +
 +
De estas relaciones tenemos que
 +
 +
<center><math>\mathbf{B} = 5\mathbf{u}_{r}+12\mathbf{u}_{z} =
 +
\frac{5^2+12^2}{13}\mathbf{u}_{\rho}+\frac{5{\cdot}12-12{\cdot}5}{13}\mathbf{u}_{z}= 13\mathbf{u}_{\rho}</math></center>
 +
 +
y las operaciones buscadas son
===Suma===
===Suma===
 +
 +
La suma de estos dos vectores es
 +
 +
<center><math>\mathbf{A}+\mathbf{B} = 14\mathbf{u}_{\rho}-\mathbf{u}_{z}</math></center>
===Producto escalar===
===Producto escalar===
 +
Expresados los dos vectores en la misma base, el producto escalar es la suma de los productos de las componentes correspondientes.
 +
 +
<center><math>\mathbf{A}{\cdot}\mathbf{B} = 13</math></center>
 +
 +
Este producto escalar puede calcularse también sin necesidad de pasar una base común, pero requiere conocer los productos escalares de las diferentes bases.
 +
 +
<center><math>\mathbf{A}{\cdot}\mathbf{B} =
 +
5\mathbf{u}_{\rho}{\cdot}\mathbf{u}_{r}-5\mathbf{u}_{z}{\cdot}\mathbf{u}_{r}+12\mathbf{u}_{\rho}{\cdot}\mathbf{u}_{\theta}-12\mathbf{u}_{z}{\cdot}\mathbf{u}_{\theta}</math></center>
 +
 +
[[Imagen:angulo-bases.gif|left]]El producto escalar de dos vectores unitarios es igual al coseno del ángulo que forman. En el caso de <math>\mathbf{u}_{r}</math> y <math>\mathbf{u}_{z}</math>, éste es justamente <math>\theta</math>, por la definición de este ángulo. Por tanto
 +
 +
<center><math>\mathbf{u}_{r}{\cdot}\mathbf{u}_{z}=\cos\theta = \frac{12}{13}</math>{{qquad}}<math>\mathbf{u}_{r}{\cdot}\mathbf{u}_{\rho}=\mathrm{sen}\,\theta = \frac{5}{13}</math></center>
 +
 +
<center><math>\mathbf{u}_{\theta}{\cdot}\mathbf{u}_{z}=-\mathrm{sen}\,\theta = -\frac{5}{13}</math>{{qquad}}<math>\mathbf{u}_{\theta}{\cdot}\mathbf{u}_{\rho}=\cos\theta = \frac{12}{13}</math></center>
 +
 +
y el producto escalar de <math>\mathbf{A}</math> y <math>\mathbf{B}</math> es
 +
 +
<center><math>\mathbf{A}{\cdot}\mathbf{B} = 5\frac{5}{13}-5\frac{12}{13}+12\frac{12}{13}+12\frac{5}{13}=
 +
\frac{169}{13}=13</math></center>
===Producto vectorial===
===Producto vectorial===
 +
El producto vectorial vale
 +
 +
<center>
 +
<math>\mathbf{A}\times\mathbf{B} = (\mathbf{u}_{\rho}-\mathbf{u}_{z})\times(13\mathbf{u}_{\rho}) =
 +
13\mathbf{u}_{\rho}\times\mathbf{u}_{\rho}-13\mathbf{u}_{z}\times\mathbf{u}_{\rho}=-13\mathbf{u}_{\varphi}</math></center>
 +
 +
Este producto puede hacerse también sin reducir los vectores a una base común, calculando los productos vectoriales entre las diferentes bases.
 +
[[Categoría:Problemas de fundamentos matemáticos]]
[[Categoría:Problemas de fundamentos matemáticos]]

última version al 19:44 27 sep 2010

Contenido

1 Enunciado

Dados los vectores

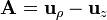
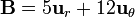
\mathbf{A} = \mathbf{u}_{\rho}-\mathbf{u}_{z}     \mathbf{B} = 5\mathbf{u}_{r}+12\mathbf{u}_{\theta}

evaluados en el punto de coordenadas cartesianas x = 3, y = 4, z = 12, calcule

  1. \mathbf{A}+\mathbf{B}\,
  2. \mathbf{A}{\cdot}\mathbf{B}\,
  3. \mathbf{A}\times\mathbf{B}\,

2 Solución

La única complicación de este problema consiste en expresar ambos vectores en la misma base, ya que, aunque se encuentran evaluados en el mismo punto, uno se encuentra en la base de esféricas y el otro en la de cilíndricas.

Para operar conviene reducirlos a una base común. Ésta no tiene por qué ser la base cartesiana, sino que nos vale la cilíndrica o la esférica (o, cualquier otra, en realidad).

Si empleamos la base de cilíndricas, tenemos que

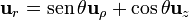
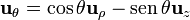
\mathbf{u}_{r}=\mathrm{sen}\,\theta \mathbf{u}_{\rho}+\cos\theta\mathbf{u}_{z}     \mathbf{u}_{\theta}= \cos\theta\mathbf{u}_{\rho}-\mathrm{sen}\,\theta\mathbf{u}_{z}

Sin embargo, es importante que recordar que θ no tiene un valor arbitrario, sino el correspondiente al punto en que se evalúan los vectores.

Para este punto tenemos que

x=3\,    y = 4\,    z=12\,


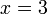
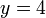
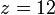
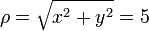
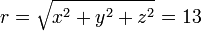
\rho = \sqrt{x^2+y^2} = 5    r = \sqrt{x^2+y^2+z^2}=13

y de aquí

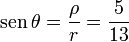
\mathrm{sen}\,\theta = \frac{\rho}{r}= \frac{5}{13}     \cos\theta = \frac{z}{r} = \frac{12}{13}


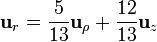
\mathbf{u}_{r}=\frac{5}{13}\mathbf{u}_{\rho}+\frac{12}{13}\mathbf{u}_{z}     \mathbf{u}_{\theta}=\frac{12}{13}\mathbf{u}_{\rho}-\frac{5}{13}5\mathbf{u}_{z}

De estas relaciones tenemos que

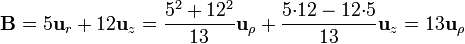
\mathbf{B} = 5\mathbf{u}_{r}+12\mathbf{u}_{z} = \frac{5^2+12^2}{13}\mathbf{u}_{\rho}+\frac{5{\cdot}12-12{\cdot}5}{13}\mathbf{u}_{z}= 13\mathbf{u}_{\rho}

y las operaciones buscadas son

2.1 Suma

La suma de estos dos vectores es

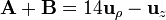
\mathbf{A}+\mathbf{B} = 14\mathbf{u}_{\rho}-\mathbf{u}_{z}

2.2 Producto escalar

Expresados los dos vectores en la misma base, el producto escalar es la suma de los productos de las componentes correspondientes.

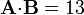
\mathbf{A}{\cdot}\mathbf{B} = 13

Este producto escalar puede calcularse también sin necesidad de pasar una base común, pero requiere conocer los productos escalares de las diferentes bases.

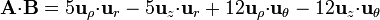
\mathbf{A}{\cdot}\mathbf{B} = 5\mathbf{u}_{\rho}{\cdot}\mathbf{u}_{r}-5\mathbf{u}_{z}{\cdot}\mathbf{u}_{r}+12\mathbf{u}_{\rho}{\cdot}\mathbf{u}_{\theta}-12\mathbf{u}_{z}{\cdot}\mathbf{u}_{\theta}
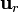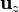El producto escalar de dos vectores unitarios es igual al coseno del ángulo que forman. En el caso de \mathbf{u}_{r} y \mathbf{u}_{z}, éste es justamente θ, por la definición de este ángulo. Por tanto
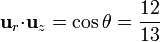
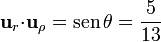
\mathbf{u}_{r}{\cdot}\mathbf{u}_{z}=\cos\theta = \frac{12}{13}    \mathbf{u}_{r}{\cdot}\mathbf{u}_{\rho}=\mathrm{sen}\,\theta = \frac{5}{13}
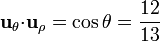
\mathbf{u}_{\theta}{\cdot}\mathbf{u}_{z}=-\mathrm{sen}\,\theta = -\frac{5}{13}    \mathbf{u}_{\theta}{\cdot}\mathbf{u}_{\rho}=\cos\theta = \frac{12}{13}

y el producto escalar de \mathbf{A} y \mathbf{B} es

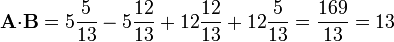
\mathbf{A}{\cdot}\mathbf{B} = 5\frac{5}{13}-5\frac{12}{13}+12\frac{12}{13}+12\frac{5}{13}= \frac{169}{13}=13

2.3 Producto vectorial

El producto vectorial vale

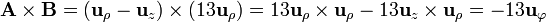
\mathbf{A}\times\mathbf{B} = (\mathbf{u}_{\rho}-\mathbf{u}_{z})\times(13\mathbf{u}_{\rho}) = 13\mathbf{u}_{\rho}\times\mathbf{u}_{\rho}-13\mathbf{u}_{z}\times\mathbf{u}_{\rho}=-13\mathbf{u}_{\varphi}

Este producto puede hacerse también sin reducir los vectores a una base común, calculando los productos vectoriales entre las diferentes bases.

Obtenido de "http://tesla.us.es/wiki/index.php/Operaciones_con_vectores_en_diferentes_sistemas"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 19:44, 27 sep 2010. - Esta página ha sido visitada 7.109 veces. - Aviso legal - Acerca de Laplace