Campo de distribuciones con simetría esférica
De Laplace
(→Introducción) |
(→Una esfera maciza cargada uniformemente) |
||
| (6 ediciones intermedias no se muestran.) | |||
| Línea 54: | Línea 54: | ||
==Una carga puntual== | ==Una carga puntual== | ||
| + | [[Archivo:flujo-carga-puntual.png|right]] | ||
| + | |||
El sistema más simple es el de una carga puntual. En este caso, todas las superficies esféricas concéntricas envuelven la misma carga | El sistema más simple es el de una carga puntual. En este caso, todas las superficies esféricas concéntricas envuelven la misma carga | ||
| Línea 72: | Línea 74: | ||
<center><math>\vec{E}=\frac{1}{4\pi\varepsilon_0}\,\frac{Q}{r^2}\vec{u}_r\qquad (r>R)</math></center> | <center><math>\vec{E}=\frac{1}{4\pi\varepsilon_0}\,\frac{Q}{r^2}\vec{u}_r\qquad (r>R)</math></center> | ||
| + | |||
| + | <center>[[Archivo:flujo-superficie-esferica-01.png]]{{qquad}}{{qquad}}[[Archivo:flujo-superficie-esferica-02.png]]</center> | ||
;Punto interior: Si tomamos una superficie esférica concéntrica con la de la carga, pero interior a ella, la carga que encerramos es nula | ;Punto interior: Si tomamos una superficie esférica concéntrica con la de la carga, pero interior a ella, la carga que encerramos es nula | ||
| Línea 117: | Línea 121: | ||
<center><math>Q_\mathrm{int}=+Q-Q=0\qquad (r > b)\qquad\Rightarrow\qquad \vec{E}=\vec{0}\qquad (r > b)</math></center> | <center><math>Q_\mathrm{int}=+Q-Q=0\qquad (r > b)\qquad\Rightarrow\qquad \vec{E}=\vec{0}\qquad (r > b)</math></center> | ||
| + | |||
| + | <center>[[Archivo:flujo-dos-superficies-01.png]]{{qquad}}[[Archivo:flujo-dos-superficies-02.png]]{{qquad}}[[Archivo:flujo-dos-superficies-03.png]]</center> | ||
Reuniendo los tres resultados | Reuniendo los tres resultados | ||
| Línea 180: | Línea 186: | ||
[[Archivo:Dependenciacampoesfera.gif|right]]Reuniendo las dos expresiones en su forma más usual | [[Archivo:Dependenciacampoesfera.gif|right]]Reuniendo las dos expresiones en su forma más usual | ||
| - | <center><math>\vec{E}=\begin{cases} \displaystyle \frac{\rho_0}{3\varepsilon_0}\vec{r} & r < R \\ & \\ \displaystyle\frac{Q}{4\pi\varepsilon_0 r^2}\vec{u}_r & r > R \end{cases}</math></center> | + | <center><math>\vec{E}=\begin{cases} \displaystyle \frac{\rho_0}{3\varepsilon_0}\vec{r} & r < R \\ & \\ \displaystyle\frac{Q}{4\pi\varepsilon_0 r^2}\vec{u}_r & r > R \end{cases}=\begin{cases} \displaystyle \frac{Qr}{4\pi\varepsilon_0R^3}\vec{u}_r & r < R \\ & \\ \displaystyle\frac{Q}{4\pi\varepsilon_0 r^2}\vec{u}_r & r > R \end{cases}</math></center> |
Las dos pueden escribirse en términos de la carga total o de la densidad de carga sin más que sustituir la relación anterior | Las dos pueden escribirse en términos de la carga total o de la densidad de carga sin más que sustituir la relación anterior | ||
<center><math>\rho_0=\frac{Q}{4\pi R^3/3}=\frac{3Q}{4\pi R^3}</math></center> | <center><math>\rho_0=\frac{Q}{4\pi R^3/3}=\frac{3Q}{4\pi R^3}</math></center> | ||
| - | |||
| - | |||
==Una esfera con densidad no uniforme== | ==Una esfera con densidad no uniforme== | ||
| Línea 212: | Línea 216: | ||
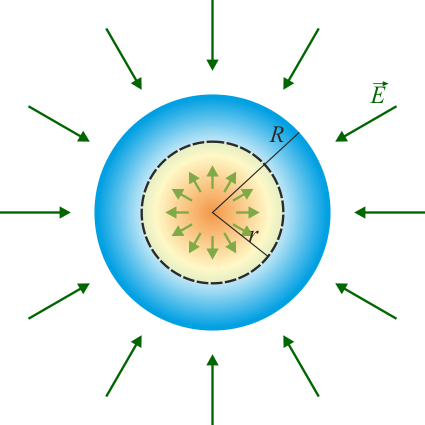
<center><math>\vec{E}=\frac{Q_\mathrm{int}(r)}{4\pi\varepsilon_0 r^2}\vec{u}_r = \frac{A r(2R-3r)}{6\varepsilon_0}\vec{u}_r\qquad (r < R)</math></center> | <center><math>\vec{E}=\frac{Q_\mathrm{int}(r)}{4\pi\varepsilon_0 r^2}\vec{u}_r = \frac{A r(2R-3r)}{6\varepsilon_0}\vec{u}_r\qquad (r < R)</math></center> | ||
| + | |||
| + | <center>[[Archivo:esfera-densidad-radial-02.png]]{{qquad}}[[Archivo:esfera-densidad-radial-03.png]]</center> | ||
;Punto exterior: En este caso hay que tener en cuenta que la densidad de carga “se acaba” al llegar a <math>r=R</math>. En el exterior de la esfera no hay carga, por lo que si consideramos una superficie con <math>r >R</math> la carga encerrada es toda la que hay | ;Punto exterior: En este caso hay que tener en cuenta que la densidad de carga “se acaba” al llegar a <math>r=R</math>. En el exterior de la esfera no hay carga, por lo que si consideramos una superficie con <math>r >R</math> la carga encerrada es toda la que hay | ||
| Línea 221: | Línea 227: | ||
<center><math>\vec{E}=\frac{Q_\mathrm{int}(r)}{4\pi\varepsilon_0 r^2}\vec{u}_r = -\frac{A R^4}{6\varepsilon_0 r^2}\vec{u}_r\qquad (r > R)</math></center> | <center><math>\vec{E}=\frac{Q_\mathrm{int}(r)}{4\pi\varepsilon_0 r^2}\vec{u}_r = -\frac{A R^4}{6\varepsilon_0 r^2}\vec{u}_r\qquad (r > R)</math></center> | ||
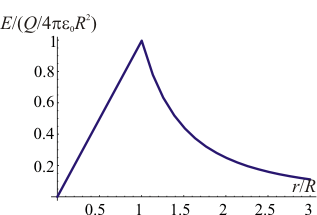
| + | [[Archivo:dependencia-esfera-no-uniforme.png|right]]La gráfica de la dependencia del campo eléctrico con la distancia al centro es más complicada que en los casos anteriores. En el interior el campo sigue una dependencia parabólica. Cerca del centro, cargado positivamente, el campo va hacia al exterior (signo positivo en la gráfica), a medida que nos alejamos, el campo de la carga negativa compensa el de la positiva (a una distancia <math>r = 2R/3</math> en que el campo se anula) y a partir de ahí lo supera, produciendo un campo hacia adentro (signo negativo en la gráfica). Para <math>r > R</math> tenemos el decaimiento como la inversa del cuadrado, característica de una una carga puntual, negativa en este caso. | ||
[[Categoría:Problemas de electrostática en el vacío (GIE)]] | [[Categoría:Problemas de electrostática en el vacío (GIE)]] | ||
última version al 12:08 29 oct 2013
Contenido |
1 Enunciado
Con ayuda de la ley de Gauss, calcule el campo eléctrico en todos los puntos del espacio para las siguientes distribuciones con simetría esférica:
- Una carga puntual q.
- Una superficie esférica de radio a que almacena una carga Q distribuida uniformemente.
- Dos superficies esféricas concéntricas, de radios a y b (a < b) que almacenan respectivamente cargas + Q y − Q, distribuidas uniformemente.
- Dos superficies esféricas concéntricas, de radios a y b (a < b) cargadas respectivamente con densidades superficiales uniformes + σ0 y − σ0.
- Una esfera maciza de radio R que almacena una carga Q distribuida uniformemente en su volumen.
- Una esfera maciza de radio R con una densidad de carga dependiente de la distancia al centro como
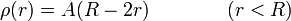
2 Introducción
La ley de Gauss establece que el flujo del campo eléctrico a través de una superficie cerrada es proporcional a la carga encerrada en su interior
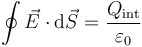
siendo  una constante universal conocida como permitividad del vacío.
una constante universal conocida como permitividad del vacío.
La ley de Gauss, aunque siempre es cierta, no siempre es útil como herramienta para hallar el campo eléctrico. La razón es que del valor de una integral definida no se deduce el valor del integrando (existen infinitas funciones diferentes que tienen la misma integral definida en un dominio dado).
Existe un caso, no obstante, en que la ley de Gauss permite obtener el campo eléctrico. Si la distribución de carga posee simetría esférica o de revolución, de manera que se ve igual desde todas las direcciones, el campo eléctrico que produce va en la dirección radial y depende solo de la distancia al centro de la distribución
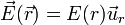
Este es el caso, por ejemplo, de una carga puntual. La cantidad E(r) no es el módulo del campo, sino su componente radial, ya que tiene un signo que nos dice si va hacia afuera (caso de una carga positiva) o hacia adentro (caso de una carga negativa).
Hay que remarcar que no todas las distribuciones de carga en una esfera poseen simetría esférica. Por ejemplo, una esfera cargada positivamente en su hemisferio “norte” y negativamente en el “sur” no posee simetría esférica, ya que no todas las direcciones son equivalentes. No se ve lo mismo desde el norte que desde el sur o desde el ecuador.
Suponiendo que sí existe simetría esférica, el flujo del campo eléctrico a través de una superficie esférica puede hallarse explícitamente. Si toamos una superficie esférica de radio r concéntrica con la distribución, el diferencial de superficie, ortogonal a ésta, va en la dirección radial
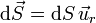
Por ello, el flujo se reduce a una integral de un escalar
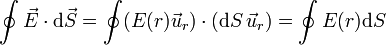
Ahora bien, dado que la superficie de integración es una esfera, todos sus puntos se encuentran a la misma distancia del centro y por tanto, el valor de la componente radial del campo, E(r), tiene el mismo valor para todos ellos y puede extraerse de la integral
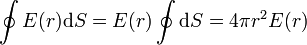
Hay que recordar que el campo no es el mismo para todos los puntos de la superficie esférica, ya que su dirección y sentido cambian de un punto a otro. Lo que es constante es el valor de su módulo.
Llevando esto a la ley de Gauss nos queda
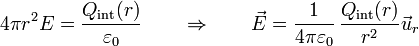
Por tanto, para los sistemas con simetría esférica (y solo para ellos) el campo para cada distancia del centro equivale al de una carga puntual cuyo valor es igual al de toda la carga contenida en el volumen r' < r.
Para analizar las distribuciones siguientes solo hay que hallar Qint(r) en cada caso.
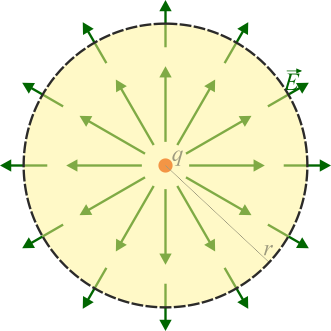
3 Una carga puntual
El sistema más simple es el de una carga puntual. En este caso, todas las superficies esféricas concéntricas envuelven la misma carga
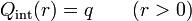
y el campo producido por la carga vale

4 Una superficie esférica
Para una superficie esférica cargada tenemos dos casos: un punto en el volumen interior, o en el exterior.
- Punto exterior
- Si consideramos una superficie esférica de radio r > R, la carga contenida por ella es toda la de la esfera,

- por lo que
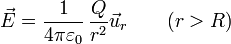
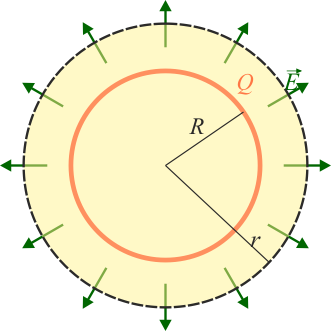
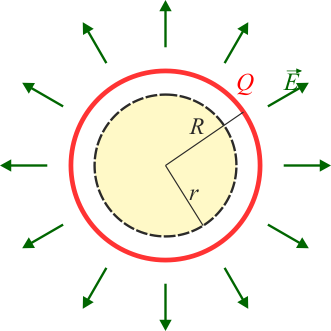
- Punto interior
- Si tomamos una superficie esférica concéntrica con la de la carga, pero interior a ella, la carga que encerramos es nula

- por lo que el campo en el interior de la esfera es nulo

Reuniendo los dos resultados
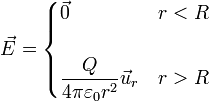
Puesto que la ley de Gauss es aplicable también al campo gravitatorio, esto quiere decir que en un hipotético planeta hueco, el campo gravitatorio sería nulo, es decir que no podría haber habitantes caminando por el interior, pegados al suelo por el otro lado, sino que en todo caso flotarían en el interior.
El campo eléctrico de una superficie cargada posee un salto en la superficie, como ocurre siempre que hay una superficie cargada. El valor del salto es

donde
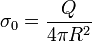
es la densidad de carga en la superficie de la esfera.
5 Dos superficies concéntricas con cargas opuestas
Para el caso de dos superficies esféricas podemos o bien aplicar el principio de superposición, empleando el resultado del apartado anterior, o bien aplicar directamente la ley de Gauss a la distribución completa.
Si optamos por lo segundo tenemos tres posibilidades según estemos en la región interior, la intermedia o la exterior.
- Región interior
- Para r < a la carga encerrada es nula
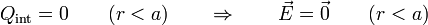
- Región intermedia
- Una superficie situada entre las dos esferas de carga contiene a la más pequeña, pero no a la grande
- Región exterior
- Una superficie por fuera de la esfera mayor contiene tanto a la carga de ésta como a la de la esfera pequeña
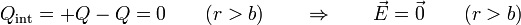
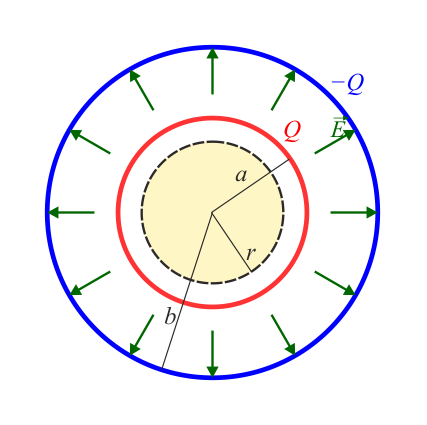
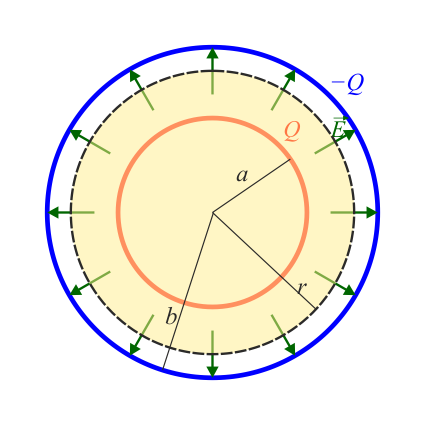
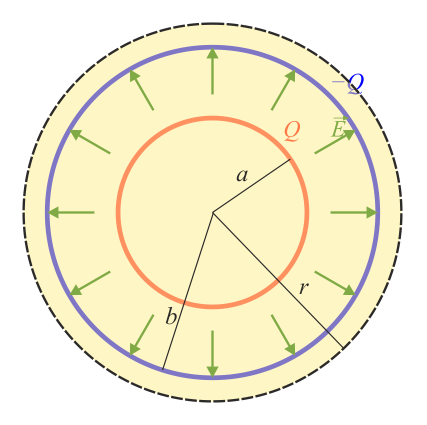
Reuniendo los tres resultados
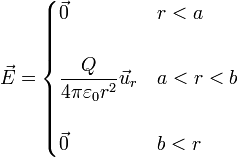
En este caso, el campo presenta dos discontinuidades, una en cada superficie de carga.
6 Dos superficies concéntricas con densidades opuestas
Este puede se parece al anterior, pero no es equivalente. Las dos esferas tienen cargas de signo opuesto, pero su valor es diferente, al serlo el área de cada una. Las cargas respectivas valen

Aplicando el mismo razonamiento que en el apartado anterior
- Región interior
- Para r < a la carga encerrada es nula
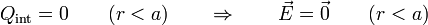
- Región intermedia
- En a < r < b solo se contiene a la carga de la esfera menor

- Región exterior
- Una superficie por fuera de la esfera mayor contiene tanto a la carga de las dos esferas

Reuniendo los tres resultados
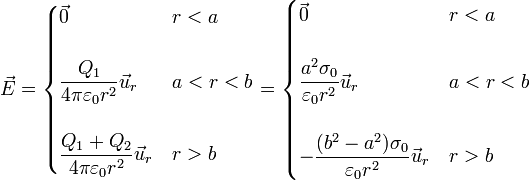
El campo presenta de nuevo dos discontinuidades. En este caso no se anula el campo en el exterior porque el sistema posee carga neta.
7 Una esfera maciza cargada uniformemente
Una esfera maciza cargada uniformemente posee una densidad volumétrica de carga igual a
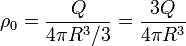
En este caso, todas las superficies contienen algo de carga, que depende de qué radio tomemos. Tenemos dos casos,
- Punto exterior
- Si consideramos una superficie esférica de radio r > R, la carga contenida por ella es toda la de la esfera,

- por lo que
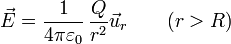
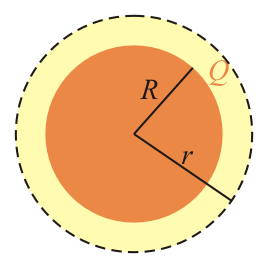
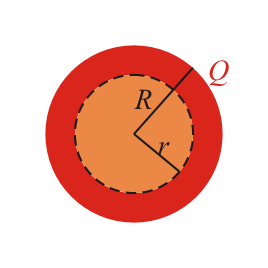
- Punto interior
- Si tomamos una superficie esférica concéntrica con la de la carga, pero interior a ella, la carga que encerramos depende del radio considerado, ya que solo abarcamos parte de la carga de la esfera
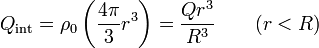
- por lo que el campo en el interior de la esfera vale
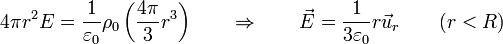
- Vemos que el campo eléctrico en el interior de la esfera aumenta linealmente con la distancia, siendo nulo solo en su centro. Puede escribirse en función del vector de posición
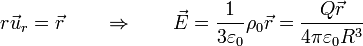
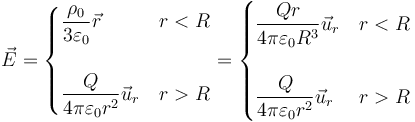
Las dos pueden escribirse en términos de la carga total o de la densidad de carga sin más que sustituir la relación anterior
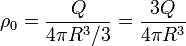
8 Una esfera con densidad no uniforme
Cuando tenemos una densidad variable es necesario hallar de forma integral la cantidad de carga encerrada.
Consideramos una superficie esférica de radio r concéntrica con la distribución. La cantidad de carga que contiene será igual a la integral de la densidad de carga
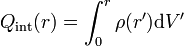
Como elementos de volumen consideramos campas esféricas de espesor dr', siendo el diferencial de volumen el producto del área por el espesor
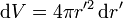
lo que nos da la integral

Para el caso de la densidad de carga del enunciado tenemos de nuevo dos casos:
- Punto interior
- La integral abarca parte de la carga total, siendo valor
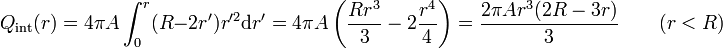
- siendo el campo
- Punto exterior
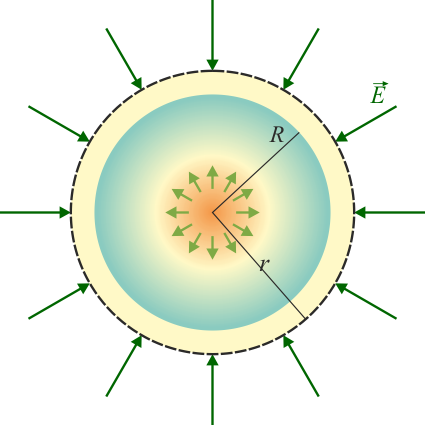
- En este caso hay que tener en cuenta que la densidad de carga “se acaba” al llegar a r = R. En el exterior de la esfera no hay carga, por lo que si consideramos una superficie con r > R la carga encerrada es toda la que hay

- siendo el campo exterior el de una carga puntual negativa