Comparación de dos producciones de entropía
De Laplace
m (→Agua fría en tanque caliente) |
|||
| (7 ediciones intermedias no se muestran.) | |||
| Línea 2: | Línea 2: | ||
Halle la variación de entropía del sistema, del ambiente y del universo en los dos casos siguientes: | Halle la variación de entropía del sistema, del ambiente y del universo en los dos casos siguientes: | ||
| - | |||
# Se vierte un litro de agua a 80°C en una piscina a 20°C. | # Se vierte un litro de agua a 80°C en una piscina a 20°C. | ||
| + | # Se vierte un litro de agua a 20°C en una piscina a 80°C. | ||
==Solución general== | ==Solución general== | ||
| Línea 38: | Línea 38: | ||
La variación de entropía cuando el agua pasa de una temperatura <math>T</math> a una <math>T + dT</math> es | La variación de entropía cuando el agua pasa de una temperatura <math>T</math> a una <math>T + dT</math> es | ||
| - | <center><math>\mathrm{d}S = \frac{\ | + | <center><math>\mathrm{d}S = \frac{\delta Q^\mathrm{rev}}{T}= \frac{mc_p\,\mathrm{d}T}{T}</math></center> |
Si suponemos que el calor específico no depende de la temperatura, podemos integrar esta ecuación y obtener el incremento de entropía | Si suponemos que el calor específico no depende de la temperatura, podemos integrar esta ecuación y obtener el incremento de entropía | ||
| Línea 54: | Línea 54: | ||
En el primer caso | En el primer caso | ||
| - | <center><math>T_i = 353\,\mathrm{K}</math>{{qquad}}{{qquad}}<math> | + | <center><math>T_i = 353\,\mathrm{K}</math>{{qquad}}{{qquad}}<math>T_f = 293\,\mathrm{K}</math>{{qquad}}{{qquad}}<math>m=1.0\,\mathrm{kg}</math>{{qquad}}{{qquad}}<math>c_p=4.18\,\frac{\mathrm{kJ}}{\mathrm{kg}\cdot\mathrm{K}}</math></center> |
lo que nos da para la variación de entropía del sistema | lo que nos da para la variación de entropía del sistema | ||
| - | <center><math>\Delta S_\mathrm{sis} = mc_p \ln\left(\frac{T_f}{T_i}\right) = - | + | <center><math>\Delta S_\mathrm{sis} = mc_p \ln\left(\frac{T_f}{T_i}\right) = -778\,\frac{\mathrm{J}}{\mathrm{K}}</math></center> |
Para el ambiente es | Para el ambiente es | ||
| - | <center><math>\Delta S_\mathrm{amb}=\frac{mc_p(T_i-T_f)}{T_f}=+ | + | <center><math>\Delta S_\mathrm{amb}=\frac{mc_p(T_i-T_f)}{T_f}=+856\,\frac{\mathrm{J}}{\mathrm{K}}</math></center> |
La del universo es | La del universo es | ||
| - | <center><math>\Delta S_\mathrm{u}=\Delta S_\mathrm{amb}+\Delta S_\mathrm{sis} = + | + | <center><math>\Delta S_\mathrm{u}=\Delta S_\mathrm{amb}+\Delta S_\mathrm{sis} = +78\,\frac{\mathrm{J}}{\mathrm{K}}</math></center> |
La variación de la entropía es positiva, como corresponde a un proceso irreversible. El sistema reduce su entropía al enfriarse, pero al ambiente ve incrementada la suya en una cantidad mayor. | La variación de la entropía es positiva, como corresponde a un proceso irreversible. El sistema reduce su entropía al enfriarse, pero al ambiente ve incrementada la suya en una cantidad mayor. | ||
| Línea 73: | Línea 73: | ||
En el segundo caso | En el segundo caso | ||
| - | <center><math>T_i = 293\,\mathrm{K}</math>{{qquad}}{{qquad}}<math> | + | <center><math>T_i = 293\,\mathrm{K}</math>{{qquad}}{{qquad}}<math>T_f = 353\,\mathrm{K}</math>{{qquad}}{{qquad}}<math>m=1\,\mathrm{kg}</math>{{qquad}}{{qquad}}<math>c_p=4.18\,\frac{\mathrm{kJ}}{\mathrm{kg}\cdot\mathrm{K}}</math></center> |
| - | }}{\mathrm{ | + | |
lo que nos da para la variación de entropía del sistema | lo que nos da para la variación de entropía del sistema | ||
| - | <center><math>\Delta S_\mathrm{sis} = mc_p \ln\left(\frac{T_f}{T_i}\right) = + | + | <center><math>\Delta S_\mathrm{sis} = mc_p \ln\left(\frac{T_f}{T_i}\right) = +778\,\frac{\mathrm{J}}{\mathrm{K}}</math></center> |
Esta es igual a la del caso anterior, pero cambiada de signo. Esto está de acuerdo con que se trata del mismo proceso reversible recorrido en sentido contrario. | Esta es igual a la del caso anterior, pero cambiada de signo. Esto está de acuerdo con que se trata del mismo proceso reversible recorrido en sentido contrario. | ||
| Línea 84: | Línea 83: | ||
Para el ambiente es ahora | Para el ambiente es ahora | ||
| - | <center><math>\Delta S_\mathrm{amb}=\frac{mc_p(T_i-T_f)}{T_f}=- | + | <center><math>\Delta S_\mathrm{amb}=\frac{mc_p(T_i-T_f)}{T_f}=-710\,\frac{\mathrm{J}}{\mathrm{K}}</math></center> |
que es ''diferente'' de la del caso anterior (el denominador es distinto). | que es ''diferente'' de la del caso anterior (el denominador es distinto). | ||
| Línea 90: | Línea 89: | ||
La del universo es en este caso | La del universo es en este caso | ||
| - | <center><math>\Delta S_\mathrm{u}=\Delta S_\mathrm{amb}+\Delta S_\mathrm{sis} = + | + | <center><math>\Delta S_\mathrm{u}=\Delta S_\mathrm{amb}+\Delta S_\mathrm{sis} = +68\,\frac{\mathrm{J}}{\mathrm{K}}</math></center> |
La variación de la entropía vuelve a ser ''positiva'', ya que de nuevo tenemos un proceso irreversible. El sistema aumenta su entropía al calentarse, y la reducción en la entropía del ambiente es más pequeña. | La variación de la entropía vuelve a ser ''positiva'', ya que de nuevo tenemos un proceso irreversible. El sistema aumenta su entropía al calentarse, y la reducción en la entropía del ambiente es más pequeña. | ||
[[Categoría:Problemas del segundo principio de la termodinámica (GIE)]] | [[Categoría:Problemas del segundo principio de la termodinámica (GIE)]] | ||
última version al 11:06 24 jul 2019
Contenido |
1 Enunciado
Halle la variación de entropía del sistema, del ambiente y del universo en los dos casos siguientes:
- Se vierte un litro de agua a 80°C en una piscina a 20°C.
- Se vierte un litro de agua a 20°C en una piscina a 80°C.
2 Solución general
Los dos fenómenos son del mismo tipo: una cierta cantidad de sustancia a una temperatura Ti es puesta en contacto con un baño térmico a una temperatura Tf. Como resultado, la temperatura de la sustancia cambia hasta igualarse con la del baño. En el proceso se produce una transferencia de calor y una variación en la entropía del universo.
Para hallar esta variación separamos en la variación de la entropía del sistema, del baño y la total.
2.1 Variación de entropía del ambiente
Cuando el agua del sistema se enfría o se calienta intercambia una cierta cantidad de calor igual a
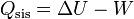
Puesto que el proceso ocurre a presión constante, el trabajo realizado sobre el sistema no es nulo, sino que vale − pΔV. Para incluirlo en los cálculos, en lugar de la energía interna usamos la entalpía H = U + pV. A presión constante, el calor equivale a la variación de la entalpía, y es proporcional a la variación de la temperatura
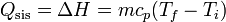
siendo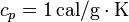 
el calor específico del agua (por unidad de masa).
Este calor es negativo si el sistema se enfría (pues en realidad sale del sistema) y positivo si se calienta.
El calor que entra en el ambiente es este mismo, cambiado de signo
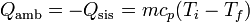
Esta entrada de calor se produce a una temperatura constante (en el ambiente) Tf, por lo que el aumento de entropía del ambiente es
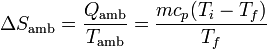
2.2 Variación de entropía del sistema
El proceso que se describe en este ejemplo es irreversible, ya que se debe a una cesión de calor debida a una diferencia finita de temperaturas. Al verter el agua, el cambio de temperatura se producirá en general de una forma complicada. Sin embargo, al ser tanto el estado inicial como el final estados de equilibrio, podemos calcular la variación de entropía suponiendo un proceso reversible que conecte estos dos mismos estados.
Este proceso reversible sería una variación gradual y uniforme de la temperatura, de forma que en todo momento el agua vertida se supone en equilibrio térmico. Para realizar este proceso necesitaríamos una cantidad infinita de baños térmicos, cada uno a una temperatura ligeramente diferente al siguiente, de forma que situaríamos al agua en contacto sucesivo con cada uno de ellos. Por supuesto, este proceso es irrealizable en la práctica, pero nos basta para hallar el cambio de entropía.
La variación de entropía cuando el agua pasa de una temperatura T a una T + dT es
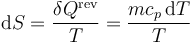
Si suponemos que el calor específico no depende de la temperatura, podemos integrar esta ecuación y obtener el incremento de entropía
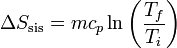
2.3 Variación de entropía total
Sumando las dos contribuciones obtenemos la variación de entropía total del universo.
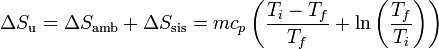
La fórmula puede aplicarse tanto al primer caso, de enfriamiento, como al segundo, de calentamiento. Puesto que los dos procesos parecen simétricos, podría pensarse que van a resultar iguales y de signo contrario. Veremos que no es así.
3 Agua caliente en tanque frío
En el primer caso
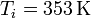
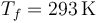
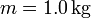
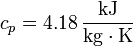
lo que nos da para la variación de entropía del sistema
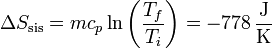
Para el ambiente es
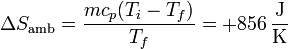
La del universo es
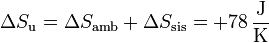
La variación de la entropía es positiva, como corresponde a un proceso irreversible. El sistema reduce su entropía al enfriarse, pero al ambiente ve incrementada la suya en una cantidad mayor.
4 Agua fría en tanque caliente
En el segundo caso
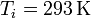
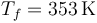
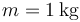
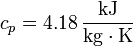
lo que nos da para la variación de entropía del sistema
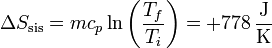
Esta es igual a la del caso anterior, pero cambiada de signo. Esto está de acuerdo con que se trata del mismo proceso reversible recorrido en sentido contrario.
Para el ambiente es ahora
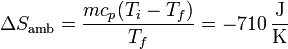
que es diferente de la del caso anterior (el denominador es distinto).
La del universo es en este caso
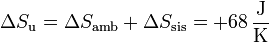
La variación de la entropía vuelve a ser positiva, ya que de nuevo tenemos un proceso irreversible. El sistema aumenta su entropía al calentarse, y la reducción en la entropía del ambiente es más pequeña.
