Cálculos de entropía (GIE)

De Laplace

(Diferencias entre revisiones)

última version al 13:52 30 may 2016

Contenido

1 Transferencia de calor
2 Cambio de fase
3 Calentamiento de una sustancia pura
4 Inmersión en un baño térmico
5 Gas ideal
6 Proceso adiabático irreversible
- 6.1 Experiencia de Joule
- 6.2 Compresión irreversible
7 Mezcla de gases
8 Reacciones químicas

1 Transferencia de calor

El caso más simple de producción de entropía se da cuando tenemos calor que pasa de un cuerpo caliente a uno frío. Si tenemos dos focos a temperaturas $T 1$ y $T 2$ y una cierta cantidad de calor $Q$ pasa del 1 al 2, se produce una disminución de entropía en el primero

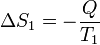
$\Delta S_1 = -\frac{Q}{T_1}$

y un aumento en el segundo

$\Delta S_2 = +\frac{Q}{T_2}$

resultando una variación neta en el universo

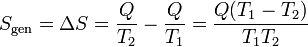
$S_\mathrm{gen}=\Delta S = \frac{Q}{T_2}-\frac{Q}{T_1}= \frac{Q(T_1-T_2)}{T_1T_2}$

Para que este proceso sea posible, debe ser $T 1 > T 2$ , como afirma el enunciado de Clausius.

Normalmente las temperaturas de los focos pueden estar cambiando en el tiempo (por ejemplo, un café que se va enfriando tiene una temperatura que se acerca exponencialmente a su valor final). En ese caso debemos considerar el ritmo al que se produce la entropía

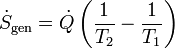
$\dot{S}_\mathrm{gen}=\dot{Q}\left(\frac{1}{T_2}-\frac{1}{T_1}\right)$

midiéndose el ritmo de producción en el SI en (J/K)/s = W/K.

Como modelo de cómo ocurre esta producción de entropía podemos considerar la conducción de calor. Si los dos focos térmicos están separados por una lámina conductora del calor, para la que se verifica la ley de Fourier

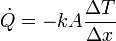
$\dot{Q}=-kA\frac{\Delta T}{\Delta x}$

estando uno de sus lados a una temperatura $T 1$ y el otro a temperatura $T 2$ . Aquí suponemos el sentido del flujo de calor del medio 1 al 2 y $Δ T = T 2 - T 1$ . En este caso el ritmo de producción de entropía

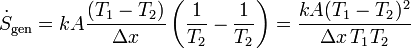
$\dot{S}_\mathrm{gen}= kA\frac{(T_1-T_2)}{\Delta x}\left(\frac{1}{T_2}-\frac{1}{T_2}\right) = \frac{kA(T_1-T_2)^2}{\Delta x\,T_1T_2}$

Por ejemplo, a través de una ventana cuyo exterior está a 15°C y cuyo interior a 22°C, siendo las dimensiones de la ventana 1.60×1.20 m² su espesor 5 mm y su conductividad térmica 0.96 W/m·K, el ritmo de producción de entropía es

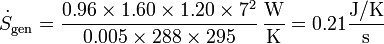
$\dot{S}_\mathrm{gen} = \frac{0.96\times 1.60\times 1.20\times 7^2}{0.005\times 288\times 295}\,\frac{\mathrm{W}}{\mathrm{K}} = 0.21\frac{\mathrm{J}/\mathrm{K}}{\mathrm{s}}$

2 Cambio de fase

Un cambio de fase es un proceso aproximadamente isotermo, por lo que la variación de la entropía de una sustancia cuando experimenta un cambio de fase es simplemente

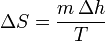
$\Delta S = \frac{m\,\Delta h}{T}$

siendo $Δ h$ la entalpía por unidad de masa del cambio de fase (de fusión o de vaporización, por ejemplo, para el agua).

Así, en el paso de hielo sólido a agua a 1 atm se produce un aumento de entropía por unidad de masa ( $s = S / m$ ):

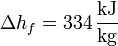
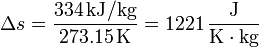
$\Delta h_f = 334\,\frac{\mathrm{kJ}}{\mathrm{kg}}$ $\Rightarrow$ $\Delta s = \frac{334\,\mathrm{kJ}/\mathrm{kg}}{273.15\,\mathrm{K}}=1221\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{kg}}$

y en el paso de agua a vapor de agua a 1 atm

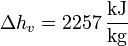
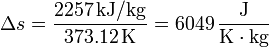
$\Delta h_v=2257\,\frac{\mathrm{kJ}}{\mathrm{kg}}$ $\Rightarrow$ $\Delta s = \frac{2257\,\mathrm{kJ}/\mathrm{kg}}{373.12\,\mathrm{K}}=6049\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{kg}}$

Vemos que es mucho mayor el aumento en la ebullición que en la fusión. Esto está asociado con el gran aumento del desorden al pasar de líquido a gas.

3 Calentamiento de una sustancia pura

Cuando se tiene una sustancia pura, como el agua, que experimenta una variación de su temperatura, siendo la presión inicial y la final la misma, la variación de la entropía de la sustancia es, según la definición

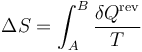
$\Delta S = \int_A^B \frac{\delta Q^\mathrm{rev}}{T}$

Como proceso reversible podemos imaginar uno en el que la temperatura de la sustancia va variando gradualmente por igual en todos sus puntos, siendo la presión siempre la misma. En este caso

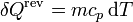
$\delta Q^\mathrm{rev} = mc_p\,\mathrm{d}T$

y la variación de entropía es

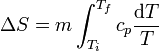
$\Delta S = m \int_{T_i}^{T_f}c_p\frac{\mathrm{d}T}{T}$

El calor específico es, en general, una función de la temperatura y debe ser tenido en cuenta a la hora de integrar. No obstante, si el rango de variación de la temperatura es pequeño, usualmente se puede aproximar $c p$ por una constante, su valor medio, y obtener la expresión

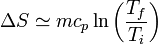
$\Delta S \simeq mc_p\ln\left(\frac{T_f}{T_i}\right)$

Combinado este resultado con el anterior, podemos trazar la gráfica de la entropía por unidad de masa, como función de la temperatura, para el agua desde el estado de hielo al de vapor, tomando como referencia el punto de fusión:

4 Inmersión en un baño térmico

Un caso frecuente de cálculo de entropía es aquel en que se tiene una sustancia pura, a una temperatura $T 1$ y se sumerge en un baño a temperatura $T 2$ , manteniéndose constante la presión. La sustancia se enfría (o se calienta, según el caso) hasta adaptarse a la temperatura del baño.

La variación de la entropía de la sustancia (si el calor específico se supone constante) es, según el apartado anterior

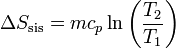
$\Delta S_\mathrm{sis}=mc_p\ln\left(\frac{T_2}{T_1}\right)$

La entropía del baño también cambia, pues absorbe calor a una temperatura constante. La cantidad de calor que se intercambia con el ambiente es

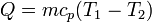
$Q = mc_p(T_1-T_2)\,$

Este calor sale del sistema y entra en el ambiente, por lo que la variación de entropía del baño es

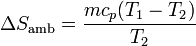
$\Delta S_\mathrm{amb}=\frac{mc_p(T_1-T_2)}{T_2}$

y la variación total de la entropía del universo será

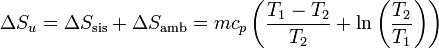
$\Delta S_u = \Delta S_\mathrm{sis}+\Delta S_\mathrm{amb}=mc_p\left(\frac{T_1-T_2}{T_2}+\ln\left(\frac{T_2}{T_1}\right)\right)$

Puede probarse de foma sencilla que, tanto si $T 1 > T 2$ como si $T 1 < T 2$ , esta variación es siempre positiva, esto es, el sistema siempre adquiere la temperatura del baño.

5 Gas ideal

Para un gas ideal podemos obtener una expresión válida para una presión y temperatura arbitrarias. Antes de dar una expresión general consideraremos algunos procesos característicos:

5.1 Expansión isoterma cuasiestática

Supongamos un gas ideal que se expande de manera reversible a temperatura constante $T A$ . En este caso se realiza un trabajo sobre el gas

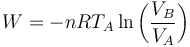
$W = -nRT_A\ln\left(\frac{V_B}{V_A}\right)$

Puesto que en este caso la energía interna no cambia, este trabajo debe ser compensado por una cantidad equivalente de calor

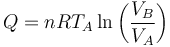
$Q = nRT_A\ln\left(\frac{V_B}{V_A}\right)$

Y, dado que el proceso es a temperatura constante, la variación de la entropía del gas vale

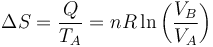
$\Delta S = \frac{Q}{T_A} = nR\ln\left(\frac{V_B}{V_A}\right)$

Si el gas se expande su entropía aumenta y si se comprime disminuye.

En términos de la presión, usando la ley de Boyle

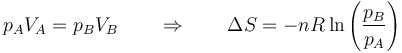
$p_AV_A=p_BV_B\qquad\Rightarrow\qquad \Delta S = -nR\ln\left(\frac{p_B}{p_A}\right)$

5.2 Calentamiento a volumen constante

Supongamos ahora una cierta cantidad de gas ideal que se va calentando gradualmente en un recipiente rígido. En este caso, el calor que entra en el gas para producir un incremento de temperaturas $d T$ vale

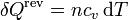
$\delta Q^\mathrm{rev} = nc_v\,\mathrm{d}T$

y la variación de entropía correspondiente es

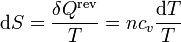
$\mathrm{d}S = \frac{\delta Q^\mathrm{rev}}{T}=nc_v\frac{\mathrm{d}T}{T}$

El incremento de entropía en una variación finita de temperatura es la suma de los diferenciales

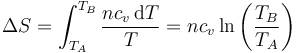
$\Delta S = \int_{T_A}^{T_B}\frac{nc_v\,\mathrm{d}T}{T}=nc_v\ln\left(\frac{T_B}{T_A}\right)$

Si la temperatura aumenta, también lo hace la entropía del gas y viceversa.

En términos de la presión, teniendo en cuenta que es a volumen constante,

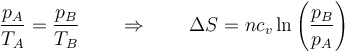
$\frac{p_A}{T_A}=\frac{p_B}{T_B}\qquad\Rightarrow\qquad \Delta S = nc_v\ln\left(\frac{p_B}{p_A}\right)$

5.3 Calentamiento a presión constante

Un cálculo análogo puede hacerse si suponemos un calentamiento gradual en el que la presión se mantiene constante (por ejemplo, permitiendo un émbolo que puede deslizarse por un cilindro). En este caso

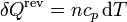
$\delta Q^\mathrm{rev} = nc_p\,\mathrm{d}T$

siendo el diferencial de entropía

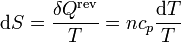
$\mathrm{d}S = \frac{\delta Q^\mathrm{rev}}{T}=nc_p\frac{\mathrm{d}T}{T}$

y su incremento

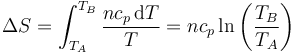
$\Delta S = \int_{T_A}^{T_B}\frac{nc_p\,\mathrm{d}T}{T}=nc_p\ln\left(\frac{T_B}{T_A}\right)$

De nuevo, si la temperatura aumenta, también lo hace la entropía del gas y viceversa. Puesto que $c p > c v$ en este caso el aumento de entropía es mayor que en el caso isócoro, ya que no solo aumenta la temperatura del gas, sino también el volumen que ocupa.

En términos del volumen, teniendo en cuenta que es a presión constante y se cumple la ley de Charles

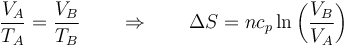
$\frac{V_A}{T_A}=\frac{V_B}{T_B}\qquad\Rightarrow\qquad \Delta S = nc_p\ln\left(\frac{V_B}{V_A}\right)$

5.4 Proceso general

Supongamos ahora una cantidad de gas que va de un estado en el que tiene una presión $p A$ , una temperatura $T A$ y ocupa un volumen $V A$ a uno en que tienen los valores $p B$ , $T B$ y $V B$ . El proceso para ir de uno a otro es arbitrario, puede ser cuasiestático o no serlo. El proceso no importa, ya que la entropía es una función de estado y para hallar su variación podemos elegir cualquier proceso reversible.

Podemos, por ejemplo, considerar un proceso en el que primero variamos su volumen, manteniendo su constante su presión $p A$ y posteriormente modificamos su presión a volumen constante $V B$ . Esto nos da la variación total de entropía

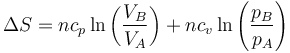
$\Delta S = nc_p\ln\left(\frac{V_B}{V_A}\right)+nc_v\ln\left(\frac{p_B}{p_A}\right)$

Esta es la expresión general de la variación de entropía de un gas ideal entre dos estados cualesquiera.

5.5 Expresiones alternativas

Con ayuda de la ley de los gases ideales podemos expresar la variación de entropía en términos de la presión y la temperatura, o de la temperatura y el volumen. Tenemos que

$\frac{p_BV_B}{T_B}=\frac{p_AV_A}{T_A}\qquad\Rightarrow\qquad \frac{p_B}{p_A}=\frac{T_B/T_A}{V_B/V_A}$

Sustituyendo y desarrollando el logaritmo

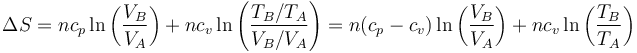
$\Delta S = nc_p\ln\left(\frac{V_B}{V_A}\right)+nc_v\ln\left(\frac{T_B/T_A}{V_B/V_A}\right) = n(c_p-c_v)\ln\left(\frac{V_B}{V_A}\right)+nc_v\ln\left(\frac{T_B}{T_A}\right)$

Aplicando la ley de Mayer

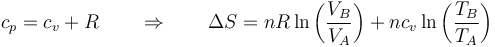
$c_p = c_v + R\qquad\Rightarrow\qquad \Delta S = nR\ln\left(\frac{V_B}{V_A}\right)+nc_v\ln\left(\frac{T_B}{T_A}\right)$

Si en lugar del cociente entre presiones hallamos el cociente entre volúmenes llegamos a

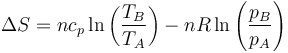
$\Delta S = nc_p\ln\left(\frac{T_B}{T_A}\right)-nR\ln\left(\frac{p_B}{p_A}\right)$

5.6 Relación con la fórmula de Gibbs

También podemos calcular la entropía de un gas ideal sin considerar proceso alguno, sin más que aplicar la identidad de Gibbs

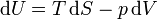
$\mathrm{d}U=T\,\mathrm{d}S-p\,\mathrm{d}V$

Despejando de aquí el diferencial de entropía

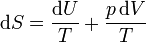
$\mathrm{d}S=\frac{\mathrm{d}U}{T}+\frac{p\,\mathrm{d}V}{T}$

Si sustituímos aquí las expresiones para la energía interna y la ley de los gases ideales

$\mathrm{d}U=nc_v\,\mathrm{d}T\qquad\qquad \frac{p}{T}=\frac{nR}{V}$

queda

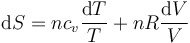
$\mathrm{d}S=nc_v\frac{\mathrm{d}T}{T}+nR\frac{\mathrm{d}V}{V}$

Si suponemos que la capacidad calorífica es independiente de la temperatura, la integración es inmediata

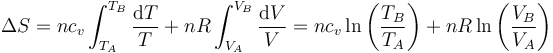
$\Delta S = nc_v\int_{T_A}^{T_B}\frac{\mathrm{d}T}{T}+nR\int_{V_A}^{V_B}\frac{\mathrm{d}V}{V}=nc_v\ln\left(\frac{T_B}{T_A}\right)+nR\ln\left(\frac{V_B}{V_A}\right)$

A partir de aquí pueden obtenerse las expresiones alternativas.

5.7 Entropía absoluta

Para dar un valor a la entropía (y no solo a su incremento), se toma un estado de referencia (las “condiciones normales”) caracterizado por una temperatura y una presión fijadas. En ese caso, la entropía de cualquier otro estado es

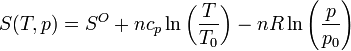
$S(T,p) = S^O + nc_p\ln\left(\frac{T}{T_0}\right)-nR\ln\left(\frac{p}{p_0}\right)$

5.8 Procesos adiabáticos reversibles

En la expresión del incremento de entropía en función de la presión y el volumen

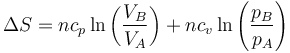
$\Delta S= nc_p\ln\left(\frac{V_B}{V_A}\right)+nc_v\ln\left(\frac{p_B}{p_A}\right)$

dividimos por $n c v$

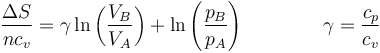
$\frac{\Delta S}{nc_v}= \gamma\ln\left(\frac{V_B}{V_A}\right)+\ln\left(\frac{p_B}{p_A}\right)\qquad\qquad \gamma = \frac{c_p}{c_v}$

y hallamos la exponencial

$\mathrm{e}^{\Delta S/nc_v}= \left(\frac{V_B}{V_A}\right)^\gamma\left(\frac{p_B}{p_A}\right) = \frac{p_BV_B^\gamma}{p_AV_A^\gamma}$

Vemos entonces que si tenemos un proceso en el que en todo momento la entropía es constante

$\Delta S = 0\qquad\Rightarrow \qquad p_BV_B^\gamma = p_AV_A^\gamma$

que es la ley de Poisson, correspondiente a un proceso adiabático reversible. Esto era de esperar, pues en un proceso de este tio el intercambio de calor reversible es nulo en todo instante $δ Q rev = 0$ y por tanto la variación de entropía es nula. Según esto, un proceso adiabático reversible es uno isentrópico.

6 Proceso adiabático irreversible

Aunque todos los procesos isentrópicos son adiabáticos, el recíproco no es cierto, por lo que conviene tener claros los dos conceptos:

Proceso adiabático: es aquel en que no hay intercambio de calor entre el sistema y el ambiente.
Proceso isentrópico: aquel en que la entropía del sistema es constante.

Para que un proceso adiabático sea isentrópico debe ser además reversible. En un proceso adiabático irreversible la entropía del universo aumenta, como en cualquier otro.

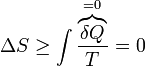
$\Delta S \geq \int \frac{\overbrace{\delta Q}^{=0}}{T} = 0$

Si tenemos la expresión general

$\mathrm{e}^{\Delta S/nc_v}= \left(\frac{V_B}{V_A}\right)^\gamma\left(\frac{p_B}{p_A}\right) = \frac{p_BV_B^\gamma}{p_AV_A^\gamma}$

y consideramos un proceso adiabático, el aumento de entropía debe ser positivo, lo que implica

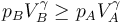
$p_BV_B^\gamma \geq p_AV_A^\gamma\,$

Para una presión final dada $p B$ esto equivale a que

$V_B\geq V_B^\mathrm{rev}\qquad\qquad T_B \geq T_B^\mathrm{rev}$

es decir, se comprime menos (o se expande más) y se calienta más (o se enfría menos) que si fuera reversible.

6.1 Experiencia de Joule

Por ejemplo, consideremos el experimento de Joule en el que un gas se encuentra contenido en una cámara adyacente a una vacía por completo. El conjunto está aislado térmicamente del exterior. Se abre la comunicación entre ambas y el gas se expande, ocupando la cámara vacía. En este proceso no se realiza trabajo, ni se absorbe calor, ni varía la energía interna. Sin embargo, es claramente irreversible (una vez que se ha expandido no puede volver a contraerse sin la intervención de un agente externo). Por tanto, la entropía debe aumentar.

La variación de la entropía la da la expresión general, teniendo en cuenta que en este caso la temperatura final es la misma que la inicial, por lo que

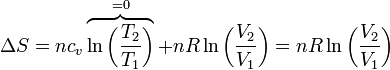
$\Delta S = nc_v\overbrace{\ln\left(\frac{T_2}{T_1}\right)}^{=0}+nR\ln\left(\frac{V_2}{V_1}\right) = nR\ln\left(\frac{V_2}{V_1}\right)$

siendo positiva ya que el volumen final es mayor que el inicial (nunca podría darse una contracción espontánea). Puesto que no hay intercambio de calor con los focos, la entropía del ambiente no cambia y ésta es toda la variación de la entropía del universo.

6.2 Compresión irreversible

Como otro ejemplo de proceso adiabático irreversible, consideremos el caso descrito en un problema en el que se tiene un cilindro adiabático cerrado por un pistón móvil en el que existe un gas en equilibrio con el exterior. Se coloca bruscamente una pesa de masa $m$ en lo alto del cilindro, comprimiendo el gas de manera irreversible. La entropía del sistema aumentará, por tanto.

La presión aumenta bruscamente al añadir la masa

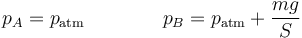
$p_A=p_\mathrm{atm}\qquad\qquad p_B = p_\mathrm{atm}+\frac{mg}{S}$

La posición final del pistón la da el que el trabajo de compresión se almacena como energía interna, por lo que

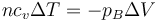
$nc_v\Delta T = -p_B\Delta V\,$

Sustituyendo la ley de los gases ideales

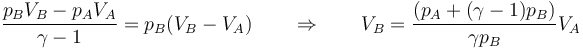
$\frac{p_BV_B-p_AV_A}{\gamma-1} = p_B(V_B-V_A)\qquad\Rightarrow\qquad V_B = \frac{(p_A +(\gamma-1) p_B)}{\gamma p_B}V_A$

y sustituyendo en la expresión para la variación en la entropia

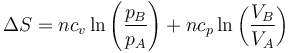
$\Delta S = nc_v\ln\left(\frac{p_B}{p_A}\right)+nc_p\ln\left(\frac{V_B}{V_A}\right)$

queda, sustituyendo

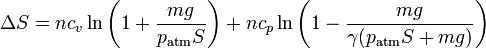
$\Delta S = nc_v\ln\left(1+\frac{mg}{p_\mathrm{atm}S}\right)+nc_p\ln\left(1-\frac{mg}{\gamma(p_\mathrm{atm}S+mg)}\right)$

7 Mezcla de gases

Supongamos que tenemos $n k$ moles de N gases, todos a la misma temperatura $T 0$ y presión $p 0$ , separados por tabiques. Si se retiran los tabiques y los gases se mezclan, se producirá un aumento de entropía, por tratarse de un proceso irreversible.

Si suponemos que los gases son ideales e inertes (esto es, que no reaccionan ni se ven afectados por el hecho de mezclarse), la entropía será la suma de las entropías individuales, como corresponde a una propiedad extensiva

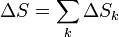
$\Delta S = \sum_k \Delta S_k\,$

A su vez, los incrementos de la entropía para cada gas serán

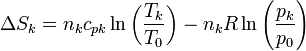
$\Delta S_k = n_k c_{pk}\ln\left(\frac{T_k}{T_0}\right)-n_kR\ln\left(\frac{p_{k}}{p_{0}}\right)$

Al mezclarse los gases la temperatura de cada gas es la misma antes y después de la mezcla. En cuanto a la presión, la presión final de la mezcla es la misma que la de cada gas al principio. Sin embargo, la presión final de cada gas no es la misma, sino que se reduce a la presión parcial

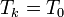
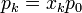
$T_k = T_0\,$ $p_k = x_kp_0\,$

ya que, por ser inertes, la variación de la entropía se calcula como si el resto de los gases no estuviera presente. Por tanto, para cada gas, es como si pasara de ocupar un espacio pequeño a uno más grande. Aquí $x k$ es la fracción molar

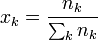
$x_k = \frac{n_k}{\sum_k n_k}$

Por tanto, la variación de la entropía para cada gas es

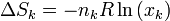
$\Delta S_k = -n_kR\ln\left(x_k\right)$

y la variación total

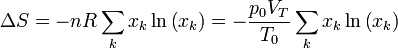
$\Delta S = -n R \sum_kx_k\ln\left(x_k\right)=-\frac{p_0V_T}{T_0}\sum_k x_k\ln\left(x_k\right)$

Esta variación es positiva, como corresponde a un proceso irreversible.

Supongamos, por ejemplo que la mezcla es de oxígeno y nitrógeno, ambos en la misma cantidad

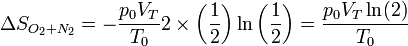
$\Delta S_{O_2+N_2} = -\frac{p_0V_T}{T_0}2\times\left(\frac{1}{2}\right)\ln\left(\frac{1}{2}\right)=\frac{p_0V_T\ln(2)}{T_0}$

El resultado anterior es independiente de qué gases sean los que se mezclan, pero, ¿qué ocurre si mezclamos oxígeno con más oxígeno? La fórmula seguiría siendo la misma. Sin embargo, si se tienen dos volúmenes del mismo gas a la misma presión y temperatura y se elimina la separación entre ellos, la situación antes de la mezcla y después, es exactamente la misma y por tanto el aumento de entropía es nulo. Hay aquí una discontinuidad que parece depender de que uno sepa qué está mezclando. Esta es la conocida como paradoja de Gibbs y su solución no es trivial.

8 Reacciones químicas

Cuando se analiza una reacción química lo que se suele hacer es

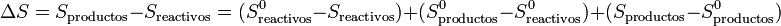
$\Delta S = S_\mathrm{productos}-S_\mathrm{reactivos}= (S^0_\mathrm{reactivos}-S_\mathrm{reactivos})+(S_\mathrm{productos}^0-S_\mathrm{reactivos}^0)+(S_\mathrm{productos}-S_\mathrm{productos}^0)$

siendo $S 0$ las entropías medidas y tabuladas en el estado estándar (normalmente a 100 kPa y 298 K). La segunda diferencia representa la variación de la entropía en la reacción en el estado estándar

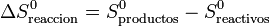
$\Delta S^0_\mathrm{reaccion}=S_\mathrm{productos}^0-S_\mathrm{reactivos}^0$

Lo que quiere decir esta descomposición en tres sumas es que, para estudiar una reacción a una cierta presión y temperatura, aprovechamos el que la entropía es una función de estado. En lugar de calcular la diferencia directamente a dicha $p$ y $T$ , lo que hacemos es imaginarnos que llevamos los reactivos, sin reaccionar, al estado estándar. Luego analizamos la reacción en el estado estándar, aprovechando los valores tabulados. Por último llevamos los productos a las condiciones originales.