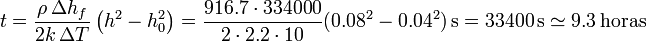Congelamiento gradual de un estanque
De Laplace
(→Solución) |
(→Solución) |
||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 15: | Línea 15: | ||
<center><math>\mathrm{d}m = \rho\,A\,\mathrm{d}h</math></center> | <center><math>\mathrm{d}m = \rho\,A\,\mathrm{d}h</math></center> | ||
| - | siendo <math>\mathrm{d}h</math> el espesor que se congela en un tiempo <math>\mathrm{d}t</math>. | + | siendo <math>\mathrm{d}h</math> el espesor que se congela en un tiempo <math>\mathrm{d}t</math> y <math>\rho</math> la densidad del ''hielo'' (916.7 kg/m³). |
La cantidad de calor que escapa del agua la da la ecuación para la conducción del calor | La cantidad de calor que escapa del agua la da la ecuación para la conducción del calor | ||
| Línea 27: | Línea 27: | ||
Podemos separar los diferenciales y escribir | Podemos separar los diferenciales y escribir | ||
| - | <center><math>h\,\mathrm{d}h = \frac{ | + | <center><math>h\,\mathrm{d}h = \frac{k\,\Delta T}{\rho\,\Delta h_f}\,\mathrm{d}t</math></center> |
Sumando todos los crecimientos diferenciales obtenemos como varía el espesor con el tiempo | Sumando todos los crecimientos diferenciales obtenemos como varía el espesor con el tiempo | ||
| - | <center><math>\int_{h_0}^h h\,\mathrm{d}h = \frac{ | + | <center><math>\int_{h_0}^h h\,\mathrm{d}h = \frac{k\,\Delta T}{\rho\,\Delta h_f}\int_0^t \mathrm{d}t</math></center> |
y nos da una ley cuadrática | y nos da una ley cuadrática | ||
| - | <center><math>\frac{h^2}{2}-\frac{h_0^2}{2} = \frac{ | + | <center><math>\frac{h^2}{2}-\frac{h_0^2}{2} = \frac{k\,\Delta T}{\rho\,\Delta h_f} t\qquad\Rightarrow\qquad h(t) = \sqrt{h_0^2+\frac{2k\,\Delta T}{\rho\,\Delta h_f} t}</math></center> |
| + | Si lo que deseamos es el tiempo entre un espesor de 4 cm y 8 cm, obtenemos | ||
| + | |||
| + | <center><math>t = \frac{\rho\,\Delta h_f}{2k\,\Delta T}\left(h^2-h_0^2\right)=\frac{916.7\cdot 334000}{2\cdot 2.2\cdot 10}(0.08^2-0.04^2)\,\mathrm{s} = 33400\,\mathrm{s} \simeq 9.3\,\mathrm{horas}</math></center> | ||
última version al 15:54 4 mar 2013
1 Enunciado
Un estanque de agua a 0 °C está cubierto por una capa de hielo de 4.00 cm de espesor. Si la temperatura del aire permanece constante a -10.0 °C, ¿cuánto tardará el espesor de la capa de hielo en alcanzar los 8.00 cm?
La conductividad térmica del hielo es 2.22 W/m·K y la entalpía de fusión del agua vale 334 kJ/kg.
2 Solución
El proceso físico en este problema es el siguiente: entre el agua del estanque y el aire exterior (que está por debajo de la temperatura de congelación del agua) existe una diferencia de temperaturas ΔT. Este gradiente produce un flujo de calor hacia el exterior. Este calor extraído del estanque se manifiesta en una congelación gradual del agua, engrosando la capa de hielo superficial.
La ecuación básica es entonces que el el calor que sale del agua en cada segundo es igual al calor necesario para que se congele una determinada cantidad de agua
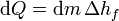
Si consideramos una porción de agua correspondiente a un área A de la superficie, la cantidad de masa congelada será
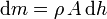
siendo dh el espesor que se congela en un tiempo dt y ρ la densidad del hielo (916.7 kg/m³).
La cantidad de calor que escapa del agua la da la ecuación para la conducción del calor
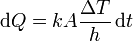
siendo k la conductividad térmica y h el espesor total de la capa de hielo. Igualando las dos cantidades queda
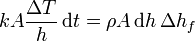
Podemos separar los diferenciales y escribir
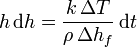
Sumando todos los crecimientos diferenciales obtenemos como varía el espesor con el tiempo
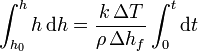
y nos da una ley cuadrática
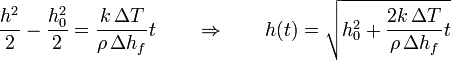
Si lo que deseamos es el tiempo entre un espesor de 4 cm y 8 cm, obtenemos