Deslizamiento de una barra
De Laplace
(Página creada con '==Enunciado== Una barra metálica de 1.00 m de longitud resbala apoyada en el suelo y en una pared vertical. En un momento dado su extremo inferior se encuentra a una dis…') |
(→Posición del CIR) |
||
| (15 ediciones intermedias no se muestran.) | |||
| Línea 4: | Línea 4: | ||
# ¿Con qué velocidad se mueve el extremo superior de la barra? | # ¿Con qué velocidad se mueve el extremo superior de la barra? | ||
| - | # Considerando un sistema de ejes centrado en la esquina, con el suelo como eje OX y la pared como eje | + | # Considerando un sistema de ejes centrado en la esquina, con el suelo como eje OX y la pared como eje OY, ¿dónde se encuentra el C.I.R. de la barra en el instante anteriormente descrito? |
==Velocidad del extremo== | ==Velocidad del extremo== | ||
| + | Existen numerosas maneras de determinar la velocidad del extremo superior. | ||
| + | |||
| + | En primer lugar determinamos la posición de este extremo. Siguiendo la sugerencia del enunciado, consideramos un sistema de ejes centrado en la esquina, con el eje OX en el suelo y el OY en la pared. En este caso, la posición del extremo inferior es | ||
| + | |||
| + | <center><math>\vec{r}_A = b\vec{\imath}=(60\vec{\imath})\,\mathrm{cm}</math></center> | ||
| + | |||
| + | y la del extremo superior es de la forma | ||
| + | |||
| + | <center><math>\vec{r}_B = h\vec{\jmath}</math></center> | ||
| + | |||
| + | Hallamos el valor de <math>h</math> por el teorema de Pitágoras | ||
| + | |||
| + | <center><math>b^2 +h^2 = L^2\qquad\Rightarrow\qquad h = \sqrt{L^2-b^2} = 80\,\mathrm{cm}</math></center> | ||
| + | |||
| + | Las velocidades de estos dos puntos son tangentes a las respectivas superficies de contacto | ||
| + | |||
| + | <center><math>\vec{v}_A = v_A\vec{\imath} = (12\vec{\imath})\frac{\mathrm{cm}}{\mathrm{s}}\qquad\qquad \vec{v}_B = v_B\vec{\jmath}</math></center> | ||
| + | |||
| + | Siendo <math>v_B</math> la cantidad que deseamos determinar. De entrada podemos decir que va a resultar una cantidad negativa, pues si el extremo inferior se aleja de la esquina, el otro debe acercarse a ella. Si no, la barra se estaría estirando. Sin embargo, no hace falta suponerlo, sino que resultará solo. | ||
| + | |||
| + | ===Por la condición de rigidez=== | ||
| + | La forma más sencilla de hallar la velocidad del extremo superior es aplicando la condición cinemática de rigidez, ya que la barra constituye un sólido rígido. Esto se expresa matemáticamente como las velocidades son equiproyectivas | ||
| + | |||
| + | <center><math>\vec{v}_B\cdot(\vec{r}_B-\vec{r}_A) = \vec{v}_A\cdot(\vec{r}_B-\vec{r}_A)</math></center> | ||
| + | |||
| + | Sustituyendo los datos conocidos | ||
| + | |||
| + | <center><math>(v_B\vec{\jmath})\cdot(h\vec{\jmath}-b\vec{\imath}) = (v_A\vec{\imath})\cdot(h\vec{k}-b\vec{\imath})\qquad\Rightarrow\qquad v_Bh = -v_A b\qquad \Rightarrow\qquad v_B = -\frac{v_Ab}{h}</math></center> | ||
| + | |||
| + | con el valor numérico, midiendo las distancias en centímetros y el tiempo en segundos, | ||
| + | |||
| + | <center><math>(v_B\vec{\jmath})\cdot(80\vec{\jmath}-60\vec{\imath}) = (12\vec{\imath})\cdot(80\vec{\jmath}-60\vec{\imath})\qquad\Rightarrow\qquad 80v_B = -720\qquad \Rightarrow\qquad v_B = -\frac{720}{80}=-9\,\frac{\mathrm{cm}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | En forma vectorial | ||
| + | <center><math> | ||
| + | \vec{v}_B =\left( -9\vec{\jmath}\right)\frac{\mathrm{cm}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | ===Empleando el teorema de Chasles=== | ||
| + | Podemos hallar la velocidad de B empleando la expresión general del campo de velocidades | ||
| + | |||
| + | <center><math>\vec{v}_B = \vec{v}_A+\vec{\omega}\times\overrightarrow{AB}</math></center> | ||
| + | |||
| + | donde, por tratarse de un movimiento plano, tenemos | ||
| + | |||
| + | <center><math>\vec{v}_A=12\vec{\imath}\qquad \qquad\overrightarrow{AB}=\vec{r}_B-\vec{r}_A=-60\vec{\imath}+80\vec{\jmath}\qquad\qquad \vec{\omega}=\omega\vec{k}\qquad\qquad \vec{v}_B=v_B\vec{\jmath}</math></center> | ||
| + | |||
| + | Sustituyendo nos queda | ||
| + | |||
| + | <center><math>v_B\vec{\jmath}=12\vec{\imath}+(\omega\vec{k})\times(-60\vec{\imath}+80\vec{\jmath})=(12-80\omega)\vec{\imath}-60\omega\vec{\jmath}</math></center> | ||
| + | |||
| + | Igualamos componente a componente | ||
| + | |||
| + | <center><math>0 = 12-80\omega\qquad\qquad v_B = -60\omega</math></center> | ||
| + | |||
| + | y obtenemos simultáneamente el valor de la velocidad angular de la barra y la del extremo B | ||
| + | |||
| + | <center><math>\omega = \frac{12}{80}\,\mathrm{s}^{-1}=0.15\,\mathrm{s}^{-1}\qquad\qquad v_B = -\frac{60\cdot 12}{80}\,\frac{\mathrm{cm}}{\mathrm{s}} = -9\,\frac{\mathrm{cm}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | ===A partir del CIR=== | ||
| + | [[Archivo:velocidad-barra-desliza.png|right]] | ||
| + | |||
| + | Otra posibilidad para hallar la velocidad del extremo superior es con ayuda del centro instantáneo de rotación. Un sólido rígido en un movimiento plano efectúa en cada instante un movimiento de rotación en torno a su CIR. La rapidez de cada punto es proporcional a la distancia al CIR, por lo que | ||
| + | |||
| + | <center><math>\left|\vec{v}_1\right| = |\vec{\omega}|d_1\qquad\qquad \left|\vec{v}_2\right| = |\vec{\omega}|d_2</math></center> | ||
| + | |||
| + | Dividiendo una por la otra eliminamos la velocidad angular, que desconocemos | ||
| + | |||
| + | <center><math>\frac{\left|\vec{v}_2\right|}{\left|\vec{v}_1\right|} = \frac{d_2}{d_1}\qquad\Rightarrow\qquad \left|\vec{v}_2\right|=\frac{d_2}{d_1}\left|\vec{v}_1\right|</math></center> | ||
| + | |||
| + | Tal como se ve en el apartado siguiente, el CIR se halla, para el instante del enunciado, en | ||
| + | |||
| + | <center><math>\vec{r}_I =b\vec{\imath}+h\vec{k}=\left(60\vec{\imath}+80\vec{k}\right)\mathrm{cm}</math></center> | ||
| + | |||
| + | y las distancias de lo extremos a este punto valen | ||
| + | |||
| + | <center><math>d_1 = h = 80\,\mathrm{cm}\qquad \qquad d_2 = b = 60\,\mathrm{cm}</math></center> | ||
| + | |||
| + | lo que nos da la rapidez | ||
| + | |||
| + | <center><math>\left|\vec{v}_2\right| = \frac{60}{80}12\,\frac{\mathrm{cm}}{\mathrm{s}}=9\,\frac{\mathrm{cm}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | La dirección de movimiento es tangente a la pared y en sentido hacia abajo, con lo que queda la velocidad | ||
| + | |||
| + | <center><math> | ||
| + | \vec{v}_2 =\left( -9\vec{k}\right)\frac{\mathrm{cm}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | ===Derivando respecto al tiempo=== | ||
| + | Una tercera forma consiste en derivar la posición del extremo superior respecto al tiempo. Sabemos que la longitud de la barra es constante en todo momento, por lo que esta posición se puede escribir | ||
| + | |||
| + | <center><math>h(t)^2+b(t)^2 = L^2\qquad\Rightarrow\qquad h(t) = \sqrt{L^2-b(t)^2}\qquad\qquad \vec{r}_2 = \sqrt{L^2-b(t)^2}\vec{k}</math></center> | ||
| + | |||
| + | Derivando aquí respecto al tiempo | ||
| + | |||
| + | <center><math>\vec{v}_2 = \frac{\mathrm{d}\vec{r}_2}{\mathrm{d}t}=\dot{h}\vec{k}=-\frac{b\dot{b}}{\sqrt{L^2-b^2}}\vec{k}=-\frac{b\dot{b}}{h}\vec{k}</math></center> | ||
| + | |||
| + | Sustituyendo los datos obtenemos el resultado ya conocido | ||
| + | |||
| + | <center><math>\vec{v}_2 = -\frac{60\cdot 12}{80}\vec{k}\,\frac{\mathrm{cm}}{\mathrm{s}} =\left( -9\vec{k}\right)\frac{\mathrm{cm}}{\mathrm{s}}</math></center> | ||
| + | |||
==Posición del CIR== | ==Posición del CIR== | ||
| + | La forma más sencilla de determinar la posición del centro instantáneo de rotación es mediante un método gráfico. El CIR se encuentra trazando la perpendicular por un punto a la velocidad de dicho punto, para dos puntos diferentes, y localizando la intersección de estas dos rectas. | ||
| + | |||
| + | Para el punto <math>\vec{r}_1</math> la perpendicular es la recta vertical que pasa por este punto. La ecuación de esta recta es simplemente | ||
| + | |||
| + | <center><math>x = b = 60\,\mathrm{cm}</math></center> | ||
| + | |||
| + | Para el punto <math>\vec{r}_2</math> se trata de la recta horizontal situada a la altura de este extremo | ||
| + | |||
| + | <center><math>y = h = 80\,\mathrm{cm}</math></center> | ||
| + | |||
| + | El CIR se encuentra en la intersección de estas dos rectas, esto es, es el punto | ||
| + | |||
| + | <center><math>x = b = 60\,\mathrm{cm}\qquad\qquad y = h = 80\,\mathrm{cm}</math></center> | ||
| + | |||
| + | o, en forma vectorial | ||
| + | |||
| + | <center><math>\vec{r}_I = b\vec{\imath}+h\vec{\jmath} = \left(60\vec{\imath}+80\vec{\jmath}\right)\,\mathrm{cm}</math></center> | ||
| + | |||
[[Categoría:Problemas de cinemática del sólido rígido (GIE)]] | [[Categoría:Problemas de cinemática del sólido rígido (GIE)]] | ||
| + | [[Categoría:Problemas de cinemática del sólido rígido]] | ||
última version al 10:45 24 sep 2015
Contenido |
1 Enunciado
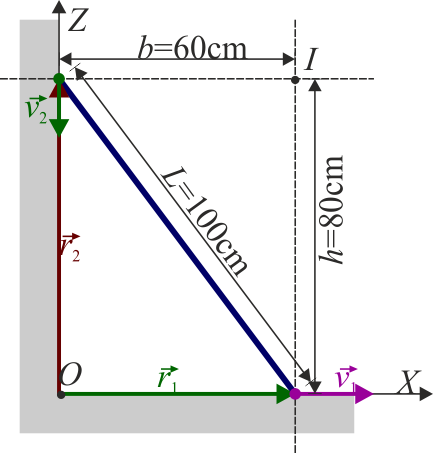
Una barra metálica de 1.00 m de longitud resbala apoyada en el suelo y en una pared vertical. En un momento dado su extremo inferior se encuentra a una distancia de 60 cm de la esquina y se mueve con velocidad de 12 cm/s alejándose de la esquina
- ¿Con qué velocidad se mueve el extremo superior de la barra?
- Considerando un sistema de ejes centrado en la esquina, con el suelo como eje OX y la pared como eje OY, ¿dónde se encuentra el C.I.R. de la barra en el instante anteriormente descrito?
2 Velocidad del extremo
Existen numerosas maneras de determinar la velocidad del extremo superior.
En primer lugar determinamos la posición de este extremo. Siguiendo la sugerencia del enunciado, consideramos un sistema de ejes centrado en la esquina, con el eje OX en el suelo y el OY en la pared. En este caso, la posición del extremo inferior es
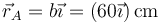
y la del extremo superior es de la forma
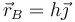
Hallamos el valor de h por el teorema de Pitágoras

Las velocidades de estos dos puntos son tangentes a las respectivas superficies de contacto
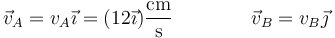
Siendo vB la cantidad que deseamos determinar. De entrada podemos decir que va a resultar una cantidad negativa, pues si el extremo inferior se aleja de la esquina, el otro debe acercarse a ella. Si no, la barra se estaría estirando. Sin embargo, no hace falta suponerlo, sino que resultará solo.
2.1 Por la condición de rigidez
La forma más sencilla de hallar la velocidad del extremo superior es aplicando la condición cinemática de rigidez, ya que la barra constituye un sólido rígido. Esto se expresa matemáticamente como las velocidades son equiproyectivas
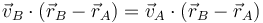
Sustituyendo los datos conocidos
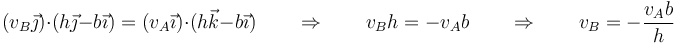
con el valor numérico, midiendo las distancias en centímetros y el tiempo en segundos,

En forma vectorial
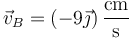
2.2 Empleando el teorema de Chasles
Podemos hallar la velocidad de B empleando la expresión general del campo de velocidades
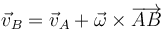
donde, por tratarse de un movimiento plano, tenemos
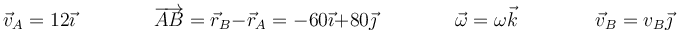
Sustituyendo nos queda
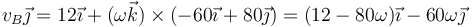
Igualamos componente a componente

y obtenemos simultáneamente el valor de la velocidad angular de la barra y la del extremo B
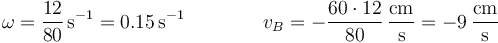
2.3 A partir del CIR
Otra posibilidad para hallar la velocidad del extremo superior es con ayuda del centro instantáneo de rotación. Un sólido rígido en un movimiento plano efectúa en cada instante un movimiento de rotación en torno a su CIR. La rapidez de cada punto es proporcional a la distancia al CIR, por lo que

Dividiendo una por la otra eliminamos la velocidad angular, que desconocemos
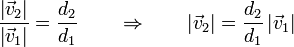
Tal como se ve en el apartado siguiente, el CIR se halla, para el instante del enunciado, en
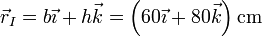
y las distancias de lo extremos a este punto valen

lo que nos da la rapidez
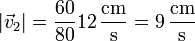
La dirección de movimiento es tangente a la pared y en sentido hacia abajo, con lo que queda la velocidad
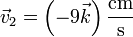
2.4 Derivando respecto al tiempo
Una tercera forma consiste en derivar la posición del extremo superior respecto al tiempo. Sabemos que la longitud de la barra es constante en todo momento, por lo que esta posición se puede escribir
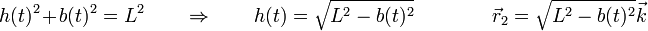
Derivando aquí respecto al tiempo
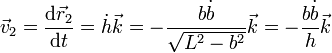
Sustituyendo los datos obtenemos el resultado ya conocido
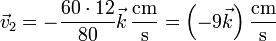
3 Posición del CIR
La forma más sencilla de determinar la posición del centro instantáneo de rotación es mediante un método gráfico. El CIR se encuentra trazando la perpendicular por un punto a la velocidad de dicho punto, para dos puntos diferentes, y localizando la intersección de estas dos rectas.
Para el punto 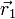 la perpendicular es la recta vertical que pasa por este punto. La ecuación de esta recta es simplemente
la perpendicular es la recta vertical que pasa por este punto. La ecuación de esta recta es simplemente
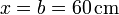
Para el punto 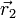 se trata de la recta horizontal situada a la altura de este extremo
se trata de la recta horizontal situada a la altura de este extremo
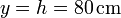
El CIR se encuentra en la intersección de estas dos rectas, esto es, es el punto

o, en forma vectorial