Entrar Página Discusión Historial Go to the site toolbox

Rodadura por una pendiente

De Laplace

(Diferencias entre revisiones)
(→Solución)
 
(10 ediciones intermedias no se muestran.)
Línea 1: Línea 1:
==Enunciado==
==Enunciado==
-
En lo alto de un plano inclinado de altura 1.2 m y con una pendiente del 75% se encuentran los siguientes objetos, todos ellos de masa 0.5 kg y radio 10 cm:
+
En lo alto de un plano inclinado de altura <math>h</math> y con una cierta pendiente se encuentran los siguientes objetos
* Una superficie cilíndrica hueca
* Una superficie cilíndrica hueca
Línea 7: Línea 7:
* Una esfera maciza
* Una esfera maciza
-
Si se sueltan a la vez desde el extremo superior del plano, ¿con qué velocidad llega cada uno al punto más bajo del plano? ¿en qué orden llegarán y cuanto tarda cada uno en llegar? Si además se suelta un bloque de 0.5&thinsp;kg que desliza sin rozamiento por el plano, ¿llegará antes o después que los objetos rodantes? ¿Cuánto?
+
Si se sueltan a la vez desde el extremo superior del plano, ¿dependerá el orden de llegada de la masa y el radio de cada uno? ¿con qué rapidez del CM llega cada uno al punto más bajo del plano? ¿en qué orden llegarán y cuanto tarda cada uno en llegar? Si además se suelta un bloque que desliza sin rozamiento por el plano, ¿llegará antes o después que los objetos rodantes? ¿Cuánto?
==Solución==
==Solución==
Línea 23: Línea 23:
Esta ecuación se interpreta como que la energía potencial se va en parte en energía cinética de traslación y en energía cinética de rotación. Puesto que lo que determina cuál llega en menos tiempo al punto más bajo es la velocidad del CM, se deduce que el ganador de la competición será el que tenga menos energía cinética de rotación. Esto dependerá esencialmente de su momento de inercia.
Esta ecuación se interpreta como que la energía potencial se va en parte en energía cinética de traslación y en energía cinética de rotación. Puesto que lo que determina cuál llega en menos tiempo al punto más bajo es la velocidad del CM, se deduce que el ganador de la competición será el que tenga menos energía cinética de rotación. Esto dependerá esencialmente de su momento de inercia.
-
 
-
La velocidad angular con la que rueda cada uno nos la da el que el CIR se encuentra en el punto de contacto del cuerpo con el suelo y por tanto el CM de cada uno se encuentra describiendo un movimiento de rotación en torno a este punto, situado a una distancia R. Por tanto, la velocidad del CM cumple, en cada caso
 
-
 
-
<center><math>|\vec{v}_C| = |\vec{\omega}|R</math></center>
 
-
 
-
lo que, llevado a la ley de conservación de la energía mecánica, nos da
 
-
 
-
<center><math>\frac{1}{2}\left(m+\frac{I}{R^2}\right)|\vec{v}_C|^2 = mgH</math></center>
 
Para los cuatro cuerpos en cuestión, el momento de inercia respecto a un eje que pasa por el CM es de la forma
Para los cuatro cuerpos en cuestión, el momento de inercia respecto a un eje que pasa por el CM es de la forma
Línea 51: Línea 43:
| <math>\frac{2}{3}</math>
| <math>\frac{2}{3}</math>
| <math>\frac{2}{5}</math>
| <math>\frac{2}{5}</math>
 +
|}
 +
 +
La velocidad angular con la que rueda cada uno nos la da el que el CIR se encuentra en el punto de contacto del cuerpo con el suelo y por tanto el CM de cada uno se encuentra describiendo un movimiento de rotación en torno a este punto, situado a una distancia R. Por tanto, la velocidad del CM cumple, en cada caso
 +
 +
<center><math>|\vec{v}_C| = |\vec{\omega}|R</math></center>
 +
 +
lo que, llevado a la ley de conservación de la energía mecánica, nos da
 +
 +
<center><math>\frac{1}{2}\left(1+\gamma\right)|\vec{v}_C|^2 = gH</math></center>
 +
 +
y esto nos da la velocidad de llegada
 +
 +
<center><math>|\vec{v}_C|=\sqrt{\frac{2gH}{1+\gamma}}</math></center>
 +
 +
Vemos que el resultado es independiente de la masa y del radio del cuerpo (y de la pendiente del plano). Lo único que necesitamos conocer es la altura del plano y la forma del objeto. Cuanto mayor sea el factor <math>\gamma</math> más lento llega el cuerpo. dado que se cumple
 +
 +
<center><math>\frac{2}{5} <\frac{1}{2} < \frac{2}{3} < 1</math></center>
 +
 +
El orden de llegada será
 +
 +
# Esfera maciza
 +
# Cilindro macizo
 +
# Esfera hueca
 +
# Cilindro hueco
 +
 +
Antes que todos ellos llegaría un bloque que deslizara sin fricción por el plano, ya que para este cuerpo toda la energía potencial se convierte en energía cinética de traslación. Matemáticamente, esto equivale a <math>\gamma = 0</math>
 +
 +
En cuanto al tiempo que tarda cada uno llegar, el CM de cada uno de los cuerpos sigue un movimiento uniformemente acelerado con velocidad inicial nula y final la que acabamos de calcular. En su movimiento recorre una distancia
 +
 +
<center><math>L = \frac{H}{\mathrm{sen}(\theta)}</math></center>
 +
 +
Las ecuaciones para el movimiento uniformemente acelerado nos dan, para el intervalo completo
 +
 +
<center><math>L = \frac{1}{2}a T^2\qquad\qquad |\vec{v}_C| = a T</math></center>
 +
 +
Eliminamos la aceleración (que no conocemos aun, ya que será diferente para cada uno de los cuerpos) dividiendo y obtenemos
 +
 +
<center><math>T = \frac{2L}{|\vec{v}_C|}=\sqrt{1+\gamma}\frac{2L}{\sqrt{2gH}}=\sqrt{1+\gamma}\sqrt{\frac{2H}{g}}\frac{1}{\mathrm{sen}(\theta)}</math></center>
 +
 +
Si llamamos
 +
 +
<center><math>v_D = \sqrt{2gH}\qquad\qquad T_D =\sqrt{\frac{2H}{g}}\frac{1}{\mathrm{sen}(\theta)}</math></center>
 +
 +
la velocidad que tendría y el tiempo que emplearía un bloque deslizante, se cumple, para cada cuerpo
 +
 +
{| class="bordeado"
 +
|-
 +
! Cuerpo
 +
! <math>\gamma</math>
 +
! <math>|\vec{v}_C|/v_D</math>
 +
! <math>T/T_D\,</math>
 +
! <math>|T-T_D|/T_D\,</math> (%)
 +
|-
 +
| Bloque
 +
| 0
 +
| 1
 +
| 1
 +
| 0
 +
|-
 +
| Esfera maciza
 +
| 2/5
 +
| 0.845
 +
| 1.183
 +
| 18.3
 +
|-
 +
| Cilindro macizo
 +
| 1/2
 +
| 0.816
 +
| 1.225
 +
| 22.5
 +
|-
 +
| Esfera hueca
 +
| 2/3
 +
| 0.775
 +
| 1.291
 +
| 29.1
 +
|-
 +
| Cilindro hueco
 +
| 1
 +
| 0.707
 +
| 1.414
 +
| 41.4
|}
|}
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]]
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]]

última version al 12:50 9 ene 2013

1 Enunciado

En lo alto de un plano inclinado de altura h y con una cierta pendiente se encuentran los siguientes objetos

  • Una superficie cilíndrica hueca
  • Un cilindro macizo
  • Una superficie esférica hueca
  • Una esfera maciza

Si se sueltan a la vez desde el extremo superior del plano, ¿dependerá el orden de llegada de la masa y el radio de cada uno? ¿con qué rapidez del CM llega cada uno al punto más bajo del plano? ¿en qué orden llegarán y cuanto tarda cada uno en llegar? Si además se suelta un bloque que desliza sin rozamiento por el plano, ¿llegará antes o después que los objetos rodantes? ¿Cuánto?

2 Solución

Este problema se resuelve de forma sencilla aplicando la ley de conservación de la energía mecánica. Cuando se encuentran en reposo en el punto más alto del plano, cada uno de los cuerpos posee una energía mecánica igual a su energía potencial, medida desde el punto más bajo del plano, de

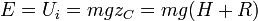
E=U_i = mgz_C = mg(H+R)\,

Al descender por el plano, parte de esta energía potencial se transforma en energía cinética. Por tratarse de cuatro sólidos con simetría de revolución, la energía mecánica final puede escribirse

E=\frac{1}{2}m|\vec{v}_C|^2 + \frac{1}{2}I|\vec{\omega}|^2 + mgR

Puesto que la energía mecánica se conserva, estas dos cantidades deben ser iguales y por tanto

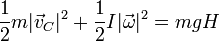
\frac{1}{2}m|\vec{v}_C|^2 + \frac{1}{2}I|\vec{\omega}|^2 = mgH

Esta ecuación se interpreta como que la energía potencial se va en parte en energía cinética de traslación y en energía cinética de rotación. Puesto que lo que determina cuál llega en menos tiempo al punto más bajo es la velocidad del CM, se deduce que el ganador de la competición será el que tenga menos energía cinética de rotación. Esto dependerá esencialmente de su momento de inercia.

Para los cuatro cuerpos en cuestión, el momento de inercia respecto a un eje que pasa por el CM es de la forma

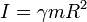
I = \gamma m R^2\,

donde γ vale

Cuerpo Cilindro hueco Cilindro macizo Esfera hueca Esfera maciza
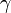
\gamma\, 1\, \frac{1}{2} \frac{2}{3} \frac{2}{5}

La velocidad angular con la que rueda cada uno nos la da el que el CIR se encuentra en el punto de contacto del cuerpo con el suelo y por tanto el CM de cada uno se encuentra describiendo un movimiento de rotación en torno a este punto, situado a una distancia R. Por tanto, la velocidad del CM cumple, en cada caso

|\vec{v}_C| = |\vec{\omega}|R

lo que, llevado a la ley de conservación de la energía mecánica, nos da

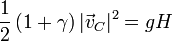
\frac{1}{2}\left(1+\gamma\right)|\vec{v}_C|^2 = gH

y esto nos da la velocidad de llegada

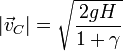
|\vec{v}_C|=\sqrt{\frac{2gH}{1+\gamma}}

Vemos que el resultado es independiente de la masa y del radio del cuerpo (y de la pendiente del plano). Lo único que necesitamos conocer es la altura del plano y la forma del objeto. Cuanto mayor sea el factor γ más lento llega el cuerpo. dado que se cumple

\frac{2}{5} <\frac{1}{2} < \frac{2}{3} < 1

El orden de llegada será

  1. Esfera maciza
  2. Cilindro macizo
  3. Esfera hueca
  4. Cilindro hueco

Antes que todos ellos llegaría un bloque que deslizara sin fricción por el plano, ya que para este cuerpo toda la energía potencial se convierte en energía cinética de traslación. Matemáticamente, esto equivale a γ = 0

En cuanto al tiempo que tarda cada uno llegar, el CM de cada uno de los cuerpos sigue un movimiento uniformemente acelerado con velocidad inicial nula y final la que acabamos de calcular. En su movimiento recorre una distancia

L = \frac{H}{\mathrm{sen}(\theta)}

Las ecuaciones para el movimiento uniformemente acelerado nos dan, para el intervalo completo

L = \frac{1}{2}a T^2\qquad\qquad |\vec{v}_C| = a T

Eliminamos la aceleración (que no conocemos aun, ya que será diferente para cada uno de los cuerpos) dividiendo y obtenemos

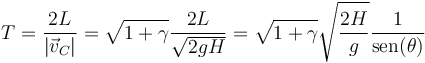
T = \frac{2L}{|\vec{v}_C|}=\sqrt{1+\gamma}\frac{2L}{\sqrt{2gH}}=\sqrt{1+\gamma}\sqrt{\frac{2H}{g}}\frac{1}{\mathrm{sen}(\theta)}

Si llamamos

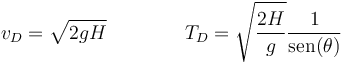
v_D = \sqrt{2gH}\qquad\qquad T_D =\sqrt{\frac{2H}{g}}\frac{1}{\mathrm{sen}(\theta)}

la velocidad que tendría y el tiempo que emplearía un bloque deslizante, se cumple, para cada cuerpo

Cuerpo γ |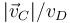\vec{v}_C|/v_D T/T_D\, |T-T_D|/T_D\, (%)
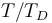
Bloque 0 1 1 0
Esfera maciza 2/5 0.845 1.183 18.3
Cilindro macizo 1/2 0.816 1.225 22.5
Esfera hueca 2/3 0.775 1.291 29.1
Cilindro hueco 1 0.707 1.414 41.4
Obtenido de "http://tesla.us.es/wiki/index.php/Rodadura_por_una_pendiente"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 12:50, 9 ene 2013. - Esta página ha sido visitada 32.278 veces. - Aviso legal - Acerca de Laplace