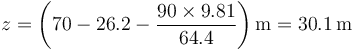Entrar Página Discusión Historial Go to the site toolbox

Energía en el salto desde un puente

De Laplace

(Diferencias entre revisiones)
(→Enunciado)
 
(4 ediciones intermedias no se muestran.)
Línea 9: Línea 9:
==Primer salto==
==Primer salto==
 +
La solución de este problema es una simple aplicación del teorema de conservación de la energía mecánica. Suponemos despreciable el rozamiento, de forma que no hay fuerzas disipativas en el sistema.
 +
 +
Inicialmente tenemos a Alberto en lo alto del puente, en reposo. Su energía cinética es nula en este momento. La energía potencial será suma de la gravitatoria más la elástica. Si tomamos el origen de alturas en el nivel del agua, la energía potencial gravitatoria será
 +
 +
<center><math>U_g = m_AgH\,</math></center>
 +
 +
siendo <math>H</math> la altura del puente y <math>m_A</math> la masa de Alberto. La energía potencial elástica es nula en este momento, ya que al tratarse de una cuerda flexible, solo produce fuerza y almacena energía cuando su longitud es mayor que la de reposo, pero no cuando es menor. Por tanto, la energía mecánica total es simplemente
 +
 +
<center><math>E = 0 + m_AgH+0 = m_AgH = (75\,\mathrm{kg})\left(9.81\,\frac{\mathrm{N}}{\mathrm{kg}}\right)\left(70\,\mathrm{m}\right) = 51500\,\mathrm{J}</math></center>
 +
 +
Cuando llega al punto más bajo, su energía cinética vuelve a ser cero, ya que llega a rozar el agua y a partir de ahí vuelve a subir, por lo que se encuentra en una posición de reposo instantáneo. La energía potencial también es nula, ya que hemos tomado el nivel del río como referencia. La energía potencial elástica no es nula, ya que ahora la cuerda está tensa. Por tanto
 +
 +
<center><math>E = \frac{1}{2}k(H-L)^2</math></center>
 +
 +
siendo <math>L</math> la longitud en reposo de la cuerda y <math>H-L</math> lo que se estira. Igualando la energía inicial con la final
 +
 +
<center><math>m_AgH = \frac{1}{2}k(H-L)^2</math></center>
 +
 +
Vemos que toda la energía potencial gravitatoria se transforma en elástica.
 +
 +
De aquí despejamos la constante del muelle
 +
 +
<center><math>k = \frac{2m_AgH}{(H-L)^2}=\frac{2\cdot 75 \cdot 9.81\cdot 70}{40^2}\,\frac{\mathrm{N}}{\mathrm{m}}=64.4\,\frac{\mathrm{N}}{\mathrm{m}}</math></center>
 +
==Segundo salto==
==Segundo salto==
 +
En el segundo salto, tenemos la misma constante elástica, pero una mayor energía potencial inicial
 +
 +
<center><math>U_g = m_B g H\,</math></center>
 +
 +
con <math>m_B</math> la masa de Benito. Esto quiere decir que cuando éste salta y llega al borde del agua, hay un exceso de energía mecánica que no se ha convertido en energía potencial elástica (que no depende de la masa), por lo que sigue habiendo energía cinética. Dicho en otras palabras, que Benito impacta con el agua.
 +
 +
Igualando la energía mecánica inicial y la final
 +
 +
<center><math>m_BgH = \frac{1}{2}k(H-L)^2+\frac{1}{2}m_B v_B^2</math></center>
 +
 +
Si restamos de esta ecuación la igualdad del apartado anterior queda
 +
 +
<center><math>(m_B-m_A)gH = \frac{1}{2}m_Bv_B^2</math></center>
 +
 +
y despejando
 +
 +
<center><math>v_B=\sqrt{\frac{2(m_B-m_A)gH}{m_B}}</math></center>
 +
 +
siendo su valor numérico
 +
 +
<center><math>v_B = 15.1\,\frac{\mathrm{m}}{\mathrm{s}} = 54.5\,\frac{\mathrm{km}}{\mathrm{h}}</math></center>
 +
 +
Si no quiere darse el golpe, deberá previamente recoger cuerda, reduciendo el valor de L. Estableciendo de nuevo la igualdad en la energía mecánica, pero imponiendo que no tenga energía cinética queda
 +
 +
<center><math>m_B gH = \frac{1}{2}k(H-L')^2 \qquad\Rightarrow\qquad L' = H - \sqrt{\frac{2m_Bg H}{k}}</math></center>
 +
 +
lo que da una longitud
 +
 +
<center><math>L' = 26.2\,\mathrm{m}\qquad\Rightarrow\qquad \Delta L = L - L' = 3.8\,\mathrm{m}</math></center>
==Posiciones de equilibrio==
==Posiciones de equilibrio==
 +
El equilibrio se da cuando se anula la suma de las fuerzas que actúan sobre la masa. En este caso, las dos fuerzas son el peso (que tira hacia abajo) y la fuerza elástica (que va hacia arriba).
 +
 +
Si acaba a una altura z, la longitud de la cuerda en ese momento es H - z y la elongación H - z - L. Por tanto, la condición de equilibrio es
 +
 +
<center><math>k(H-L-z) - m_A g = 0 \qquad\Rightarrow\qquad z = H - L - \frac{m_A g}{k}</math></center>
 +
 +
Esto da, para Alberto,
 +
 +
<center><math>z = \left(70 - 30 - \frac{75\times 9.81}{64.4}\right)\mathrm{m} = 28.6\,\mathrm{m}</math></center>
 +
 +
y para Benito
 +
 +
<center><math>z = \left(70 - 26.2 - \frac{90\times 9.81}{64.4}\right)\mathrm{m} = 30.1\,\mathrm{m}</math></center>
 +
[[Categoría:Problemas de energía y leyes de conservación (GIE)]]
[[Categoría:Problemas de energía y leyes de conservación (GIE)]]

última version al 20:28 24 ene 2015

Contenido

1 Enunciado

Haciendo puenting (bungee jumping en inglés), Alberto, de 75 kg, se deja caer desde el pretil de un puente situado a 70 m de altura sobre un río empleando una cuerda elástica de 30 m.

  1. Determine la constante elástica k que debe tener la cuerda para que Alberto llegue a rozar el agua del río.
  2. Si, empleando la misma goma, se deja caer Benito, de 90 kg, ¿con qué rapidez impactará con el agua? ¿Cuánta cuerda debería recoger si quiere llegar él también rozando al agua?
  3. Tras unas cuantas oscilaciones, Alberto queda colgando en equilibrio. ¿A qué altura sobre el nivel del agua se para? ¿Y Benito, después de haber recogido la cuerda?

2 Primer salto

La solución de este problema es una simple aplicación del teorema de conservación de la energía mecánica. Suponemos despreciable el rozamiento, de forma que no hay fuerzas disipativas en el sistema.

Inicialmente tenemos a Alberto en lo alto del puente, en reposo. Su energía cinética es nula en este momento. La energía potencial será suma de la gravitatoria más la elástica. Si tomamos el origen de alturas en el nivel del agua, la energía potencial gravitatoria será

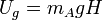
U_g = m_AgH\,

siendo H la altura del puente y mA la masa de Alberto. La energía potencial elástica es nula en este momento, ya que al tratarse de una cuerda flexible, solo produce fuerza y almacena energía cuando su longitud es mayor que la de reposo, pero no cuando es menor. Por tanto, la energía mecánica total es simplemente

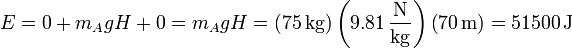
E = 0 + m_AgH+0 = m_AgH = (75\,\mathrm{kg})\left(9.81\,\frac{\mathrm{N}}{\mathrm{kg}}\right)\left(70\,\mathrm{m}\right) = 51500\,\mathrm{J}

Cuando llega al punto más bajo, su energía cinética vuelve a ser cero, ya que llega a rozar el agua y a partir de ahí vuelve a subir, por lo que se encuentra en una posición de reposo instantáneo. La energía potencial también es nula, ya que hemos tomado el nivel del río como referencia. La energía potencial elástica no es nula, ya que ahora la cuerda está tensa. Por tanto

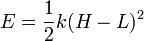
E = \frac{1}{2}k(H-L)^2

siendo L la longitud en reposo de la cuerda y H − L lo que se estira. Igualando la energía inicial con la final

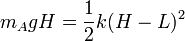
m_AgH = \frac{1}{2}k(H-L)^2

Vemos que toda la energía potencial gravitatoria se transforma en elástica.

De aquí despejamos la constante del muelle

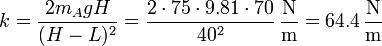
k = \frac{2m_AgH}{(H-L)^2}=\frac{2\cdot 75 \cdot 9.81\cdot 70}{40^2}\,\frac{\mathrm{N}}{\mathrm{m}}=64.4\,\frac{\mathrm{N}}{\mathrm{m}}

3 Segundo salto

En el segundo salto, tenemos la misma constante elástica, pero una mayor energía potencial inicial

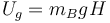
U_g = m_B g H\,

con mB la masa de Benito. Esto quiere decir que cuando éste salta y llega al borde del agua, hay un exceso de energía mecánica que no se ha convertido en energía potencial elástica (que no depende de la masa), por lo que sigue habiendo energía cinética. Dicho en otras palabras, que Benito impacta con el agua.

Igualando la energía mecánica inicial y la final

m_BgH = \frac{1}{2}k(H-L)^2+\frac{1}{2}m_B v_B^2

Si restamos de esta ecuación la igualdad del apartado anterior queda

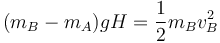
(m_B-m_A)gH = \frac{1}{2}m_Bv_B^2

y despejando

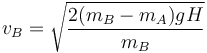
v_B=\sqrt{\frac{2(m_B-m_A)gH}{m_B}}

siendo su valor numérico

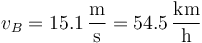
v_B = 15.1\,\frac{\mathrm{m}}{\mathrm{s}} = 54.5\,\frac{\mathrm{km}}{\mathrm{h}}

Si no quiere darse el golpe, deberá previamente recoger cuerda, reduciendo el valor de L. Estableciendo de nuevo la igualdad en la energía mecánica, pero imponiendo que no tenga energía cinética queda

m_B gH = \frac{1}{2}k(H-L')^2 \qquad\Rightarrow\qquad L' = H - \sqrt{\frac{2m_Bg H}{k}}

lo que da una longitud

L' = 26.2\,\mathrm{m}\qquad\Rightarrow\qquad \Delta L = L - L' = 3.8\,\mathrm{m}

4 Posiciones de equilibrio

El equilibrio se da cuando se anula la suma de las fuerzas que actúan sobre la masa. En este caso, las dos fuerzas son el peso (que tira hacia abajo) y la fuerza elástica (que va hacia arriba).

Si acaba a una altura z, la longitud de la cuerda en ese momento es H - z y la elongación H - z - L. Por tanto, la condición de equilibrio es

k(H-L-z) - m_A g = 0 \qquad\Rightarrow\qquad z = H - L - \frac{m_A g}{k}

Esto da, para Alberto,

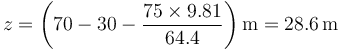
z = \left(70 - 30 - \frac{75\times 9.81}{64.4}\right)\mathrm{m} = 28.6\,\mathrm{m}

y para Benito

z = \left(70 - 26.2 - \frac{90\times 9.81}{64.4}\right)\mathrm{m} = 30.1\,\mathrm{m}
Obtenido de "http://tesla.us.es/wiki/index.php/Energ%C3%ADa_en_el_salto_desde_un_puente"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 20:28, 24 ene 2015. - Esta página ha sido visitada 21.513 veces. - Aviso legal - Acerca de Laplace