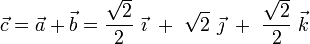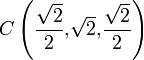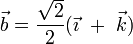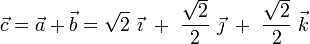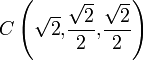Cuestión de álgebra vectorial, Noviembre 2011
De Laplace
(→Coordenadas del vértice C) |
(→Longitud de la diagonal) |
||
| (26 ediciones intermedias no se muestran.) | |||
| Línea 34: | Línea 34: | ||
<center><math>S_{OACB}= \mathrm{sen}\!\ \theta=\frac{\sqrt{3}}{2}</math>{{qquad}}{{tose}}{{qquad}}<math style="border:solid grey 2px;padding:10px">\theta=\frac{\pi}{3}</math></center> | <center><math>S_{OACB}= \mathrm{sen}\!\ \theta=\frac{\sqrt{3}}{2}</math>{{qquad}}{{tose}}{{qquad}}<math style="border:solid grey 2px;padding:10px">\theta=\frac{\pi}{3}</math></center> | ||
| - | Y con este resultado ya podemos | + | Y con este resultado ya podemos determinar la magnitud de la diagonal del rombo: |
<center><math style="border:solid purple 2px;padding:10px" | <center><math style="border:solid purple 2px;padding:10px" | ||
| Línea 48: | Línea 48: | ||
Por su parte, sabemos que el vector <math>\vec{b}</math> forma un ángulo <math>\pi/4</math> con el eje <math>OZ</math>, pero desconocemos los ángulos <math>\alpha</math> y <math>\beta</math> que forma con los ejes <math>OX</math> y <math>OY</math>; es decir, desconocemos sus componentes cartesianas “<math>x</math>” e “<math>y</math>”: | Por su parte, sabemos que el vector <math>\vec{b}</math> forma un ángulo <math>\pi/4</math> con el eje <math>OZ</math>, pero desconocemos los ángulos <math>\alpha</math> y <math>\beta</math> que forma con los ejes <math>OX</math> y <math>OY</math>; es decir, desconocemos sus componentes cartesianas “<math>x</math>” e “<math>y</math>”: | ||
| - | <center><math>\vec{b}=\cos\alpha\ \vec{\imath}\ + \cos\beta\ \vec{\jmath}\ + \cos\frac{\pi}{4}\ \vec{k}</math></center> | + | <center><math>\vec{b}=\cos\alpha\ \vec{\imath}\ + \cos\beta\ \vec{\jmath}\ + \cos\frac{\pi}{4}\ \vec{k}=b_x \ \vec{\imath}\ + b_y \ \vec{\jmath}\ + \ \frac{\sqrt{2}}{2}\ \vec{k}</math></center> |
| - | <center><math>\ | + | Para determinar los valores de las coordenadas desconocidas utilizaremos dos datos que conocemos: el módulo del vector <math>\vec{b}</math> y el valor del producto escalar de este vector por el <math>\vec{a}</math>, a partir de los que podremos plantear sendas ecuaciones algebraicas cuya solución serán las coordenadas desconocidas del vector <math>\vec{b}</math>: |
| + | |||
| + | <center><math>\left.\begin{array}{l}\displaystyle 1=|\vec{b}|^2=\vec{b}\cdot\vec{b}=b_x^2+b_y^2+\frac{1}{2}\\ \\ | ||
| + | \displaystyle |\vec{a}||\vec{b}|\cos\frac{\pi}{3}=\vec{a}\cdot\vec{b}=\frac{\sqrt{2}}{2}(b_x+b_y) | ||
| + | \end{array}\right\}\qquad\longrightarrow\qquad\left\{\begin{array}{l}\displaystyle b_x^2+b_y^2=\frac{1}{2}\\ \\ | ||
| + | \displaystyle b_x+b_y=\frac{\sqrt{2}}{2} | ||
| + | \end{array}\right. | ||
| + | </math></center> | ||
| + | |||
| + | Este sistema de ecuaciones admite dos soluciones posibles. Una de ellas es: | ||
| + | |||
| + | <center><math>b_x=0\mathrm{;}\qquad b_y=\frac{\sqrt{2}}{2}</math></center> | ||
| + | |||
| + | lo que implica que significa que el vector <math>\vec{b}</math> (y el punto <math>B</math>), está contenido en el plano <math>OYZ</math> (es decir, <math>\alpha=\pi/2</math>), formando también un ángulo <math>\beta=\pi/4</math> con el eje <math>OY</math>. La otra solución es... | ||
| + | |||
| + | <center><math>b_x=\frac{\sqrt{2}}{2}\mathrm{;}\qquad b_y=0</math></center> | ||
| + | |||
| + | Para ésta, el punto <math>B</math> y el vector <math>\vec{b}</math> están incluidos en el plano <math>OXZ</math> (<math>\beta=\pi/2</math>), y este último forma ángulos de <math>\pi/4</math> con los ejes <math>OX</math> y <math>OZ</math>. A cada una de estas soluciones le correponde una posición distinta del vértice <math>C</math>: | ||
| + | |||
| + | <center><math>\displaystyle\vec{b}=\frac{\sqrt{2}}{2}(\vec{\jmath}\ + \ \vec{k}) | ||
| + | </math>{{qquad}}{{tose}}{{qquad}}<math>\vec{c}=\vec{a}+\vec{b}=\frac{\sqrt{2}}{2}\ \vec{\imath}\ + \ \sqrt{2}\ \vec{\jmath}\ +\ \frac{\sqrt{2}}{2}\ \vec{k}</math>{{qquad}}{{tose}}{{qquad}}<math style="border:solid green 2px;padding:10px">C\left(\frac{\sqrt{2}}{2}\mathrm{,}\sqrt{2}\mathrm{,}\frac{\sqrt{2}}{2}\right)</math></center> | ||
| + | |||
| + | | ||
| + | |||
| + | <center><math>\displaystyle\vec{b}=\frac{\sqrt{2}}{2}(\vec{\imath}\ + \ \vec{k}) | ||
| + | </math>{{qquad}}{{tose}}{{qquad}}<math >\vec{c}=\vec{a}+\vec{b}=\sqrt{2}\ \vec{\imath}\ + \ \frac{\sqrt{2}}{2}\ \vec{\jmath}\ +\ \frac{\sqrt{2}}{2}\ \vec{k}</math>{{qquad}}{{tose}}{{qquad}}<math >C\left(\sqrt{2}\mathrm{,}\frac{\sqrt{2}}{2}\mathrm{,}\frac{\sqrt{2}}{2}\right)</math></center> | ||
| + | |||
| + | [[Categoría:Problemas de examen F1 GIA]] | ||
última version al 10:34 28 sep 2016
Contenido |
1 Enunciado
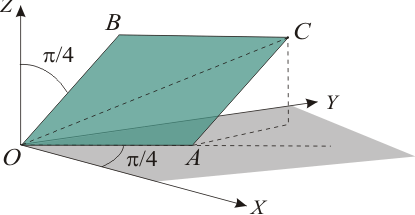
El rombo OACB tiene sus lados de longitud unidad y suárea es igual a 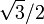 . Su lado OA se encuentra en el plano
OXY de un sistema de referencia cartesiano, formando un ángulo de
π / 4 con el eje OX. El lado OB forma un ángulo de π / 4
con el eje OZ.
. Su lado OA se encuentra en el plano
OXY de un sistema de referencia cartesiano, formando un ángulo de
π / 4 con el eje OX. El lado OB forma un ángulo de π / 4
con el eje OZ.
- Calcular la longitud de la diagonal OC
- Determinar las coordenads cartesianas del vértice C
2 Solución
2.1 Longitud de la diagonal
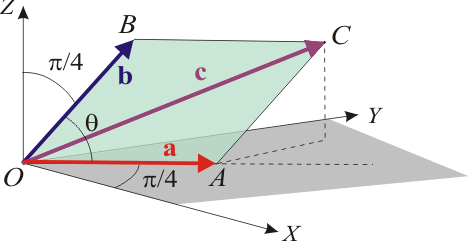
Consideremos los vectores  ,
,  y
y 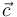 , de igual módulo, dirección y sentido que los respectivos segmentos orientados
, de igual módulo, dirección y sentido que los respectivos segmentos orientados  ,
, 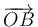 y
y  . Al corresponder éstos con dos lados adyacentes y la diagonal del rombo, se tendrán que
. Al corresponder éstos con dos lados adyacentes y la diagonal del rombo, se tendrán que
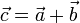
La longitud de la diagonal OC es el módulo de este vector,
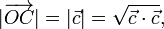
que podemos obtener a partir del producto escalar del vector por sí mismo:
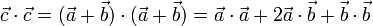
Como los lados OA y OB tienen longitud unidad, sus correspondientes vectores tienen módulo 1. Se tendrán entonces,
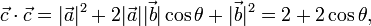
siendo θ el ángulo que forman los segmentos  y
y 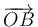 . Y para determinar el valor de dicho ángulo, utilizamos el dato del área del rombo que, al ser esta figura un paralelogramo, será igual al módulo del producto vectorial de los vectores que se corresponden con dos lados adyacentes; es decir,
. Y para determinar el valor de dicho ángulo, utilizamos el dato del área del rombo que, al ser esta figura un paralelogramo, será igual al módulo del producto vectorial de los vectores que se corresponden con dos lados adyacentes; es decir,
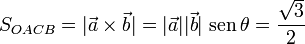
Aplicando de nuevo que los lados del rombo tienen longitud unidad y que, por tanto, los vectores  y
y  tienen módulo uno, se obtiene...
tienen módulo uno, se obtiene...
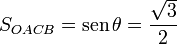

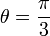
Y con este resultado ya podemos determinar la magnitud de la diagonal del rombo:
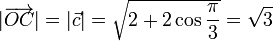
2.2 Coordenadas del vértice C
Al tomar el origen del sistema de referencia en el vértice O del rombo, las coordenadas cartesianas del vértice C son las mismas que las del vector 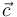 cuyo módulo dirección y sentido son los del segmento orientado
cuyo módulo dirección y sentido son los del segmento orientado  . Y, como sabemos, el vector
. Y, como sabemos, el vector 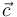 lo podemos obtener como la suma de los vectores
lo podemos obtener como la suma de los vectores  y
y  . Así que, comencemos por la obtención de las expresiones analíticas de estos dos vectores en la base cartesiana. Ambos son vectores unitarios, por tanto, sus correspondientes coordenadas cartesianas serán sus cosenos directores respecto de las direcciones OX, OY y OZ.
. Así que, comencemos por la obtención de las expresiones analíticas de estos dos vectores en la base cartesiana. Ambos son vectores unitarios, por tanto, sus correspondientes coordenadas cartesianas serán sus cosenos directores respecto de las direcciones OX, OY y OZ.
Al estar contenido en el plano OXY, el segmento orientado  forma un ángulo π / 2 con el eje OZ y, según se indica en el enunciado, sendos ángulos π / 4 con los ejes OX y OY. Por tanto,
forma un ángulo π / 2 con el eje OZ y, según se indica en el enunciado, sendos ángulos π / 4 con los ejes OX y OY. Por tanto,
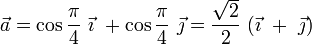
Por su parte, sabemos que el vector  forma un ángulo π / 4 con el eje OZ, pero desconocemos los ángulos α y β que forma con los ejes OX y OY; es decir, desconocemos sus componentes cartesianas “x” e “y”:
forma un ángulo π / 4 con el eje OZ, pero desconocemos los ángulos α y β que forma con los ejes OX y OY; es decir, desconocemos sus componentes cartesianas “x” e “y”:
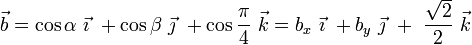
Para determinar los valores de las coordenadas desconocidas utilizaremos dos datos que conocemos: el módulo del vector  y el valor del producto escalar de este vector por el
y el valor del producto escalar de este vector por el  , a partir de los que podremos plantear sendas ecuaciones algebraicas cuya solución serán las coordenadas desconocidas del vector
, a partir de los que podremos plantear sendas ecuaciones algebraicas cuya solución serán las coordenadas desconocidas del vector  :
:
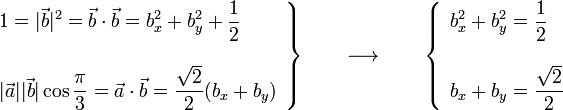
Este sistema de ecuaciones admite dos soluciones posibles. Una de ellas es:
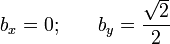
lo que implica que significa que el vector  (y el punto B), está contenido en el plano OYZ (es decir, α = π / 2), formando también un ángulo β = π / 4 con el eje OY. La otra solución es...
(y el punto B), está contenido en el plano OYZ (es decir, α = π / 2), formando también un ángulo β = π / 4 con el eje OY. La otra solución es...

Para ésta, el punto B y el vector  están incluidos en el plano OXZ (β = π / 2), y este último forma ángulos de π / 4 con los ejes OX y OZ. A cada una de estas soluciones le correponde una posición distinta del vértice C:
están incluidos en el plano OXZ (β = π / 2), y este último forma ángulos de π / 4 con los ejes OX y OZ. A cada una de estas soluciones le correponde una posición distinta del vértice C: