1.6. Dependencias de la fuerza viscosa (Ex.Nov/11)
De Laplace
(→Ley de Stokes) |
(→Ley de Stokes) |
||
| (19 ediciones intermedias no se muestran.) | |||
| Línea 20: | Línea 20: | ||
==Ley de Stokes== | ==Ley de Stokes== | ||
| - | Se nos dice que, según la ley de Stokes, la fuerza viscosa F que sufre una esfera móvil en el seno de un fluido sólo | + | Se nos dice que, según la ley de Stokes, el módulo de la fuerza viscosa <math>F\,</math> que sufre una esfera móvil en el seno de un fluido sólo es función de tres magnitudes: el radio <math>r\,</math> de la esfera, la celeridad <math>v\,</math> de la esfera, y la viscosidad dinámica <math>\eta\,</math> del fluido, es decir: |
| - | <center><math>F= | + | <center><math>F = f(r,v,\eta)\,</math></center> |
| + | Pero esta ecuación ha de ser dimensionalmente homogénea. Por tanto, <math>f\,</math> no puede ser una función arbitraria, sino que debe ser un producto de potencias de sus tres variables cuyo resultado tenga dimensiones de fuerza: | ||
| + | |||
| + | <center><math>F=K\,r^nv^p\eta^q\,</math></center> | ||
| + | |||
| + | donde <math>K\,</math> es un factor numérico adimensional que no seremos capaces de determinar mediante análisis dimensional, pero que no nos hace falta para poder responder a las preguntas que se nos plantean. | ||
| + | |||
| + | Será, pues, la exigencia de homogeneidad dimensional sobre la anterior ecuación la que nos permita deducir cuáles son los valores de los exponentes <math>n\,</math>, <math>p\,</math> y <math>q\,</math>. Tomando dimensiones en la anterior ecuación, se obtiene: | ||
| + | |||
| + | <center><math>[F] = [r]^n[v]^p[\eta]^q \,\,\,\,\,\Longrightarrow\,\,\,\,\,MLT^{-2} = L^n\left(LT^{-1}\right)^p\left(ML^{-1}T^{-1}\right)^q\,\,\,\,\,\Longrightarrow\,\,\,\,\, MLT^{-2} = M^{q}L^{n+p-q}T^{-p-q}\,</math></center> | ||
| + | |||
| + | Igualando entre sí los exponentes de cada magnitud básica en ambos miembros, obtenemos: | ||
| + | |||
| + | <center><math> 1 = q \,\,;\qquad\qquad 1 = n + p - q \,\,;\qquad\qquad -2 = -p - q </math></center> | ||
| + | |||
| + | de donde: | ||
| + | |||
| + | <center><math>n = 1\,\,;\qquad\qquad p = 1\,\,;\qquad\qquad q = 1</math></center> | ||
| + | |||
| + | y por tanto el módulo de la fuerza viscosa responde a la expresión: | ||
| + | |||
| + | <center><math>F = K\,r\, v\,\eta</math></center> | ||
| + | |||
| + | Esta expresión no nos dice cuánto vale el módulo de la fuerza viscosa, ya que desconocemos el valor del factor numérico adimensional <math>K\,</math>. Sin embargo, nos proporciona una información muy interesante: el tipo de dependencia existente entre el módulo de la fuerza viscosa y las variables <math>r\,</math>, <math>v\,</math> y <math>\eta\,</math>. De hecho, observamos que se trata de una relación de proporcionalidad directa, de tal modo que la multiplicación de cualquiera de las tres variables por un cierto factor (manteniéndose las demás constantes) se traduce en la multiplicación de la fuerza viscosa exactamente por el mismo factor. Y esto es justo lo que necesitábamos saber para poder responder a las dos cuestiones finales que se nos plantean. | ||
| + | |||
| + | No obstante, para no dejar a nadie con la curiosidad, diremos que en la ley de Stokes el factor adimensional <math>K\,</math> vale 6<math>\pi\,</math>. | ||
| + | |||
| + | ==Respuesta a las dos cuestiones finales== | ||
| + | |||
| + | a) Al tratarse de dos esferas moviéndose con igual celeridad en un mismo fluido, la única variable que cambia de una a otra es el radio, que se nos dice ser el doble en la segunda que en la primera. Por tanto, es inmediato deducir la relación entre los módulos de las fuerzas viscosas soportadas por una y otra esfera: | ||
| + | |||
| + | <center><math>r_2=2\,r_1 \,\,\,\,\,\longrightarrow\,\,\,\,\, F_2=K\, r_2\, v\,\eta=2\,K\,r_1\, v\,\eta= 2\,F_1</math></center> | ||
| + | |||
| + | b) En este caso, se trata de una única esfera móvil en el seno de un fluido, y la variable que se modifica de un instante a otro es simplemente su celeridad. Deduciremos, pues, cuál es la modificación sufrida por el módulo de la fuerza viscosa que soporta la esfera al pasar del primer al segundo instante: | ||
| + | |||
| + | <center><math>v_2=0.80\,v_1 \,\,\,\,\,\longrightarrow\,\,\,\,\, F_2=K\, r\, v_2\,\eta=0.80\,K\,r\, v_1\,\eta= 0.80\,F_1</math></center> | ||
[[Categoría:Problemas de metrología (G.I.T.I.)]] | [[Categoría:Problemas de metrología (G.I.T.I.)]] | ||
última version al 13:50 10 nov 2012
Contenido |
1 Enunciado
El poise (P), que es la unidad de viscosidad dinámica en el sistema CGS, se define como 1 P = 1 g (s
(s cm) − 1. ¿Cuál es la unidad de viscosidad dinámica en el SI?
cm) − 1. ¿Cuál es la unidad de viscosidad dinámica en el SI?
Según la denominada ley de Stokes, el módulo de la fuerza viscosa 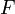 ejercida sobre una esfera que se mueve en un fluido depende exclusivamente de tres magnitudes: el radio
ejercida sobre una esfera que se mueve en un fluido depende exclusivamente de tres magnitudes: el radio  de la esfera, la celeridad
de la esfera, la celeridad  con que ésta se mueve y la viscosidad dinámica
con que ésta se mueve y la viscosidad dinámica 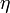 del fluido. Deduzca, mediante análisis dimensional, los exponentes
del fluido. Deduzca, mediante análisis dimensional, los exponentes 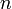 ,
, 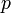 y
y 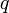 con los que aparecen
con los que aparecen  ,
,  y
y 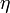 , respectivamente, en la fórmula del módulo de la fuerza viscosa según Stokes, y así podrá responder a las dos siguientes preguntas.
, respectivamente, en la fórmula del módulo de la fuerza viscosa según Stokes, y así podrá responder a las dos siguientes preguntas.
- a) Si en un mismo fluido se mueven dos esferas, ambas con igual celeridad, pero el radio de la segunda es el doble que el radio de la primera (
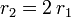 ), ¿qué relación existe entre los módulos de las fuerzas viscosas soportadas por la primera y la segunda esfera?
), ¿qué relación existe entre los módulos de las fuerzas viscosas soportadas por la primera y la segunda esfera?
- b) Si, al pasar de un instante
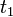 a otro posterior
a otro posterior 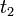 , la celeridad de una esfera en el seno de un fluido se ha reducido conforme a la relación
, la celeridad de una esfera en el seno de un fluido se ha reducido conforme a la relación 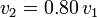 , ¿cómo habrá cambiado el módulo de la fuerza viscosa sobre ella ejercida?
, ¿cómo habrá cambiado el módulo de la fuerza viscosa sobre ella ejercida?
2 Dimensiones y unidad SI de la viscosidad dinámica
Se nos presenta el poise (P) como la unidad de viscosidad dinámica (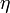 ) en cierto sistema de unidades (CGS, cegesimal). Obsérvese que, aunque no hayamos oído nunca hablar de la viscosidad dinámica, la definición de 1 poise que se nos da en el enunciado permite de inmediato deducir la ecuación dimensional de dicha magnitud física, así como su unidad en el SI. En efecto:
) en cierto sistema de unidades (CGS, cegesimal). Obsérvese que, aunque no hayamos oído nunca hablar de la viscosidad dinámica, la definición de 1 poise que se nos da en el enunciado permite de inmediato deducir la ecuación dimensional de dicha magnitud física, así como su unidad en el SI. En efecto:
![1\,\mathrm{P} = 1\,\mathrm{g}\cdot(\mathrm{s}\cdot\mathrm{cm})^{-1} \,\,\,\,\,\, \Longrightarrow \,\,\,\,\,\, [\eta]=MT^{-1}L^{-1}\,\,\,\,\,\, \Longrightarrow \,\,\,\,\,\, \mathrm{unidad}\,\, \mathrm{SI}\,\, \mathrm{de}\,\, \eta = 1\,\mathrm{kg}\cdot(\mathrm{s}\cdot\mathrm{m})^{-1}](/wiki/images/math/f/2/4/f24423a0d2be194e2b1890c0769d5ff3.png)
Pero es más frecuente expresar la unidad SI de viscosidad dinámica de este otro modo equivalente:
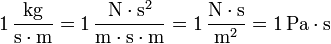
donde se ha tenido en cuenta que 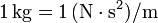 , y también que la unidad de presión en el SI es el pascal (
, y también que la unidad de presión en el SI es el pascal (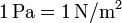 ).
).
3 Ley de Stokes
Se nos dice que, según la ley de Stokes, el módulo de la fuerza viscosa 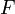 que sufre una esfera móvil en el seno de un fluido sólo es función de tres magnitudes: el radio
que sufre una esfera móvil en el seno de un fluido sólo es función de tres magnitudes: el radio  de la esfera, la celeridad
de la esfera, la celeridad  de la esfera, y la viscosidad dinámica
de la esfera, y la viscosidad dinámica 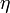 del fluido, es decir:
del fluido, es decir:
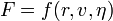
Pero esta ecuación ha de ser dimensionalmente homogénea. Por tanto, 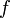 no puede ser una función arbitraria, sino que debe ser un producto de potencias de sus tres variables cuyo resultado tenga dimensiones de fuerza:
no puede ser una función arbitraria, sino que debe ser un producto de potencias de sus tres variables cuyo resultado tenga dimensiones de fuerza:

donde 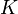 es un factor numérico adimensional que no seremos capaces de determinar mediante análisis dimensional, pero que no nos hace falta para poder responder a las preguntas que se nos plantean.
es un factor numérico adimensional que no seremos capaces de determinar mediante análisis dimensional, pero que no nos hace falta para poder responder a las preguntas que se nos plantean.
Será, pues, la exigencia de homogeneidad dimensional sobre la anterior ecuación la que nos permita deducir cuáles son los valores de los exponentes 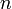 ,
, 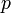 y
y 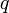 . Tomando dimensiones en la anterior ecuación, se obtiene:
. Tomando dimensiones en la anterior ecuación, se obtiene:
![[F] = [r]^n[v]^p[\eta]^q \,\,\,\,\,\Longrightarrow\,\,\,\,\,MLT^{-2} = L^n\left(LT^{-1}\right)^p\left(ML^{-1}T^{-1}\right)^q\,\,\,\,\,\Longrightarrow\,\,\,\,\, MLT^{-2} = M^{q}L^{n+p-q}T^{-p-q}\,](/wiki/images/math/0/a/5/0a56ea839fb31c6a6acaf893e55e80e0.png)
Igualando entre sí los exponentes de cada magnitud básica en ambos miembros, obtenemos:

de donde:

y por tanto el módulo de la fuerza viscosa responde a la expresión:
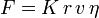
Esta expresión no nos dice cuánto vale el módulo de la fuerza viscosa, ya que desconocemos el valor del factor numérico adimensional 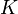 . Sin embargo, nos proporciona una información muy interesante: el tipo de dependencia existente entre el módulo de la fuerza viscosa y las variables
. Sin embargo, nos proporciona una información muy interesante: el tipo de dependencia existente entre el módulo de la fuerza viscosa y las variables  ,
,  y
y 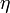 . De hecho, observamos que se trata de una relación de proporcionalidad directa, de tal modo que la multiplicación de cualquiera de las tres variables por un cierto factor (manteniéndose las demás constantes) se traduce en la multiplicación de la fuerza viscosa exactamente por el mismo factor. Y esto es justo lo que necesitábamos saber para poder responder a las dos cuestiones finales que se nos plantean.
. De hecho, observamos que se trata de una relación de proporcionalidad directa, de tal modo que la multiplicación de cualquiera de las tres variables por un cierto factor (manteniéndose las demás constantes) se traduce en la multiplicación de la fuerza viscosa exactamente por el mismo factor. Y esto es justo lo que necesitábamos saber para poder responder a las dos cuestiones finales que se nos plantean.
No obstante, para no dejar a nadie con la curiosidad, diremos que en la ley de Stokes el factor adimensional 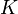 vale 6
vale 6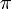 .
.
4 Respuesta a las dos cuestiones finales
a) Al tratarse de dos esferas moviéndose con igual celeridad en un mismo fluido, la única variable que cambia de una a otra es el radio, que se nos dice ser el doble en la segunda que en la primera. Por tanto, es inmediato deducir la relación entre los módulos de las fuerzas viscosas soportadas por una y otra esfera:
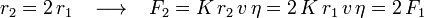
b) En este caso, se trata de una única esfera móvil en el seno de un fluido, y la variable que se modifica de un instante a otro es simplemente su celeridad. Deduciremos, pues, cuál es la modificación sufrida por el módulo de la fuerza viscosa que soporta la esfera al pasar del primer al segundo instante:






