Sistema de dos bobinas reales
De Laplace
(→Campo eléctrico inducido) |
(→Campo eléctrico inducido) |
||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 193: | Línea 193: | ||
Si consideramos una circunferencia horizontal con su centro en el eje Z, la circulación del campo eléctrico vale, en todos los casos | Si consideramos una circunferencia horizontal con su centro en el eje Z, la circulación del campo eléctrico vale, en todos los casos | ||
| - | <center><math>\oint \mathbf{E}\cdot\mathrm{d}\mathbf{r} =\int_0^{2\pi} (E(\rho)\mathbf{u}_\varphi)\cdot(\rho\,\mathrm{d}\varphi | + | <center><math>\oint \mathbf{E}\cdot\mathrm{d}\mathbf{r} =\int_0^{2\pi} (E(\rho)\mathbf{u}_\varphi)\cdot(\rho\,\mathrm{d}\varphi\,\mathbf{u}_\varphi) = 2\pi\rho\,E</math></center> |
El flujo magnético depende de si consideramos el radio de la circunferencia menor que el de las bobinas o superior a él | El flujo magnético depende de si consideramos el radio de la circunferencia menor que el de las bobinas o superior a él | ||
| Línea 200: | Línea 200: | ||
<center><math>\Phi_m =\int (B(t)\mathbf{u}_z)\cdot(\mathrm{d}S\mathbf{u}_z) = B(t)S = \pi\rho^2 B(t)</math></center> | <center><math>\Phi_m =\int (B(t)\mathbf{u}_z)\cdot(\mathrm{d}S\mathbf{u}_z) = B(t)S = \pi\rho^2 B(t)</math></center> | ||
:Derivando, cambiando el signo e igualando a la fuerza electromotriz | :Derivando, cambiando el signo e igualando a la fuerza electromotriz | ||
| - | <center><math>2\pi\rho E = -\pi \rho^2 \frac{\mathrm{d}B}{\mathrm{d}t}\qquad\Rightarrow\qquad \mathbf{E}=\frac{B_0\rho}{2\tau}\mathrm{e}^{-t\tau}\mathbf{u}_\varphi</math></center> | + | <center><math>2\pi\rho E = -\pi \rho^2 \frac{\mathrm{d}B}{\mathrm{d}t}\qquad\Rightarrow\qquad \mathbf{E}=\frac{B_0\rho}{2\tau}\mathrm{e}^{-t/\tau}\mathbf{u}_\varphi</math></center> |
| + | |||
| + | <center>[[Archivo:campo-E-bobina-1.png]] [[Archivo:campo-E-bobina-2.png]]</center> | ||
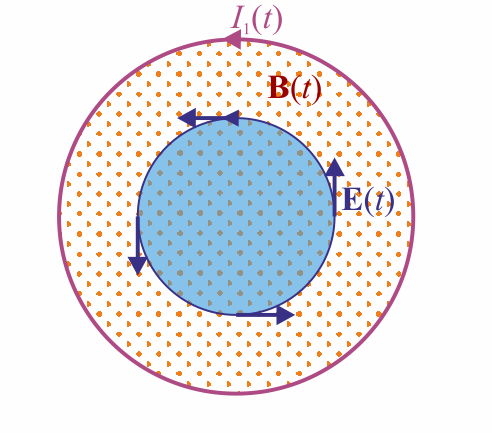
;Fuera de las bobinas: Si <math>\rho > a</math> el flujo magnético solo incluye la parte interior a las bobinas | ;Fuera de las bobinas: Si <math>\rho > a</math> el flujo magnético solo incluye la parte interior a las bobinas | ||
<center><math>\Phi_m =\int (B(t)\mathbf{u}_z)\cdot(\mathrm{d}S\mathbf{u}_z) = B(t)S = \pi a^2 B(t)</math></center> | <center><math>\Phi_m =\int (B(t)\mathbf{u}_z)\cdot(\mathrm{d}S\mathbf{u}_z) = B(t)S = \pi a^2 B(t)</math></center> | ||
:Derivando, cambiando el signo e igualando a la fuerza electromotriz | :Derivando, cambiando el signo e igualando a la fuerza electromotriz | ||
| - | <center><math>2\pi\rho E = -\pi a^2 \frac{\mathrm{d}B}{\mathrm{d}t}\qquad\Rightarrow\qquad \mathbf{E}=\frac{B_0a^2}{2\tau\rho}\mathrm{e}^{-t\tau}\mathbf{u}_\varphi</math></center> | + | <center><math>2\pi\rho E = -\pi a^2 \frac{\mathrm{d}B}{\mathrm{d}t}\qquad\Rightarrow\qquad \mathbf{E}=\frac{B_0a^2}{2\tau\rho}\mathrm{e}^{-t/\tau}\mathbf{u}_\varphi</math></center> |
Queda un campo eléctrico que en el interior de la bobina crece linealmente con la distancia al eje y fuera de ellas disminuye como la inversa de esta distancia. Tanto dentro como fuera decae exponencialmente con el tiempo. | Queda un campo eléctrico que en el interior de la bobina crece linealmente con la distancia al eje y fuera de ellas disminuye como la inversa de esta distancia. Tanto dentro como fuera decae exponencialmente con el tiempo. | ||
[[Categoría:Problemas de inducción electromagnética]] | [[Categoría:Problemas de inducción electromagnética]] | ||
última version al 14:07 2 jul 2011
Contenido |
1 Enunciado
Se arrolla un hilo de cobre de sección circular de diámetro 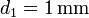 y longitud
y longitud 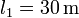 sobre un cilindro de cartón (no magnético) de radio
sobre un cilindro de cartón (no magnético) de radio  . El hilo se arrolla densamente, de forma que no queden intersticios entre vuelta y vuelta. Sobre esta capa (el primario) se arrolla otra (el secundario), en el mismo sentido, de hilo de cobre de diámetro
. El hilo se arrolla densamente, de forma que no queden intersticios entre vuelta y vuelta. Sobre esta capa (el primario) se arrolla otra (el secundario), en el mismo sentido, de hilo de cobre de diámetro 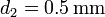 y longitud
y longitud 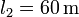 . Los extremos del secundario se dejan en circuito abierto, mientras que los del primario se conectan a una fuente de intensidad que proporciona una corriente constante
. Los extremos del secundario se dejan en circuito abierto, mientras que los del primario se conectan a una fuente de intensidad que proporciona una corriente constante 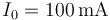 . En t = 0 se cortocircuita la fuente de intensidad mediante un hilo de resistencia despreciable.
. En t = 0 se cortocircuita la fuente de intensidad mediante un hilo de resistencia despreciable.
- Calcule las resistencias y los coeficientes de inducción mutua y autoinducción del sistema de dos bobinas.
- Determine la expresión de la corriente que circula por el primario como función del tiempo, una vez que se ha cortocircuitado la fuente. ¿Cuánto tiempo tarda, aproximadamente, en desaparecer la corriente?
- Calcule el voltaje ΔV2(t) que mide un voltímetro situado entre los extremos del secundario.
- Calcule la energía total disipada en el sistema durante el periodo transitorio en que la corriente se está atenuando hasta desaparecer.
- Determine, por aplicación de la ley de Faraday, el campo eléctrico que se induce durante el transitorio, tanto en el interior del cilindro como en puntos exteriores próximos a éste, sabiendo que es de la forma
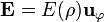 .
.

2 Resistencias y coeficientes
2.1 Resistencias
Los dos hilos son conductores filiforme, cuya resistencia puede calcularse mediante la fórmula
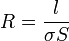
Para la primera bobina, la longitud y la conductividad valen
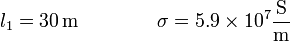
mientras que su sección es
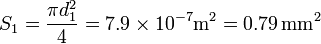
lo que nos da una resistencia

El segundo hilo tiene el doble de longitud y la cuarta parte de la sección, por lo que su resistencia es el óctuple de la anterior
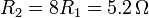
2.2 Coeficientes de autoinducción
Al enrollarlos, cada uno de los cables forma una bobina cilíndrica.
El número de vueltas de cada bobina lo obtenemos dividiendo la longitud total por la longitud de cada vuelta

Para el secundario suponemos despreciable el milímetro que se añade en el grosor, lo que nos da el número de vueltas
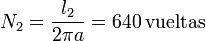
La altura de cada bobina, por estar arrolladas densamente, es igual al número de vueltas multiplicado por el grosor de cada una, que es el diámetro del cable

El secundario tiene la misma altura, por ser el cable de doble longitud y mitad de diámetro.
Al ser su altura 20 veces su radio, podemos hacer la aproximación de bobinas largas y calcular su coeficiente de autoinducción según la fórmula

Aquí S no es la sección transversal del cable, calculada anteriormente, sino la de la bobina circular

Esto nos da el coeficiente de autoinducción para el primario
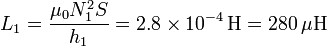
Para el secundario el cálculo es idéntico salvo que el número de espiras es el doble
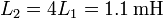
Podemos calcular estos coeficientes omitiendo los cálculos números intermedios
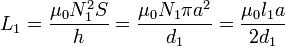
que, sustituyendo, nos da el valor que ya conocemos.
2.3 Coeficiente de inducción mutua
Para el coeficiente de inducción mutua, podemos emplear varios métodos de cálculo:
- A partir del coeficiente de acoplamiento
- Por la disposición de las dos bobinas, todo el flujo de una pasa a través de la otra, por lo que el coeficiente de acoplamiento es la unidad
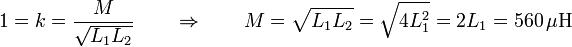
- A partir del flujo magnético
- El flujo a través del secundario del campo magnético debido al primario es N2 veces el que atraviesa cada espira
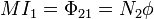
- y para el mismo campo, el flujo que atraviesa la propia bobina 1 es N1 veces el que atraviesa cada una de las espiras
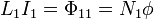
- Dividiendo una expresión por la otra
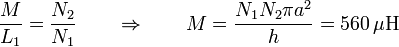
Este coeficiente también puede hallarse explícitamente empleando el valor del campo magnético producido por una de las bobinas, y hallando el flujo a través de la otra.
En forma matricial tenemos
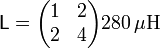
A partir de esta matriz se hallan los flujos que atraviesan cada una de las bobinas como

3 Evolución de la corriente
Inicialmente tenemos una corriente 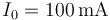 circulando por el primario, mientras que por el secundario, que está en circuito abierto no fluye corriente alguna.
circulando por el primario, mientras que por el secundario, que está en circuito abierto no fluye corriente alguna.
Una vez que se cortocircuita la fuente, tenemos en el primario una malla cerrada, en la cual se cumple

lo que nos da la ecuación para la corriente

o equivalentemente, como se suele escribir el teoría de circuitos
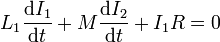
Ahora bien, el secundario se encuentra en circuito abierto en todo momento, por lo que para tod instante

lo que nos deja con la ecuación diferencial
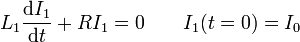
La solución de esta ecuación de coeficientes constantes, que además es separable, es inmediata,
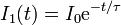
siendo τ el tiempo típico de relajación
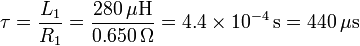
Puesto que la corriente decae exponencialmente, este es el tiempo necesario para que la corriente se reduzca en un factor 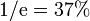 . Podemos considerar que la corriente ha desaparecido en un tiempo 2 o 3 veces τ, esto es, en torno a 1 ms.
. Podemos considerar que la corriente ha desaparecido en un tiempo 2 o 3 veces τ, esto es, en torno a 1 ms.
4 Voltaje en el secundario
Si ahora calculamos la fuerza electromotriz en el secundario, considerando la malla que forma este con el voltímetro obtenemos
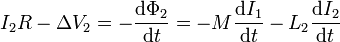
Despejando llegamos al resultado de teoría de circuitos

Sin embargo, como hemos dicho anteriormente, la corriente en el secundario es nula, por lo que el voltaje se reduce a
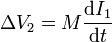
Sustituyendo la solución para la corriente obtenemos que la tensión también decae exponencialmente a partir de t = 0 (antes es nula)
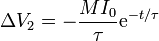
La amplitud del voltaje vale, numéricamente,

5 Energía total disipada
Para hallar la energ´ñia total disipada, tenemos dos métodos equivalentes
5.1 A partir de la energía almacenada
La energía que se disipa en el transitorio es la que había previamente almacenada en el sistema de dos biobinas. Esta energía es

Sustituyendo los valores
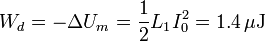
Vemos que la energía almacenada es baja por la pequeñez del coeficiente de autoinducción.
5.2 Empleando la ley de Joule
Aunque es un poco más largo, también puede hallarse la energía disipada a partir de la ley de Joule. La potencia disipada en cada instante es
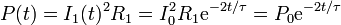
siendo la amplitud de la potencia
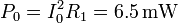
Integrando ahora sobre todo el periodo transitorio
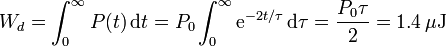
6 Campo eléctrico inducido
El campo inducido se debe al campo magnético variable en el tiempo. Este campo es debido a la corriente que circula por el primario y tiene aproximadamente el valor, expresado en coordenadas cilíndricas centradas en el eje de las bobinas,
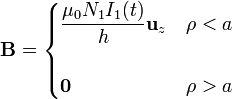
Tenemos entonces un campo uniforme, pero no constante, en el interior de las bobinas, que decae exponencialmente como
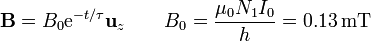
Este campo magnético induce un campo eléctrico que verifica
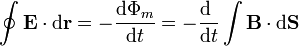
Si consideramos una circunferencia horizontal con su centro en el eje Z, la circulación del campo eléctrico vale, en todos los casos

El flujo magnético depende de si consideramos el radio de la circunferencia menor que el de las bobinas o superior a él
- Dentro de las bobinas
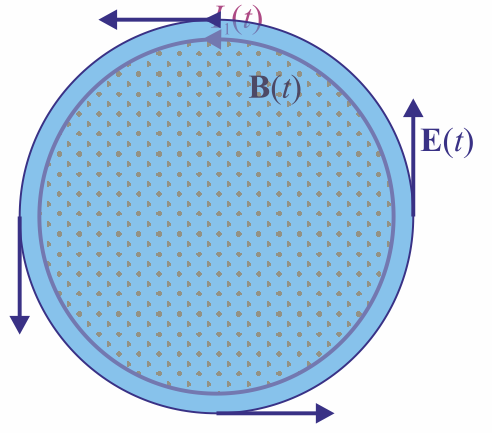
- Si ρ < a
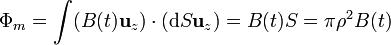
- Derivando, cambiando el signo e igualando a la fuerza electromotriz
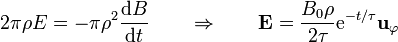
- Fuera de las bobinas
- Si ρ > a el flujo magnético solo incluye la parte interior a las bobinas
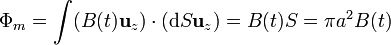
- Derivando, cambiando el signo e igualando a la fuerza electromotriz
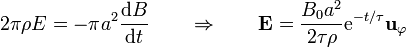
Queda un campo eléctrico que en el interior de la bobina crece linealmente con la distancia al eje y fuera de ellas disminuye como la inversa de esta distancia. Tanto dentro como fuera decae exponencialmente con el tiempo.





