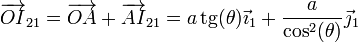6.2. Movimiento de barra en un pasador
De Laplace
(→Velocidades) |
|||
| (11 ediciones intermedias no se muestran.) | |||
| Línea 65: | Línea 65: | ||
==Velocidades y aceleraciones== | ==Velocidades y aceleraciones== | ||
===Velocidades=== | ===Velocidades=== | ||
| - | La velocidad del punto A podemos hallarla derivando su vector posición que nos es conocido en cada instante | + | ====Conocido el CIR==== |
| + | Si hemos sido capaces de localizar el CIR del movimiento, la velocidad instantánea de cualquier punto puede hallarse según la expresión del campo de velocidades | ||
| + | |||
| + | <center><math>\vec{v}^A_{21}=\omega_{21}\vec{k}\times\overrightarrow{I_{21}A}</math></center> | ||
| + | |||
| + | La velocidad angular del movimiento es igual a la derivada temporal del ángulo que forman los ejes <math>OX_1</math> y <math>OX_2</math>. Este ángulo es igual al que forman los ejes <math>OY_1</math> e <math>OY_2</math>, que el ángulo <math>\theta</math> representado en la figura. | ||
| + | |||
| + | <center><math>\omega_{21}=\dot{\theta}</math></center> | ||
| + | |||
| + | El vector de posición relativo de A es el opuesto del calculado en el apartado anterior. De aquí, hallamos la velocidad | ||
| + | |||
| + | <center><math>\vec{v}^A_{21} = \dot{\theta}\vec{k}\left(-\frac{a}{\cos^2(\theta)}\vec{\jmath}_1\right) =\frac{a\dot{\theta}}{\cos^2(\theta)}\vec{\imath}_1</math></center> | ||
| + | |||
| + | Sustituyendo la ley horaria | ||
| + | |||
| + | <center><math>\vec{v}^A_{21} = \frac{a\Omega}{\cos^2(\Omega t)}\vec{\imath}_1</math></center> | ||
| + | |||
| + | ====Por derivación==== | ||
| + | La velocidad del punto A también podemos hallarla derivando su vector posición que nos es conocido en cada instante | ||
<center><math>\overrightarrow{OA}=a\,\mathrm{tg}(\theta)\vec{\imath}_1 = a\,\mathrm{tg}(\Omega t)\vec{\imath}_1</math></center> | <center><math>\overrightarrow{OA}=a\,\mathrm{tg}(\theta)\vec{\imath}_1 = a\,\mathrm{tg}(\Omega t)\vec{\imath}_1</math></center> | ||
| Línea 73: | Línea 91: | ||
<center><math>\vec{v}^A_{21}=\left.\frac{\mathrm{d}\ }{\mathrm{d}t}\overrightarrow{OA}\right|_1=\frac{a\Omega}{\cos^2(\Omega t)}\vec{\imath}_1</math></center> | <center><math>\vec{v}^A_{21}=\left.\frac{\mathrm{d}\ }{\mathrm{d}t}\overrightarrow{OA}\right|_1=\frac{a\Omega}{\cos^2(\Omega t)}\vec{\imath}_1</math></center> | ||
| + | ====Velocidad de B==== | ||
Para la velocidad de B podemos usar la expresión del campo de velocidades de un sólido rígido | Para la velocidad de B podemos usar la expresión del campo de velocidades de un sólido rígido | ||
| Línea 91: | Línea 110: | ||
y obtenemos | y obtenemos | ||
| - | <center><math>\vec{v}^B_{21} = \left(\frac{a\Omega}{\cos^2(\Omega t)}-2a\cos(\Omega t)\right)\vec{\imath}_1-2a\Omega\,\mathrm{sen}(\Omega t)\vec{\jmath}_1</math></center> | + | <center><math>\vec{v}^B_{21} = \left(\frac{a\Omega}{\cos^2(\Omega t)}-2a\Omega \cos(\Omega t)\right)\vec{\imath}_1-2a\Omega\,\mathrm{sen}(\Omega t)\vec{\jmath}_1</math></center> |
La velocidad de B también podemos obtenerla mediante derivación de la posición, ya que no es difícil hallar el vector de posición relativa | La velocidad de B también podemos obtenerla mediante derivación de la posición, ya que no es difícil hallar el vector de posición relativa | ||
| - | <center><math>\overrightarrow{OB}=\ | + | <center><math>\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}=\left(a\,\mathrm{tg}(\Omega t)-2a\,\mathrm{sen}(\Omega t)\right)\vec{\imath}_1+2a\cos(\Omega t)\vec{\jmath}_1</math></center> |
Derivando aquí respecto al tiempo reobtenemos el resultado anterior. | Derivando aquí respecto al tiempo reobtenemos el resultado anterior. | ||
| + | |||
| + | ===Aceleraciones=== | ||
| + | La aceleración de A la hallamos derivando de nuevo respecto al tiempo | ||
| + | |||
| + | <center><math>\vec{a}^A_{21} = \left.\frac{\mathrm{d}\vec{v}^A_{21}}{\mathrm{d}t}\right|_1=\frac{2a\Omega^2\mathrm{sen}(\Omega t)}{\cos^3(\Omega t)}\vec{\imath}_1</math></center> | ||
| + | |||
| + | Para la aceleración de B aplicamos la expresión del campo de aceleraciones | ||
| + | |||
| + | <center><math>\vec{a}^B_{21} = \vec{a}^A_{21}+\alpha_{21}\vec{k}\times\overrightarrow{AB}-\omega_{21}^2\overrightarrow{AB}</math></center> | ||
| + | |||
| + | La aceleración angular es nula, por ser constante la velocidad angular. Obtenemos entonces la aceleracióin | ||
| + | |||
| + | <center><math>\vec{a}^B_{21}= \frac{2a\Omega^2\mathrm{sen}(\Omega t)}{\cos^3(\Omega t)}\vec{\imath}_1-2a\Omega^2\vec{\jmath}_2</math></center> | ||
| + | |||
| + | Pasando a una única base la expresamos como | ||
| + | |||
| + | <center><math>\vec{a}^B_{21}= \left(\frac{2a\Omega^2\mathrm{sen}(\Omega t)}{\cos^3(\Omega t)}+2a\Omega^2\mathrm{sen}(\Omega t)\right)\vec{\imath}_1-2a\Omega^2\cos(\Omega t)\vec{\jmath}_1</math></center> | ||
| + | |||
| + | Esta aceleración también puede calcularse por derivación de la velocidad calculada en el apartado anterior. | ||
==Obtención analítica del CIR== | ==Obtención analítica del CIR== | ||
| + | Aunque en el primer apartado ya obtuvimos, por razonamientos geométricos la ecuación para la posición del CIR, también podemos llegar a ésta por aplicación de la fórmula | ||
| + | |||
| + | <center><math>\overrightarrow{AI}_{21}=\frac{\vec{k}\times\vec{v}^A_{21}}{\omega_{21}}</math></center> | ||
| + | |||
| + | Sustituimos la expresión de las velocidades que hemos calculado previamente | ||
| + | |||
| + | <center><math>\overrightarrow{AI}_{21}=\frac{\vec{k}\times((a\Omega/\cos^2(\Omega t))\vec{\imath}_1)}{\Omega}=\frac{a}{\cos^2(\Omega t)}\vec{\jmath}_1=\frac{a}{\cos^2(\theta)}\vec{\jmath}_1</math></center> | ||
| + | |||
| + | que es la expresión que ya conocemos. respecto al punto O, esta posición es, según vimos | ||
| + | |||
| + | <center><math>\overrightarrow{OI}_{21}=\overrightarrow{OA}+\overrightarrow{AI}_{21}=a\,\mathrm{tg}(\theta)\vec{\imath}_1+\frac{a}{\cos^2(\theta)}\vec{\jmath}_1</math></center> | ||
| + | |||
[[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | [[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | ||
última version al 13:24 24 sep 2013
Contenido[ocultar] |
1 Enunciado
La barra AB (sólido “2”), de longitud 2a, puede deslizar en su extremo A por el eje OX1 de la escuadra fija OX1Y1 (sólido “1”), al mismo tiempo que desliza por el interior de un pasador orientable ubicado en el punto C del eje OY1, a una distancia a del origen O. Sabiendo que la barra gira con velocidad angular constante Ω (ley horaria θ(t) = Ωt, donde θ es el ángulo definido en la figura), se pide:
- Determinar gráficamente la posición del centro instantáneo de rotación (CIR) del movimiento {21}.
- Calcular las velocidades,
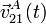 y
y 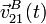 , y las aceleraciones,
, y las aceleraciones, 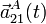 y
y 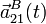 , de los dos extremos de la barra en cualquier instante de tiempo.
, de los dos extremos de la barra en cualquier instante de tiempo.
- Determinar analíticamente la posición del C.I.R. del movimiento {21}.
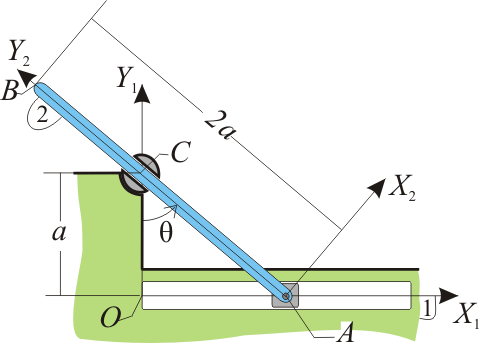
2 Determinación gráfica del CIR
En la mayoría de los problemas de movimiento plano, existe más de una forma de determinar geométricamente la posición del centro instantáneo de rotación.
El procedimiento habitual suele ser buscar dos puntos para los cuales se conoce la dirección de la velocidad, trazar las perpendiculares a estas direcciones y localizar la intersección de estas rectas.
Alternativamente, con ayuda del teorema de los tres centros, puede sustituirse alguna (o las dos) de las rectas perpendiculares anteriores por una recta que pasa por dos CCIIR conocidos.
En este problema tenemos un punto del cual es inmediata la dirección de movimiento: el punto A se mueve según una recta horizontal, de forma que
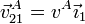
El CIR se encontrará entonces según la perpendicular por A a esta velocidad. Esta perpendicular es una recta paralela al eje OY1.
Como segundo punto consideramos el punto C en el que la barra se encuentra vinculada. El pasador establece un vínculo bilateral que impide que la barra se mueva perpendicularmente a sí misma (ya que en ese caso chocaría con el pasador). Por tanto la velocidad de C es a lo largo de la propia barra
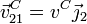
Trazamos entonces la perpendicular a la barra por C, resultando una recta paralela al eje OX2.
La intersección de estas dos rectas nos da el centro instantáneo de rotación. Este punto está situado sobre la vertical de A en el sistema “1”. Podemos hallar la altura a la que se encuentra por simples razonamientos trigonométricos.
La altura a que da el enunciado es el cateto contiguo de un triángulo con ángulo θ en el vértice. la hipotenusa de este triángulo vale
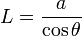
A su vez este lado es un cateto contiguo de otro triángulo rectángulo con el mismo ángulo θ. Esto nos da la altura
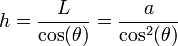
El vector de posición relativo al punto A es entonces

Para hallar el vector de posición relativo al origen sumamos la posición relativa de A
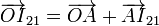
Esta posición la obtenemos de nuevo aplicando trigonometría
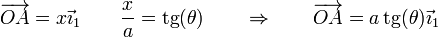
y el vector de posición relativa del CIR es
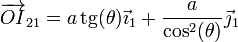
También podemos hallar la posición del CIR en el sistema 2 por razonamientos trigonométricos. La distancia entre C y el CIR la da el cateto opuesto del segundo triángulo anterior, por lo que
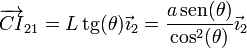
y, respecto al origen A del sistema “2”
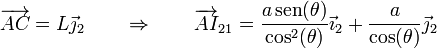
3 Velocidades y aceleraciones
3.1 Velocidades
3.1.1 Conocido el CIR
Si hemos sido capaces de localizar el CIR del movimiento, la velocidad instantánea de cualquier punto puede hallarse según la expresión del campo de velocidades
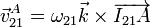
La velocidad angular del movimiento es igual a la derivada temporal del ángulo que forman los ejes OX1 y OX2. Este ángulo es igual al que forman los ejes OY1 e OY2, que el ángulo θ representado en la figura.
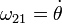
El vector de posición relativo de A es el opuesto del calculado en el apartado anterior. De aquí, hallamos la velocidad
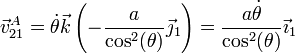
Sustituyendo la ley horaria
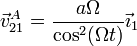
3.1.2 Por derivación
La velocidad del punto A también podemos hallarla derivando su vector posición que nos es conocido en cada instante
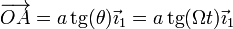
y obtenemos el resultado

3.1.3 Velocidad de B
Para la velocidad de B podemos usar la expresión del campo de velocidades de un sólido rígido
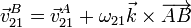
siendo
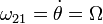

y llegamos a la velocidad
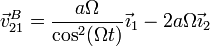
Esta expresión, aunque correcta, tiene el inconveniente de que combina dos bases diferentes. Para escribirla en una sola base aplicamos que
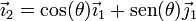

y obtenemos

La velocidad de B también podemos obtenerla mediante derivación de la posición, ya que no es difícil hallar el vector de posición relativa
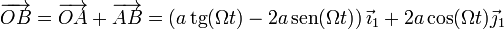
Derivando aquí respecto al tiempo reobtenemos el resultado anterior.
3.2 Aceleraciones
La aceleración de A la hallamos derivando de nuevo respecto al tiempo
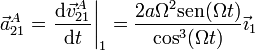
Para la aceleración de B aplicamos la expresión del campo de aceleraciones
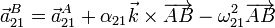
La aceleración angular es nula, por ser constante la velocidad angular. Obtenemos entonces la aceleracióin
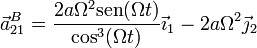
Pasando a una única base la expresamos como
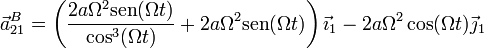
Esta aceleración también puede calcularse por derivación de la velocidad calculada en el apartado anterior.
4 Obtención analítica del CIR
Aunque en el primer apartado ya obtuvimos, por razonamientos geométricos la ecuación para la posición del CIR, también podemos llegar a ésta por aplicación de la fórmula

Sustituimos la expresión de las velocidades que hemos calculado previamente
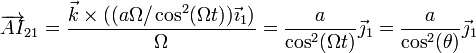
que es la expresión que ya conocemos. respecto al punto O, esta posición es, según vimos