Dos discos rodando en aro
De Laplace
(→Centros instantáneos de rotación) |
|||
| (21 ediciones intermedias no se muestran.) | |||
| Línea 13: | Línea 13: | ||
El enunciado nos da la velocidad angular con la que gira el punto C, centro del disco <math>1</math> alrededor del centro del aro “0”. Este punto pertenece tanto al sólido “1” como al “3” por tratarse de la articulación de la barra con el disco. Esta velocidad angular es la que posee toda la barra “3” en su rotación alrededor de O. Por eso, los subíndices del dato se refieren al movimiento {30} (y no al {10} ya que como veremos, el disco 1 posee una velocidad angular diferente): | El enunciado nos da la velocidad angular con la que gira el punto C, centro del disco <math>1</math> alrededor del centro del aro “0”. Este punto pertenece tanto al sólido “1” como al “3” por tratarse de la articulación de la barra con el disco. Esta velocidad angular es la que posee toda la barra “3” en su rotación alrededor de O. Por eso, los subíndices del dato se refieren al movimiento {30} (y no al {10} ya que como veremos, el disco 1 posee una velocidad angular diferente): | ||
| - | <center><math>\omega_{30}=1. | + | <center><math>\omega_{30}=1.50\frac{\mathrm{m}}{\mathrm{s}}</math></center> |
===Movimiento {10}=== | ===Movimiento {10}=== | ||
Para hallar la velocidad angular observamos que este movimiento es una rotación alrededor del punto de contacto, A, y por tanto la velocidad del centro del disco “1” en este movimiento es | Para hallar la velocidad angular observamos que este movimiento es una rotación alrededor del punto de contacto, A, y por tanto la velocidad del centro del disco “1” en este movimiento es | ||
| - | <center><math>\vec{v}^C_{10}=\ | + | <center><math>\vec{v}^C_{10}=\omega_{10}\vec{k}\times\overrightarrow{AC}</math></center> |
Por otro lado tenemos que la velocidad de C, considerado como parte de “3”, es una rotación alrededor de O | Por otro lado tenemos que la velocidad de C, considerado como parte de “3”, es una rotación alrededor de O | ||
| - | <center><math>\vec{v}^C_{10}=\vec{v}^C_{13}+\vec{v}^C_{30}=\vec{0}+\ | + | <center><math>\vec{v}^C_{10}=\vec{v}^C_{13}+\vec{v}^C_{30}=\vec{0}+\omega_{30}\vec{k}\times\overrightarrow{OC}</math></center> |
Igualando ambas velocidades llegamos a la relación | Igualando ambas velocidades llegamos a la relación | ||
| Línea 30: | Línea 30: | ||
Los vectores de posición relativos valen, en el sistema de referencia indicado: | Los vectores de posición relativos valen, en el sistema de referencia indicado: | ||
| - | <center><math>\overrightarrow{OC}=(R_0-R_1)\vec{\imath}= | + | <center><math>\overrightarrow{OC}=(R_0-R_1)\vec{\imath}_3=60\vec{\imath}_3\,\mathrm{cm}</math>{{qquad}}{{qquad}}<math>\overrightarrow{AC}=-R_1\vec{\imath}_3=-40\,\vec{\imath}_3\,\mathrm{cm}</math></center> |
De aquí obtenemos la velocidad angular | De aquí obtenemos la velocidad angular | ||
| - | <center><math>\omega_{10}=-\frac{ | + | <center><math>\omega_{10}=-\frac{60}{40}1.50\,\frac{\mathrm{rad}}{\mathrm{s}}=-2.25\,\frac{\mathrm{rad}}{\mathrm{s}}</math></center> |
===Movimiento {31}=== | ===Movimiento {31}=== | ||
| Línea 44: | Línea 44: | ||
El punto D, centro del disco “2” también gira alrededor de O con la misma velocidad angular que C. Considerado como parte del sólido “3” su velocidad lineal es | El punto D, centro del disco “2” también gira alrededor de O con la misma velocidad angular que C. Considerado como parte del sólido “3” su velocidad lineal es | ||
| - | <center><math>\vec{v}^D_{30}=\ | + | <center><math>\vec{v}^D_{30}=\omega_{30}\vec{k}\times\overrightarrow{OD}</math></center> |
mientras que, considerado como parte del disco “2” realiza una rotación instantánea alrededor del punto B, de contacto del disco con el aro. | mientras que, considerado como parte del disco “2” realiza una rotación instantánea alrededor del punto B, de contacto del disco con el aro. | ||
| - | <center><math>\vec{v}^D_{20}=\ | + | <center><math>\vec{v}^D_{20}=\omega_{20}\vec{k}\times\overrightarrow{BD}</math></center> |
Estas dos velocidades deben ser iguales, ya que | Estas dos velocidades deben ser iguales, ya que | ||
| Línea 58: | Línea 58: | ||
<center><math>\omega_{30}\overrightarrow{OD}=\omega_{20}\overrightarrow{BD}</math></center> | <center><math>\omega_{30}\overrightarrow{OD}=\omega_{20}\overrightarrow{BD}</math></center> | ||
| - | Aunque para determinar la velocidad angular nos basta con saber que los vectores de posición son proporcionales y de | + | Aunque para determinar la velocidad angular nos basta con saber que los vectores de posición son proporcionales y de sentido opuesto, vamos a determinar su expresión en el sistema de referencia indicado, ya que ésta puede ser útil más adelante. |
| - | La figura sugiere que los puntos B y D se encuentran sobre el eje <math>OY_3</math>, no tenemos certeza de tal afirmación. De hecho, para valores arbitrarios de <math>R_1</math>, <math>R_2</math> y <math>L</math> no será cierto en general. Vamos a demostrar que sí ocurre para los datos del enunciado. Para ello, hemos de probar que el ángulo COD es recto. | + | La figura sugiere que los puntos B y D se encuentran sobre el eje <math>OY_3</math>. Sin embargo, no tenemos certeza de tal afirmación. De hecho, para valores arbitrarios de <math>R_1</math>, <math>R_2</math> y <math>L</math> no será cierto en general. Vamos a demostrar que sí ocurre para los datos del enunciado. Para ello, hemos de probar que el ángulo COD es recto. |
En el triángulo OCD los lados valen | En el triángulo OCD los lados valen | ||
| - | <center><math>|\overrightarrow{OC}|=R_0-R_1= | + | <center><math>|\overrightarrow{OC}|=R_0-R_1=60\,\mathrm{cm}</math>{{qquad}}{{qquad}}<math>|\overrightarrow{OD}|=R_0-R_2=80\,\mathrm{cm}</math>{{qquad}}{{qquad}}<math>|\overrightarrow{CD}|=L=100\,\mathrm{cm}</math></center> |
Aplicando el teorema del coseno tenemos que si <math>\gamma</math> es el ángulo en O | Aplicando el teorema del coseno tenemos que si <math>\gamma</math> es el ángulo en O | ||
| - | <center><math>\cos(\gamma)=\frac{|\overrightarrow{OC}|^2+|\overrightarrow{OD}|^2-|\overrightarrow{CD}|^2}{2|\overrightarrow{OC}||\overrightarrow{OD}|}=\frac{ | + | <center><math>\cos(\gamma)=\frac{|\overrightarrow{OC}|^2+|\overrightarrow{OD}|^2-|\overrightarrow{CD}|^2}{2|\overrightarrow{OC}||\overrightarrow{OD}|}=\frac{60^2+80^2-100^2}{2\cdot 60\cdot 80}=0</math></center> |
Por tanto el ángulo es efectivamente recto y los vectores de posición relativos son | Por tanto el ángulo es efectivamente recto y los vectores de posición relativos son | ||
| - | <center><math>\overrightarrow{OD}= | + | <center><math>\overrightarrow{OD}=80\,\vec{\jmath}_3\,\mathrm{cm}</math>{{qquad}}{{qquad}}<math>\overrightarrow{BD}=-20\vec{\jmath}_3\,\mathrm{cm}</math></center> |
y la velocidad angular del movimiento {20} valen | y la velocidad angular del movimiento {20} valen | ||
| - | <center><math>\omega_{20}=-\frac{ | + | <center><math>\omega_{20}=-\frac{80}{20}1.50\,\frac{\mathrm{rad}}{\mathrm{s}}=-6.00\,\frac{\mathrm{rad}}{\mathrm{s}}</math></center> |
===Movimiento {32}=== | ===Movimiento {32}=== | ||
De nuevo empleamos la ley de composición de velocidades angulares para hallar la del movimiento {32} | De nuevo empleamos la ley de composición de velocidades angulares para hallar la del movimiento {32} | ||
| - | <center><math>\omega_{32}=\omega_{30}+\omega_{02}=\omega_{30}-\omega_{20}=7.50\,\frac{\mathrm{ | + | <center><math>\omega_{32}=\omega_{30}+\omega_{02}=\omega_{30}-\omega_{20}=7.50\,\frac{\mathrm{rad}}{\mathrm{s}}</math></center> |
===Movimiento {21}=== | ===Movimiento {21}=== | ||
| - | Por último, para hallar la velocidad angular con la que gira un disco respecto al otro empleamos de nuevo la ley de composición de velocidades empleando el aro | + | Por último, para hallar la velocidad angular con la que gira un disco respecto al otro empleamos de nuevo la ley de composición de velocidades empleando el aro “0” como sólido intermedio |
| - | <center><math>\omega_{21}=\omega_{20}+\omega_{01}=\omega_{20}-\omega_{10}=\left(-6.00+2.25\right)\,\frac{\mathrm{ | + | <center><math>\omega_{21}=\omega_{20}+\omega_{01}=\omega_{20}-\omega_{10}=\left(-6.00+2.25\right)\,\frac{\mathrm{rad}}{\mathrm{s}}=-3.75\,\frac{\mathrm{rad}}{\mathrm{s}}</math></center> |
| - | Alternativamente, podemos emplear la barra | + | Alternativamente, podemos emplear la barra “3” como sólido intermedio |
| - | <center><math>\omega_{21}=\omega_{23}+\omega_{31}=-\omega_{32}+\omega_{31}=\left(-7.50+3.75\right)\,\frac{\mathrm{ | + | <center><math>\omega_{21}=\omega_{23}+\omega_{31}=-\omega_{32}+\omega_{31}=\left(-7.50+3.75\right)\,\frac{\mathrm{rad}}{\mathrm{s}}=-3.75\,\frac{\mathrm{rad}}{\mathrm{s}}</math></center> |
==Centros instantáneos de rotación== | ==Centros instantáneos de rotación== | ||
| Línea 109: | Línea 109: | ||
:En forma vectorial | :En forma vectorial | ||
| - | <center><math>\overrightarrow{OI}_{31}= | + | <center><math>\overrightarrow{OI}_{31}=60\,\vec{\imath}_3\,\mathrm{cm}</math></center> |
;Movimiento {23}: Análogamente, el disco “2” ejecuta, respecto de la barra “3”, una rotación alrededor de su centro: | ;Movimiento {23}: Análogamente, el disco “2” ejecuta, respecto de la barra “3”, una rotación alrededor de su centro: | ||
| Línea 117: | Línea 117: | ||
:En forma vectorial | :En forma vectorial | ||
| - | <center><math>\overrightarrow{OI}_{32}= | + | <center><math>\overrightarrow{OI}_{32}=80\,\vec{\jmath}_3\,\mathrm{cm}</math></center> |
;Movimiento {10}: Dado que el contacto entre el disco 1 y el aro 0 implica rodadura sin deslizamiento, el CIR del movimiento es el punto de contacto | ;Movimiento {10}: Dado que el contacto entre el disco 1 y el aro 0 implica rodadura sin deslizamiento, el CIR del movimiento es el punto de contacto | ||
| Línea 125: | Línea 125: | ||
:En forma vectorial | :En forma vectorial | ||
| - | <center><math>\overrightarrow{OI}_{10}= | + | <center><math>\overrightarrow{OI}_{10}=100\,\vec{\imath}_3\,\mathrm{cm}</math></center> |
;Movimiento {20}: El disco “2” también realiza, respecto del aro “0”, una rotación instantánea alrededor del punto de contacto, por lo que | ;Movimiento {20}: El disco “2” también realiza, respecto del aro “0”, una rotación instantánea alrededor del punto de contacto, por lo que | ||
| Línea 133: | Línea 133: | ||
:En forma vectorial | :En forma vectorial | ||
| - | <center><math>\overrightarrow{OI}_{20}= | + | <center><math>\overrightarrow{OI}_{20}=100\,\vec{\jmath}_3\,\mathrm{cm}</math></center> |
;Movimiento {21}: Este es el único que no es evidente. Podemos hallar este punto analítica y gráficamente. Para calcularlo de manera analítica precisamos la velocidad de un punto. Si queremos la posición respecto al punto O, la fórmula correspondiente es | ;Movimiento {21}: Este es el único que no es evidente. Podemos hallar este punto analítica y gráficamente. Para calcularlo de manera analítica precisamos la velocidad de un punto. Si queremos la posición respecto al punto O, la fórmula correspondiente es | ||
| Línea 139: | Línea 139: | ||
<center><math>\overrightarrow{OI}_{21}=\frac{\vec{k}\times\vec{v}^O_{21}}{\omega_{21}}</math></center> | <center><math>\overrightarrow{OI}_{21}=\frac{\vec{k}\times\vec{v}^O_{21}}{\omega_{21}}</math></center> | ||
| - | Necesitamos la velocidad del punto O en el movimiento {21}. La obtenemos aplicando la fórmula de composición de velocidades. Los movimientos {20} y {10} son rotaciones instantáneas alrededor de los puntos B y A por lo que | + | :Necesitamos la velocidad del punto O en el movimiento {21}. La obtenemos aplicando la fórmula de composición de velocidades. Los movimientos {20} y {10} son rotaciones instantáneas alrededor de los puntos B y A por lo que |
| - | <center><math>\vec{v}^O_{21}=\vec{v}^O_{20}-\vec{v}^O_{ | + | <center><math>\vec{v}^O_{21}=\vec{v}^O_{20}-\vec{v}^O_{10}=\omega_{20}\vec{k}\times\overrightarrow{BO}-\omega_{10}\vec{k}\times\overrightarrow{AO}</math></center> |
| - | Sustituyendo los valores numéricos | + | :Sustituyendo los valores numéricos |
| - | <center><math>\vec{v}^O_{21}=\left(-6.00\vec{k}\frac{\mathrm{rad}{\mathrm{s}}\right)\times(-100\,\vec{\jmath}\,\mathrm{cm})-\left(-2.25\vec{k}\frac{\mathrm{rad}{\mathrm{s}}\right)\times(-100\,\vec{\imath}\,\mathrm{cm})=\left(-600\,\vec{\imath}-225\,\vec{\jmath}\right)\,\frac{\mathrm{cm}}{\mathrm{s}}</math></center> | + | <center><math>\vec{v}^O_{21}=\left(-6.00\vec{k}\frac{\mathrm{rad}}{\mathrm{s}}\right)\times(-100\,\vec{\jmath}_3\,\mathrm{cm})-\left(-2.25\vec{k}\frac{\mathrm{rad}}{\mathrm{s}}\right)\times(-100\,\vec{\imath}_3\,\mathrm{cm})=\left(-600\,\vec{\imath}_3-225\,\vec{\jmath}_3\right)\,\frac{\mathrm{cm}}{\mathrm{s}}</math></center> |
| - | Llevando esto a la expresión analítica del CIR nos queda | + | :Llevando esto a la expresión analítica del CIR nos queda |
| - | <center><math>\overrightarrow{OI}_{21}=\frac{\vec{k}\times\left(-600\,\vec{\imath} | + | <center><math>\overrightarrow{OI}_{21}=\frac{\vec{k}\times\left(-600\,\vec{\imath}_3-225\,\vec{\jmath}_3\right)}{-3.75}\,\mathrm{cm}=\left(-60\vec{\imath}_3+160\vec{\jmath}_3\right)\mathrm{cm}</math></center> |
| + | También podemos hallar este CIr empleando la fórmula | ||
| + | <center><math>\overrightarrow{OI}_{21}=\frac{\omega_{20}\overrightarrow{OI}_{20}+\omega_{01}\overrightarrow{OI}_{01}}{\omega_{20}+\omega_{01}}</math></center> | ||
| + | |||
| + | que para este caso nos da | ||
| + | |||
| + | <center><math>\overrightarrow{OI}_{21}=\frac{-6.00(100\vec{\jmath}_3)+2.25(100\vec{\imath}_3)}{-6.00+2.25}\,\mathrm{cm}=\left(-60\vec{\imath}_3+160\vec{\jmath}_3\right)\mathrm{cm}</math></center> | ||
| + | |||
| + | Alternativamente, este CIR puede obtenerse gráficamente. Por el teorema de los tres centros, el CIR <math>I_{21}</math> se encuentra alineado con los dos centros <math>I_{20}</math> e <math>I_{10}</math>. Por tanto, se encuentra sobre una recta que pasa por A y B. Asimismo, se encuentra alineado con los centros <math>I_{32}</math> e <math>I_{31}</math>. Por ello, pertenece también a la recta que pasa por C y D. El CIR buscado se encuentra entonces en la intersección de estas dos rectas, la que pasa por AB y la que pasa por C y D. | ||
| + | |||
| + | Algebraicamente, esto se expresa observando que el vector <math>\overrightarrow{CI}</math> debe ser proporcional al <math>\overrightarrow{CD}</math> | ||
| + | |||
| + | <center><math>\overrightarrow{CI}_{21}=\lambda\overrightarrow{CD}=\lambda\left(-60\vec{\imath}_3+80\vec{\jmath}_3\right)\,\mathrm{cm}</math></center> | ||
| + | |||
| + | y el <math>\overrightarrow{AI}_{21}</math> al <math>\overrightarrow{AB}</math> | ||
| + | |||
| + | <center><math>\overrightarrow{AI}_{21}\times\overrightarrow{AB}=\vec{0}</math></center> | ||
| + | |||
| + | Sustituyendo tenemos | ||
| + | |||
| + | <center><math>\overrightarrow{AI}_{21}=\overrightarrow{AC}+\overrightarrow{CI}_{21}=\left((-40-60\lambda)\vec{\imath}_3+80\lambda\vec{\jmath}_3\right)\mathrm{cm}</math></center> | ||
| + | |||
| + | Hallamos el producto vectorial y lo igualamos a cero | ||
| + | |||
| + | <center><math>\vec{0}=\overrightarrow{AI}_{21}\times\overrightarrow{AB}=\left|\begin{matrix}\vec{\imath}_3 & \vec{\jmath}_3 & \vec{k} \\ | ||
| + | -40-60\lambda & 80\lambda & 0 \\ -100 & 100 & 0\end{matrix}\right|\,\mathrm{cm}^2 = 100(-40+20\lambda)\vec{k}\,\mathrm{cm}^2</math></center> | ||
| + | |||
| + | de donde | ||
| + | |||
| + | <center><math>\lambda = 2\,</math>{{tose}}<math>\overrightarrow{CI}_{21}=\left(-120\vec{\imath}_3+160\vec{\jmath}_3\right)\,\mathrm{cm}</math></center> | ||
| + | |||
| + | y respecto al centro del aro | ||
| + | |||
| + | <center><math>\overrightarrow{OI}_{21}=\overrightarrow{OC}+\overrightarrow{CI}_{21}=\left(-60\vec{\imath}_3+160\vec{\jmath}_3\right)\,\mathrm{cm}</math></center> | ||
| + | |||
| + | |||
| + | <center>[[Archivo:dos-discos-aro-reticula.png]]</center> | ||
| + | |||
| + | Igualmente, puede verificarse que se encuentran alineados los centros <math>I_{30}</math>, <math>I_{31}</math> e <math>I_{10}</math>, por un lado (los tres están en el eje <math>OX_3</math>) y los centros <math>I_{30}</math>, <math>I_{32}</math> e <math>I_{20}</math> por otro (sobre el eje <math>OY_3</math>). | ||
| + | |||
| + | Cuando las discos van avanzando sobre el aro, los seis centros van girando respecto al aro, manteniendo una posición fija respecto al sólido “3”. | ||
| + | |||
| + | <!-- | ||
[[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | [[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | ||
| + | --> | ||
última version al 14:22 11 nov 2012
Contenido |
1 Enunciado
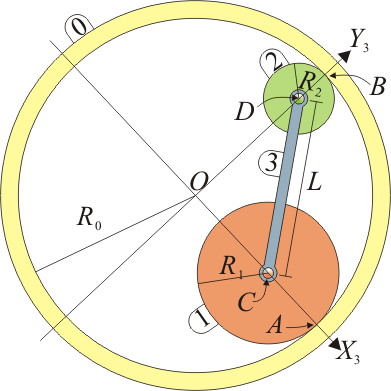
Se tiene el sistema de la figura, formado por dos discos “1” y “2” de radios 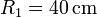 y
y 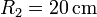 cuyos centros, C y D, están unidos por una barra rígida “3” de longitud
cuyos centros, C y D, están unidos por una barra rígida “3” de longitud 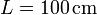 . Las dos ruedas del artilugio ruedan sin deslizar por la superficie interior de un aro “0” de radio
. Las dos ruedas del artilugio ruedan sin deslizar por la superficie interior de un aro “0” de radio 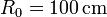 , siendo A y B los respectivos puntos de contacto. El centro del disco “1” gira con velocidad angular constante
, siendo A y B los respectivos puntos de contacto. El centro del disco “1” gira con velocidad angular constante 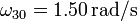 en sentido antihorario respecto al aro exterior “0”.
en sentido antihorario respecto al aro exterior “0”.
- Determine las cinco velocidades angulares relativas restantes.
- Localice los seis centros instantáneos de rotación.
Sugerencia: Emplee el sistema de ejes ligado al sólido “3” de la figura, tal que el eje OX3 pasa por el centro del disco “1”.
2 Velocidad angulares
2.1 Movimiento {30}
El enunciado nos da la velocidad angular con la que gira el punto C, centro del disco 1 alrededor del centro del aro “0”. Este punto pertenece tanto al sólido “1” como al “3” por tratarse de la articulación de la barra con el disco. Esta velocidad angular es la que posee toda la barra “3” en su rotación alrededor de O. Por eso, los subíndices del dato se refieren al movimiento {30} (y no al {10} ya que como veremos, el disco 1 posee una velocidad angular diferente):
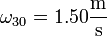
2.2 Movimiento {10}
Para hallar la velocidad angular observamos que este movimiento es una rotación alrededor del punto de contacto, A, y por tanto la velocidad del centro del disco “1” en este movimiento es

Por otro lado tenemos que la velocidad de C, considerado como parte de “3”, es una rotación alrededor de O
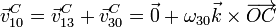
Igualando ambas velocidades llegamos a la relación
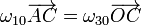
Los vectores de posición relativos valen, en el sistema de referencia indicado:
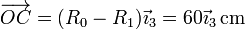
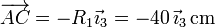
De aquí obtenemos la velocidad angular
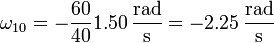
2.3 Movimiento {31}
La velocidad angular del movimiento {31} es inmediata por aplicación de la ley de composición correspondiente

2.4 Movimiento {20}
El punto D, centro del disco “2” también gira alrededor de O con la misma velocidad angular que C. Considerado como parte del sólido “3” su velocidad lineal es
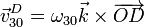
mientras que, considerado como parte del disco “2” realiza una rotación instantánea alrededor del punto B, de contacto del disco con el aro.
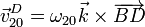
Estas dos velocidades deben ser iguales, ya que

Sustituyendo, llegamos a la relación
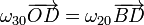
Aunque para determinar la velocidad angular nos basta con saber que los vectores de posición son proporcionales y de sentido opuesto, vamos a determinar su expresión en el sistema de referencia indicado, ya que ésta puede ser útil más adelante.
La figura sugiere que los puntos B y D se encuentran sobre el eje OY3. Sin embargo, no tenemos certeza de tal afirmación. De hecho, para valores arbitrarios de R1, R2 y L no será cierto en general. Vamos a demostrar que sí ocurre para los datos del enunciado. Para ello, hemos de probar que el ángulo COD es recto.
En el triángulo OCD los lados valen
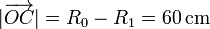
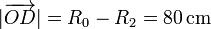
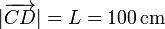
Aplicando el teorema del coseno tenemos que si γ es el ángulo en O
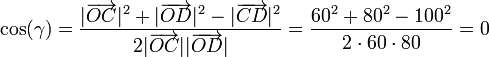
Por tanto el ángulo es efectivamente recto y los vectores de posición relativos son
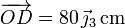
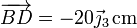
y la velocidad angular del movimiento {20} valen
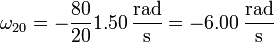
2.5 Movimiento {32}
De nuevo empleamos la ley de composición de velocidades angulares para hallar la del movimiento {32}
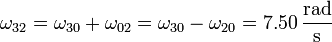
2.6 Movimiento {21}
Por último, para hallar la velocidad angular con la que gira un disco respecto al otro empleamos de nuevo la ley de composición de velocidades empleando el aro “0” como sólido intermedio
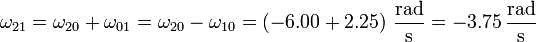
Alternativamente, podemos emplear la barra “3” como sólido intermedio

3 Centros instantáneos de rotación
La mayoría de los centros instantáneos de rotación son inmediatos. De hecho, todos menos uno.
- Movimiento {30}
- El movimiento de la barra “3” respecto al aro “0” es una rotación alrededor del centro de éste. Por tanto
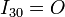
- En forma vectorial
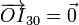
- Movimiento {13}
- Respecto de la barra “3”, el disco “1” realiza una rotación alrededor de su centro, por lo que
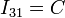
- En forma vectorial
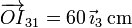
- Movimiento {23}
- Análogamente, el disco “2” ejecuta, respecto de la barra “3”, una rotación alrededor de su centro:
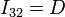
- En forma vectorial
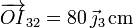
- Movimiento {10}
- Dado que el contacto entre el disco 1 y el aro 0 implica rodadura sin deslizamiento, el CIR del movimiento es el punto de contacto

- En forma vectorial
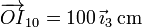
- Movimiento {20}
- El disco “2” también realiza, respecto del aro “0”, una rotación instantánea alrededor del punto de contacto, por lo que
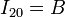
- En forma vectorial
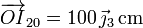
- Movimiento {21}
- Este es el único que no es evidente. Podemos hallar este punto analítica y gráficamente. Para calcularlo de manera analítica precisamos la velocidad de un punto. Si queremos la posición respecto al punto O, la fórmula correspondiente es
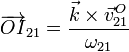
- Necesitamos la velocidad del punto O en el movimiento {21}. La obtenemos aplicando la fórmula de composición de velocidades. Los movimientos {20} y {10} son rotaciones instantáneas alrededor de los puntos B y A por lo que
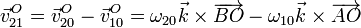
- Sustituyendo los valores numéricos
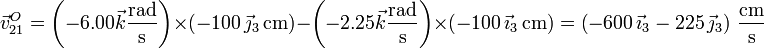
- Llevando esto a la expresión analítica del CIR nos queda
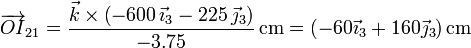
También podemos hallar este CIr empleando la fórmula
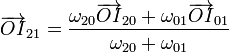
que para este caso nos da
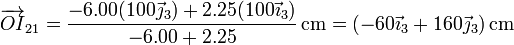
Alternativamente, este CIR puede obtenerse gráficamente. Por el teorema de los tres centros, el CIR I21 se encuentra alineado con los dos centros I20 e I10. Por tanto, se encuentra sobre una recta que pasa por A y B. Asimismo, se encuentra alineado con los centros I32 e I31. Por ello, pertenece también a la recta que pasa por C y D. El CIR buscado se encuentra entonces en la intersección de estas dos rectas, la que pasa por AB y la que pasa por C y D.
Algebraicamente, esto se expresa observando que el vector 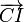 debe ser proporcional al
debe ser proporcional al 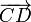
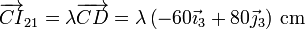
y el 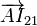 al
al 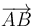
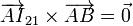
Sustituyendo tenemos
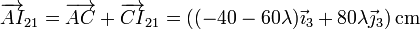
Hallamos el producto vectorial y lo igualamos a cero
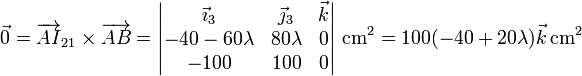
de donde
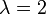

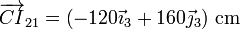
y respecto al centro del aro
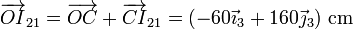
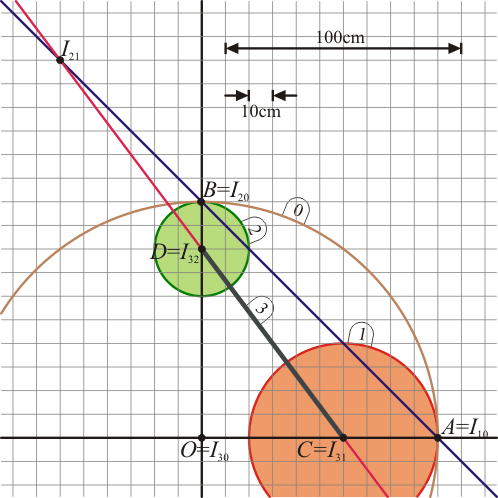
Igualmente, puede verificarse que se encuentran alineados los centros I30, I31 e I10, por un lado (los tres están en el eje OX3) y los centros I30, I32 e I20 por otro (sobre el eje OY3).
Cuando las discos van avanzando sobre el aro, los seis centros van girando respecto al aro, manteniendo una posición fija respecto al sólido “3”.





